2023年山东省滨州市阳信县+中考模拟数学训练试题(含答案)

这是一份2023年山东省滨州市阳信县+中考模拟数学训练试题(含答案)，共9页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
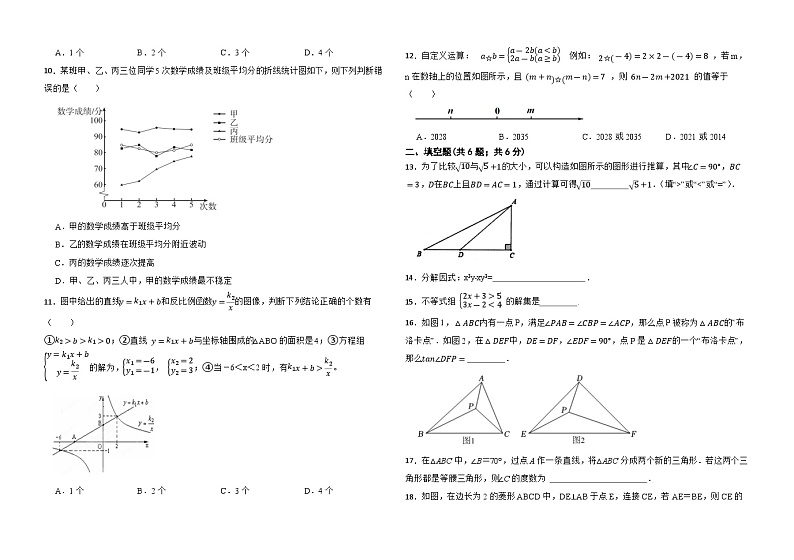
 山东省滨州市阳信县2023年中考模拟数学训练试题一、单选题(共12题；共24分)1．下列各数中，既不是正数也不是负数的是(　　)   A．0 B．－（－1） C．－  D．22．已知a＞b，则下列不等关系中正确的是（　　）   A．ac＞bc B．a＋c2＞b＋c2 C．a－1＞b＋1 D．ac2＞bc23．计算y2（﹣xy3）2的结果是（　　）A．x3y10 B．x2y8 C．﹣x3y8 D．x4y124．已知   是二元一次方程 的解，则2m-n的算术平方根为（　　）A．±2 B．2 C． D．45．如图，在⊙O中，弦AC∥半径OB，∠BOC=50°，则∠OAB的度数为（　　）  A．25° B．50° C．60° D．30°6．如图，PA，PB是⊙O的切线，A，B是切点，点C为⊙O上一点，若∠ACB＝70°，则∠P的度数为（　　） A．70° B．50° C．20° D．40°7．已知关于x的方程x2﹣2（a﹣1）x+a2﹣a﹣2＝0有两个不相等的实数根x1，x2，且x1，x2满足，则a的值为（　　）A．6 B．﹣1 C．6或﹣1 D．1或﹣68．已知□AOCD的顶点，点C在x轴的正半轴上，现按以下步骤作图：①以点O为圆心，适当长为半径画弧，分别交OA于点M，交OC于点N.②分别以点M，N为圆心，大于的长为半径画弧，两弧在内相交于点E.③画射线OE，交AD于点，则点A的横坐标为（　　）A． B． C． D．9．抛物线 的部分图象如图所示，与x轴的一个交点坐标为 ，抛物线的对称轴是 .下列结论中：① ；② ；③ ；④若点 在该抛物线上，则 .其中正确的有（　　） A．1个 B．2个 C．3个 D．4个10．某班甲、乙、丙三位同学5次数学成绩及班级平均分的折线统计图如下，则下列判断错误的是（　　）A．甲的数学成绩高于班级平均分B．乙的数学成绩在班级平均分附近波动C．丙的数学成绩逐次提高D．甲、乙、丙三人中，甲的数学成绩最不稳定11．图中给出的直线和反比例函数的图像，判断下列结论正确的个数有（　　）
①；②直线 与坐标轴围成的△ABO的面积是4；③方程组的解为，， ；④当－6＜x＜2时，有。
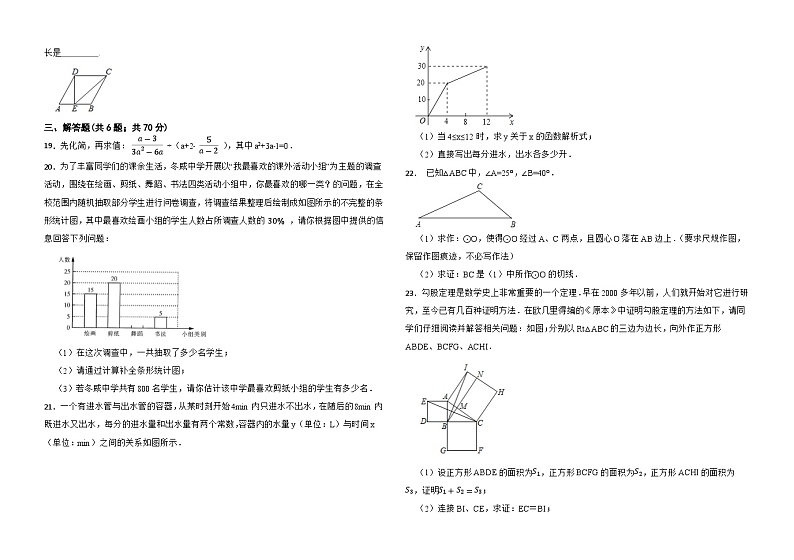
 A．1个 B．2个 C．3个 D．4个12．自定义运算：    例如： ，若m，n在数轴上的位置如图所示，且 ，则 的值等于（　　）  A．2028 B．2035 C．2028或2035 D．2021或2014二、填空题(共6题；共6分)13．为了比较与的大小，可以构造如图所示的图形进行推算，其中，，在上且，通过计算可得　     　．（填“>”或“<”或“=”）．14．分解因式：x3y﹣xy3=　                  　．15．不等式组 的解集是　     　.   16．如图1，内有一点P，满足，那么点P被称为的“布洛卡点”．如图2，在中，，，点P是的一个“布洛卡点”，那么　     　．17．在△ABC中，∠B＝70°，过点A作一条直线，将△ABC分成两个新的三角形．若这两个三角形都是等腰三角形，则∠C的度数为 　                   　．18．如图，在边长为2的菱形ABCD中，DE⊥AB于点E，连接CE，若AE＝BE，则CE的长是　     　.三、解答题(共6题；共70分)19．先化简，再求值： ÷（a+2﹣ ），其中a2+3a﹣1=0．  20．为了丰富同学们的课余生活，冬威中学开展以“我最喜欢的课外活动小组”为主题的调查活动，围绕在绘画、剪纸、舞蹈、书法四类活动小组中，你最喜欢的哪一类？的问题，在全校范围内随机抽取部分学生进行问卷调查，将调查结果整理后绘制成如图所示的不完整的条形统计图，其中最喜欢绘画小组的学生人数占所调查人数的 ，请你根据图中提供的信息回答下列问题：  （1）在这次调查中，一共抽取了多少名学生；   （2）请通过计算补全条形统计图；   （3）若冬威中学共有800名学生，请你估计该中学最喜欢剪纸小组的学生有多少名．   21．一个有进水管与出水管的容器，从某时刻开始4min内只进水不出水，在随后的8min内既进水又出水，每分的进水量和出水量有两个常数，容器内的水量y（单位：L）与时间x（单位：min）之间的关系如图所示．​（1）当4≤x≤12时，求y关于x的函数解析式；（2）直接写出每分进水，出水各多少升．22． 已知△ABC中，∠A=25°，∠B=40°．  （1）求作：⊙O，使得⊙O经过A、C两点，且圆心O落在AB边上．（要求尺规作图，保留作图痕迹，不必写作法）  （2）求证：BC是（1）中所作⊙O的切线．  23．勾股定理是数学史上非常重要的一个定理．早在2000多年以前，人们就开始对它进行研究，至今已有几百种证明方法．在欧几里得编的《原本》中证明勾股定理的方法如下，请同学们仔细阅读并解答相关问题：如图；分别以Rt△ABC的三边为边长，向外作正方形ABDE、BCFG、ACHI．（1）设正方形ABDE的面积为，正方形BCFG的面积为，正方形ACHI的面积为，证明；（2）连接BI、CE，求证：EC＝BI；（3）过点B作AC的垂线，交AC于点M，交IH于点N．试说明四边形AMNI与正方形ABDE的面积相等．24．如图，抛物线 与x轴交于A、B两点，与y轴交于点C，已知A（–1，0），且直线BC的解析式为y= x-2，作垂直于x轴的直线 ，与抛物线交于点F，与线段BC交于点E（不与点B和点C重合）.  （1）求抛物线的解析式；   （2）若△CEF是以CE为腰的等腰三角形，求m的值；   （3）点P为y轴左侧抛物线上的一点，过点P作 交直线BC于点M，连接PB，若以P、M、B为顶点的三角形与△ABC相似，求P点的坐标.  
答案解析部分1．【答案】A2．【答案】B3．【答案】B4．【答案】B5．【答案】A6．【答案】D7．【答案】B8．【答案】D9．【答案】D10．【答案】D11．【答案】C12．【答案】B13．【答案】＜14．【答案】xy（x+y）（x﹣y）15．【答案】16．【答案】17．【答案】20°或27.5°或35°18．【答案】19．【答案】解： ÷（a+2﹣ ）  = = = ，∵a2+3a﹣1=0，∴a2+3a=1，∴3a2+9a=3，故原式= ．20．【答案】（1）解：15÷30%＝50（名），  答：本次调查共抽取了50名学生；（2）解：50﹣15﹣20﹣5＝10（名），  补全条形统计图如图所示：（3）解：800× ＝320（名），   答：估计该中学最喜欢剪纸小组的学生有320名．21．【答案】（1）解：（1）设当4≤x≤12时的直线方程为：y=kx+b（k≠0）．∵图象过（4，20）、（12，30），∴30，解得：，∴y=x+15 （4≤x≤12）；（2）解：根据图象，每分钟进水20÷4=5升，设每分钟出水m升，则 5×8﹣8m=30﹣20，解得：m=．故每分钟进水、出水各是5升、升．22．【答案】（1）解：作图如图1：  （2）证明：如图2，  连接OC，∵OA=OC，∠A=25°∴∠BOC=50°，又∵∠B=40°，∴∠BOC+∠B=90°∴∠OCB=90°∴OC⊥BC∴BC是⊙O的切线．23．【答案】（1）证明：在中，由勾股定理得：，，，，（2）证明：四边形、四边形是正方形，，，，，在和中，，，；（3）证明：，，，四边形的面积的面积，同理：正方形的面积的面积，又，四边形与正方形的面积相等．24．【答案】（1）解：由题意得： 将y=0代入y= x-2中，得x=4∴点B的坐标为（4,0）将A（-1，0），B（4，0）代入 得 ，解得， （2）解： ∴（i）若以C为等腰三角形的顶点，则CE2=CF2∴解得：m1=2，m2=4（不符合前提条件，故舍去）；（ii）若以E为等腰三角形的顶点，则EC2=EF2∴解得： （不符合前提条件，故舍去）；综上：m=2或 （3）解：①根据勾股定理可得：AC= = ，BC= = ，AB=5   ∴AC2+BC2=25=AB2，∴△ABC为直角三角形，∠ACB=90°∴当点P与点A重合时，点M与点C重合，此时P1（-1，0），②如图，当△BPM∽△ABC时，∴∠BPM=∠ABC过点M作HR∥x轴，作PH⊥HR于点H，BR⊥HR与点R，∴∠PHM=∠MRB=∠PMB=90°∴∠HPM＋∠PMH=90°，∠RMB＋∠PMH=90°∴∠HPM=∠RMB∴△PHM∽△MRB∴又∵AB//HR∴∴令BR=a，MR=2a又∵∴∴∴PH=4a，HM=2a，PQ=3a，又∵点P在抛物线上，将 代入 整理，得 解得： （舍）， ∴∴符合条件的点P为P1（-1，0）或