中考数学二轮复习重难点复习题型04 多边形证明 类型一 三角形全等与相似（专题训练）（2份打包，原卷版+解析版）

题型四 多边形证明

类型一 三角形全等与相似（专题训练）

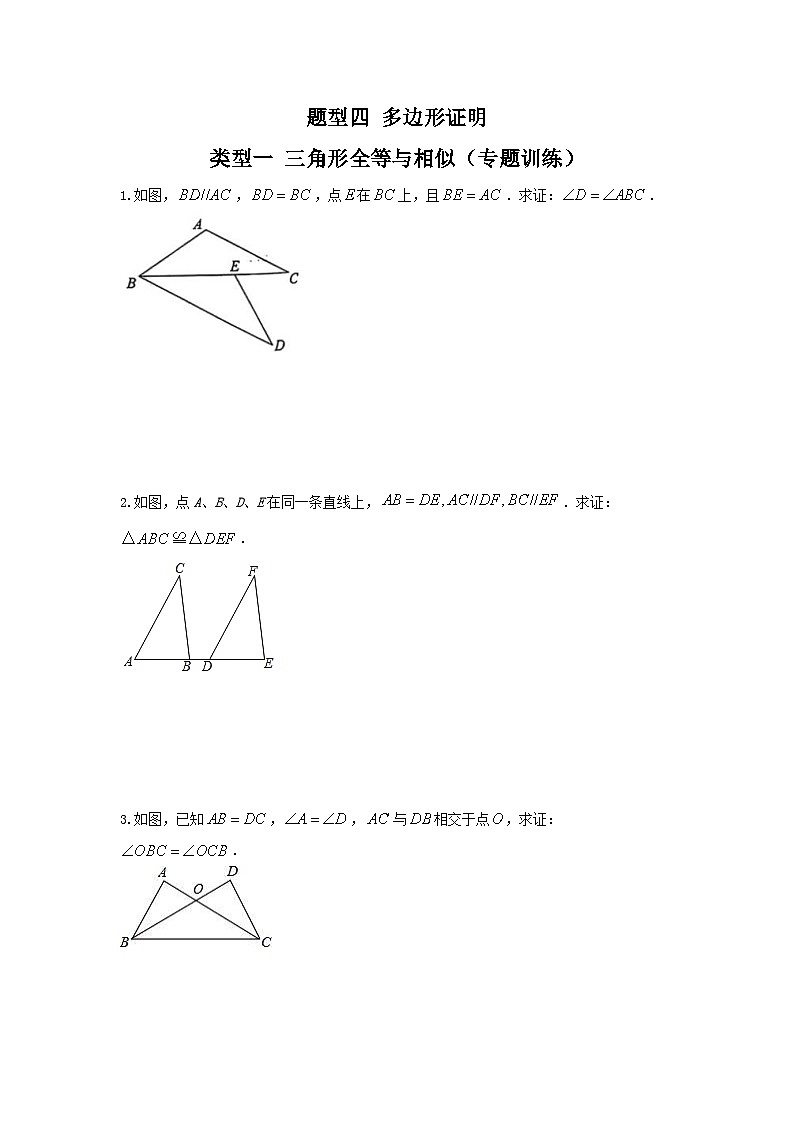
1.如图，，，点在上，且．求证：．

【答案】见解析

【分析】

由题意易得，进而可证，然后问题可求证．

【详解】

证明：∵，

∴．

∵，，

∴．

∴．

【点睛】

本题主要考查全等三角形的性质与判定，熟练掌握全等三角形的性质与判定是解题的关键．

2.如图，点A、B、D、E在同一条直线上，．求证：．

【答案】见解析

【分析】

根据，可以得到，然后根据题目中的条件，利用ASA证明△ABC≌△DEF即可．

【详解】

证明：点A，B，C，D，E在一条直线上

∵

∴

在与中

∴

【点睛】

本题重点考查了三角形全等的判定定理，普通两个三角形全等共有四个定理，即AAS、ASA、SAS、SSS，直角三角形可用HL定理，但AAA、SSA，无法证明三角形全等，本题是一道较为简单的题目．

3.如图，已知，，与相交于点，求证：．

【答案】证明见解析

【分析】

根据全等三角形的性质，通过证明，得，结合等腰三角形的性质，即可得到答案．

【详解】

∵，

∴（AAS），

∴，

∴．

【点睛】

本题考查了全等三角形、等腰三角形的知识；解题的关键是熟练掌握全等三角形、等腰三角形的性质，从而完成求解．

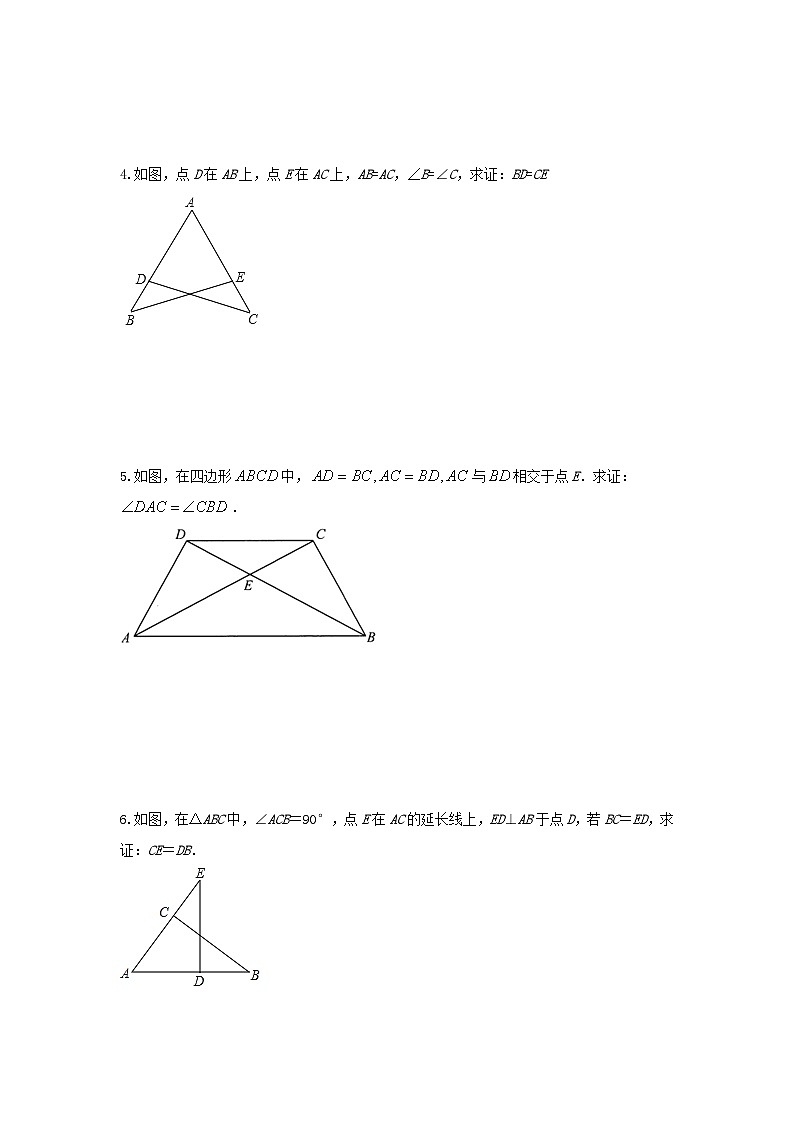
4.如图，点D在AB上，点E在AC上，AB=AC，∠B=∠C，求证：BD=CE

【答案】证明见详解．

【分析】

根据“ASA”证明△ABE≌△ACD，然后根据全等三角形的对应边相等即可得到结论.

【详解】

证明：在△ABE和△ACD中，

∵,

△ABE≌△ACD (ASA)，

∴AE=AD，

∴BD=AB–AD=AC-AE=CE．

【点睛】

本题主要考查全等三角形的判定和性质，掌握全等三角形的判定方法（即SSS、SAS、ASA、AAS和HL）和全等三角形的性质（即全等三角形的对应边相等、对应角相等）是解题的关键．

5.如图，在四边形中，与相交于点E．求证：．

【答案】见解析

【分析】

直接利用SSS证明△ACD≌△BDC，即可证明．

【详解】

解：在△ACD和△BDC中，

，

∴△ACD≌△BDC（SSS），

∴∠DAC=∠CBD．

【点睛】

本题考查了全等三角形的判定和性质，解题的关键是根据题意灵活运用SSS的方法．

6.如图，在△ABC中，∠ACB＝90°，点E在AC的延长线上，ED⊥AB于点D，若BC＝ED，求证：CE＝DB．

【分析】由“AAS”可证△ABC≌△AED，可得AE＝AB，AC＝AD，由线段的和差关系可得结论．

【解答】证明：∵ED⊥AB，

∴∠ADE＝∠ACB＝90°，∠A＝∠A，BC＝DE，

∴△ABC≌△AED（AAS），

∴AE＝AB，AC＝AD，

∴CE＝BD．

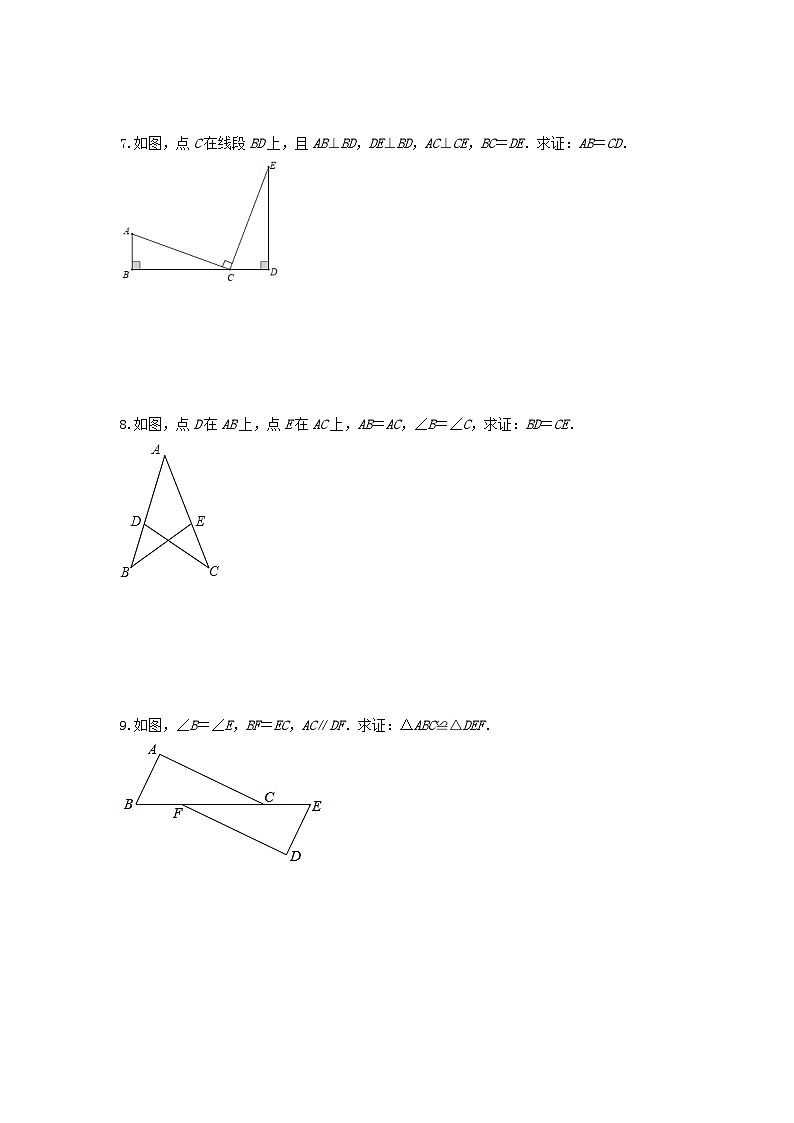
7.如图，点C在线段BD上，且AB⊥BD，DE⊥BD，AC⊥CE，BC＝DE．求证：AB＝CD．

【分析】证明△ABC≌△CDE（ASA），可得出结论．

【解答】证明：∵AB⊥BD，ED⊥BD，AC⊥CE，

∴∠ACE＝∠ABC＝∠CDE＝90°，

∴∠ACB+∠ECD＝90°，∠ECD+∠CED＝90°，

∴∠ACB＝∠CED．

在△ABC和△CDE中，

，

∴△ABC≌△CDE（ASA），

∴AB＝CD．

8.如图，点D在AB上，点E在AC上，AB＝AC，∠B＝∠C，求证：BD＝CE．

【分析】要证BD＝CE只要证明AD＝AE即可，而证明△ABE≌△ACD，则可得AD＝AE．

【解答】证明：在△ABE与△ACD中

，

∴△ABE≌△ACD．

∴AD＝AE．

∴BD＝CE．

9.如图，∠B＝∠E，BF＝EC，AC∥DF．求证：△ABC≌△DEF．

【分析】首先利用平行线的性质得出∠ACB＝∠DFE，进而利用全等三角形的判定定理ASA，进而得出答案．

【解答】证明：∵AC∥DF，

∴∠ACB＝∠DFE，

∵BF＝CE，

∴BC＝EF，

在△ABC和△DEF中，，

∴△ABC≌△DEF（ASA）．

10.如图，AC平分∠BAD，AB＝AD．求证：BC＝DC．

【分析】由“SAS”可证△ABC≌△ADC，可得BC＝DC．

【解答】证明：∵AC平分∠BAD，

∴∠BAC＝∠DAC，

又∵AB＝AD，AC＝AC，

∴△ABC≌△ADC（SAS），

∴BC＝CD．

11.如图，已知AB∥CD，AB＝CD，BE＝CF．

求证：

（1）△ABF≌△DCE；

（2）AF∥DE．

【分析】

（1）先由平行线的性质得∠B＝∠C，从而利用SAS判定△ABF≌△DCE；

（2）根据全等三角形的性质得∠AFB＝∠DEC，由等角的补角相等可得∠AFE＝∠DEF，再由平行线的判定可得结论．

【解答】

证明：（1）∵AB∥CD，

∴∠B＝∠C，

∵BE＝CF，

∴BE﹣EF＝CF﹣EF，

即BF＝CE，

在△ABF和△DCE中，

∵，

∴△ABF≌△DCE（SAS）；

（2）∵△ABF≌△DCE，

∴∠AFB＝∠DEC，

∴∠AFE＝∠DEF，

∴AF∥DE．

12.如图，点C、E、F、B在同一直线上，点A、D在BC异侧，AB∥CD，AE＝DF，∠A＝∠D．

（1）求证：AB＝CD；

（2）若AB＝CF，∠B＝40°，求∠D的度数．

【分析】

（1）根据平行线的性质求出∠B＝∠C，根据AAS推出△ABE≌△DCF，根据全等三角形的性质得出即可；

（2）根据全等得出AB＝CD，BE＝CF，∠B＝∠C，求出CF＝CD，推出∠D＝∠CFD，即可求出答案．

【解答】

（1）证明：∵AB∥CD，

∴∠B＝∠C，

在△ABE和△DCF中，

，

∴△ABE≌△DCF（AAS），

∴AB＝CD；

（2）解：∵△ABE≌△DCF，

∴AB＝CD，BE＝CF，∠B＝∠C，

∵∠B＝40°，

∴∠C＝40°

∵AB＝CF，

∴CF＝CD，

∴∠D＝∠CFD（180°﹣40°）＝70°．

13.已知：如图，点B，D在线段AE上，AD=BE，AC∥EF，∠C=∠F．求证：BC=DF．

【解析】∵AD=BE，

∴AD-BD=BE-BD，

∴AB=ED，

∵AC∥EF，

∴∠A=∠E，

在△ABC和△EDF中，，

∴△ABC≌△EDF（AAS），

∴BC=DF．

14.如图，AB=AD，BC=DC，点E在AC上．

（1）求证：AC平分∠BAD；

（2）求证：BE=DE．

【解析】

（1）在△ABC与△ADC中，

∴△ABC≌△ADC（SSS），

∴∠BAC=∠DAC，

即AC平分∠BAD．

（2）由（1）∠BAE=∠DAE，

在△BAE与△DAE中，得，

∴△BAE≌△DAE（SAS），

∴BE=DE．

15.如图，在△ABC中，AD是BC边上的中线，E是AB边上一点，过点C作CF∥AB交ED的延长线于点F．

（1）求证：△BDE≌△CDF；

（2）当AD⊥BC，AE=1，CF=2时，求AC的长．

【解析】

（1）∵，

∴，

∵是边上的中线，∴，

∴△BDE≌△CDF．

（2）∵△BDE≌△CDF，

∴，

∴．

∵，

∴．

16.如图，是的角平分线，在上取点，使．

（1）求证：．

（2）若，，求的度数．

【答案】（1）见解析；（2）35°

【分析】

（1）直接利用角平分线的定义和等边对等角求出，即可完成求证；
（2）先求出∠ADE，再利用平行线的性质求出∠ ABC，最后利用角平分线的定义即可完成求解．
【详解】

解：（1）平分，

．

，

，

，

．

（2），，

．

．

．

平分，

，

即．

【点睛】

本题综合考查了角平分线的定义、等腰三角形的性质、平行线的判定与性质等内容，解决本题的关键是牢记概念与性质，本题的解题思路较明显，属于几何中的基础题型，着重考查了学生对基本概念的理解与掌握．

17.如图，在中，，点D，E分別在边AB，AC上，，连结CD，BE．

（1）若，求，的度数．

（2）写出与之间的关系，并说明理由．

【答案】（1）；；（2），见解析

【分析】

（1）利用三角形的内角和定理求出的大小，再利用等腰三角形的性质分别求出，．

（2）利用三角形的内角和定理、三角形外角的性质和等腰三角形的性质，求出用含分别表示，，即可得到两角的关系．

【详解】

（1），，

．

在中，，

，

，

，

．

．

（2），的关系：．

理由如下：设，．

在中，，

，

．

，

在中，，

．

．

．

．

【点睛】

本题主要通过求解角和两角之间的关系，考查三角形的内角和定理、三角形外角的性质和等腰三角形的性质．三角形的内角和等于 ．三角形的外角等于与其不相邻的两个内角之和．等腰三角形等边对等角．

18.如图，已知，，与相交于点，求证：．

【答案】证明见解析

【分析】

根据全等三角形的性质，通过证明，得，结合等腰三角形的性质，即可得到答案．

【详解】

∵，

∴（AAS），

∴，

∴．

【点睛】

本题考查了全等三角形、等腰三角形的知识；解题的关键是熟练掌握全等三角形、等腰三角形的性质，从而完成求解．