中考数学二轮复习重难点复习题型07 函数的基本性质（复习讲义）（2份打包，原卷版+解析版）

这是一份中考数学二轮复习重难点复习题型07 函数的基本性质（复习讲义）（2份打包，原卷版+解析版），文件包含中考数学二轮复习重难点复习题型07函数的基本性质复习讲义解析版doc、中考数学二轮复习重难点复习题型07函数的基本性质复习讲义原卷版doc等2份试卷配套教学资源，其中试卷共38页， 欢迎下载使用。
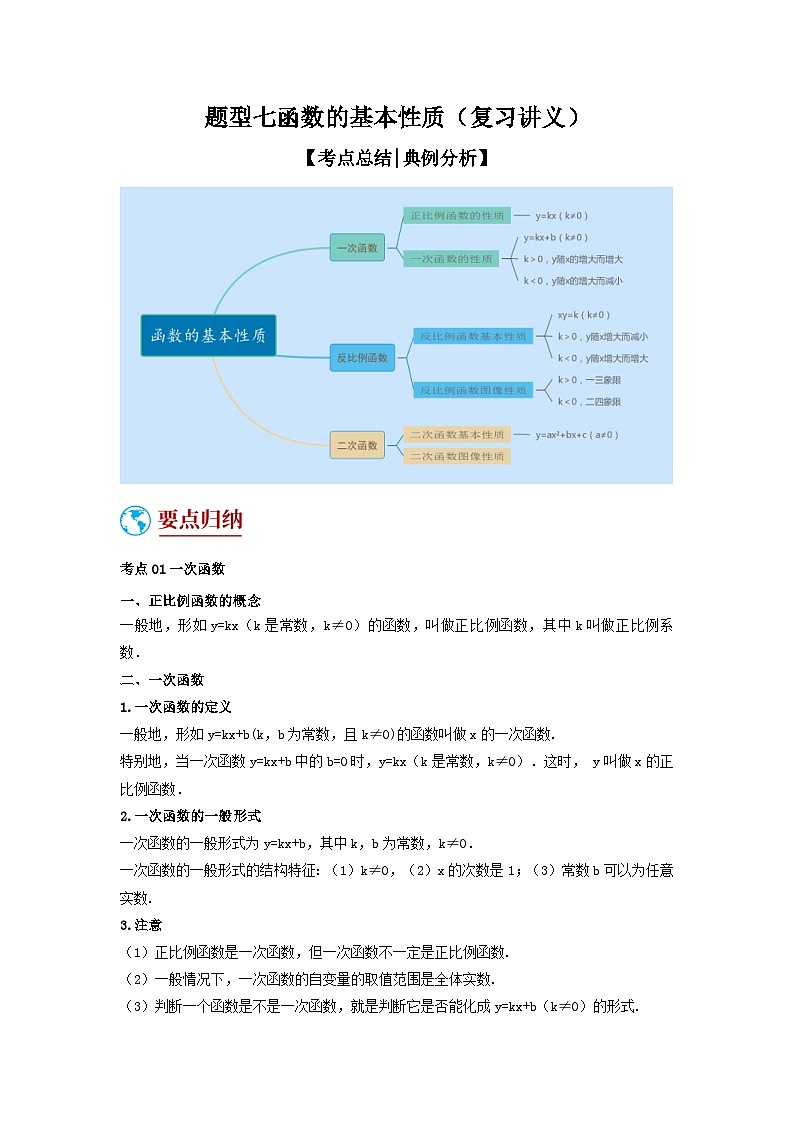
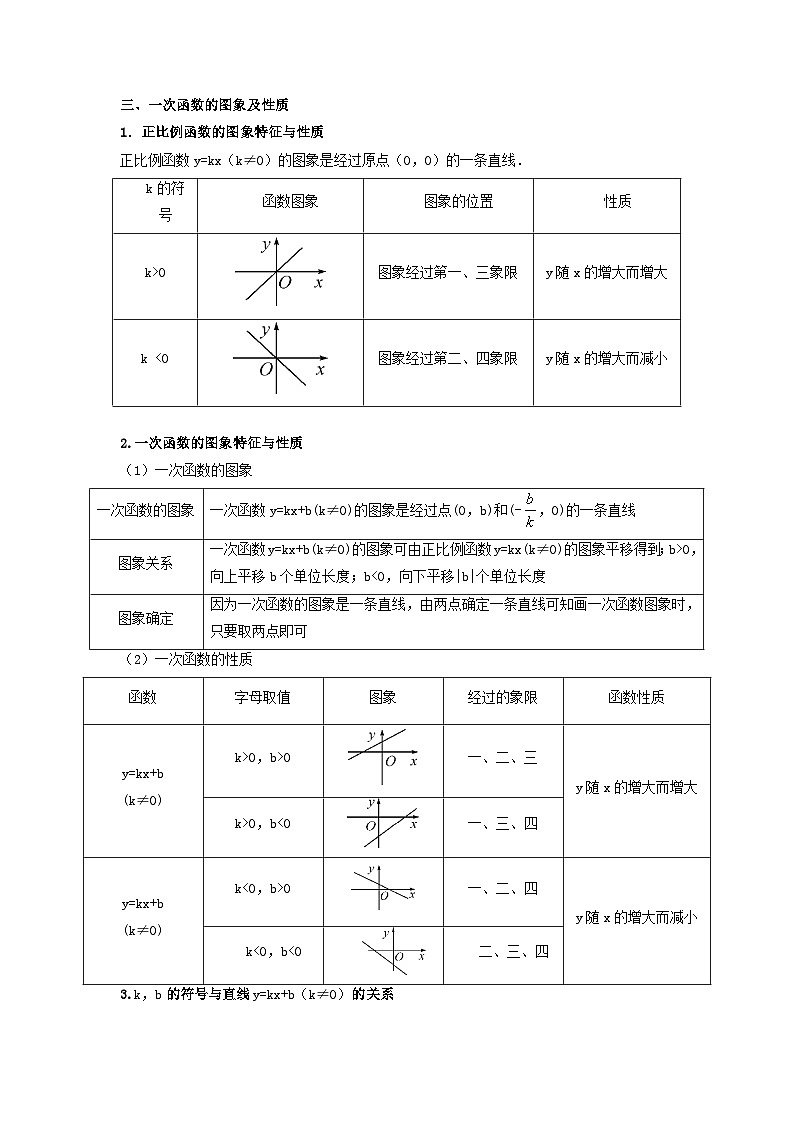
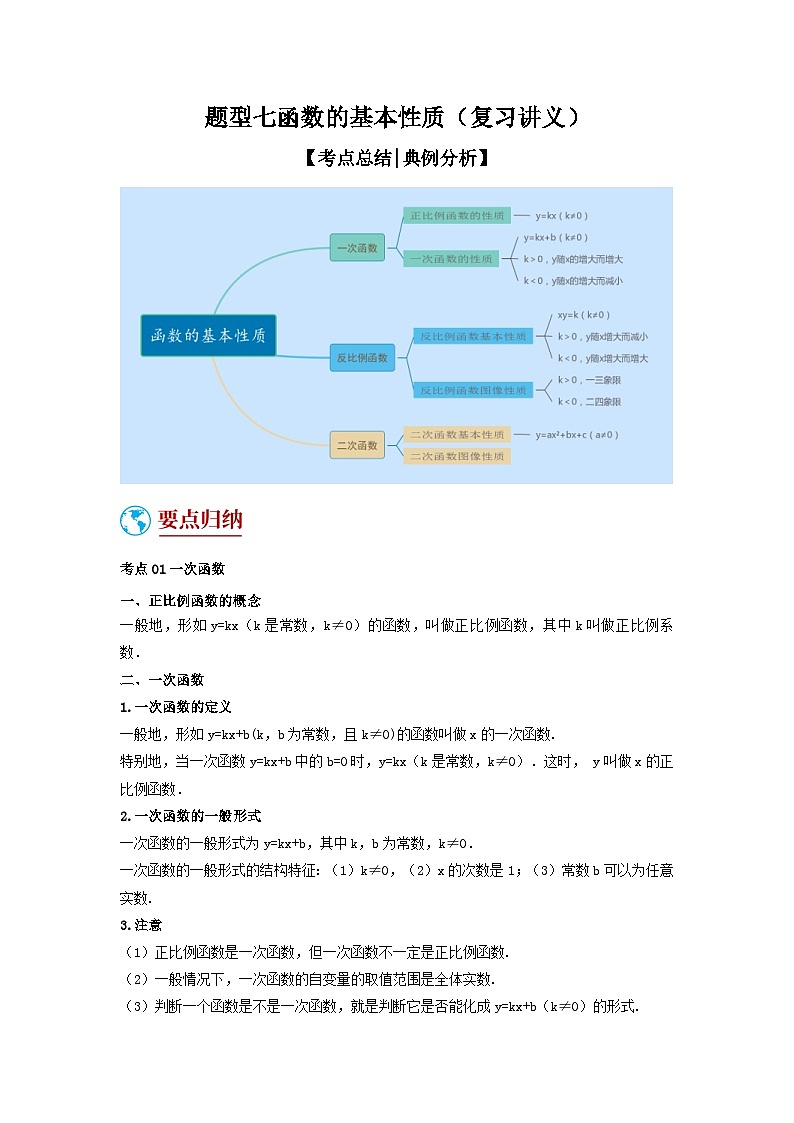
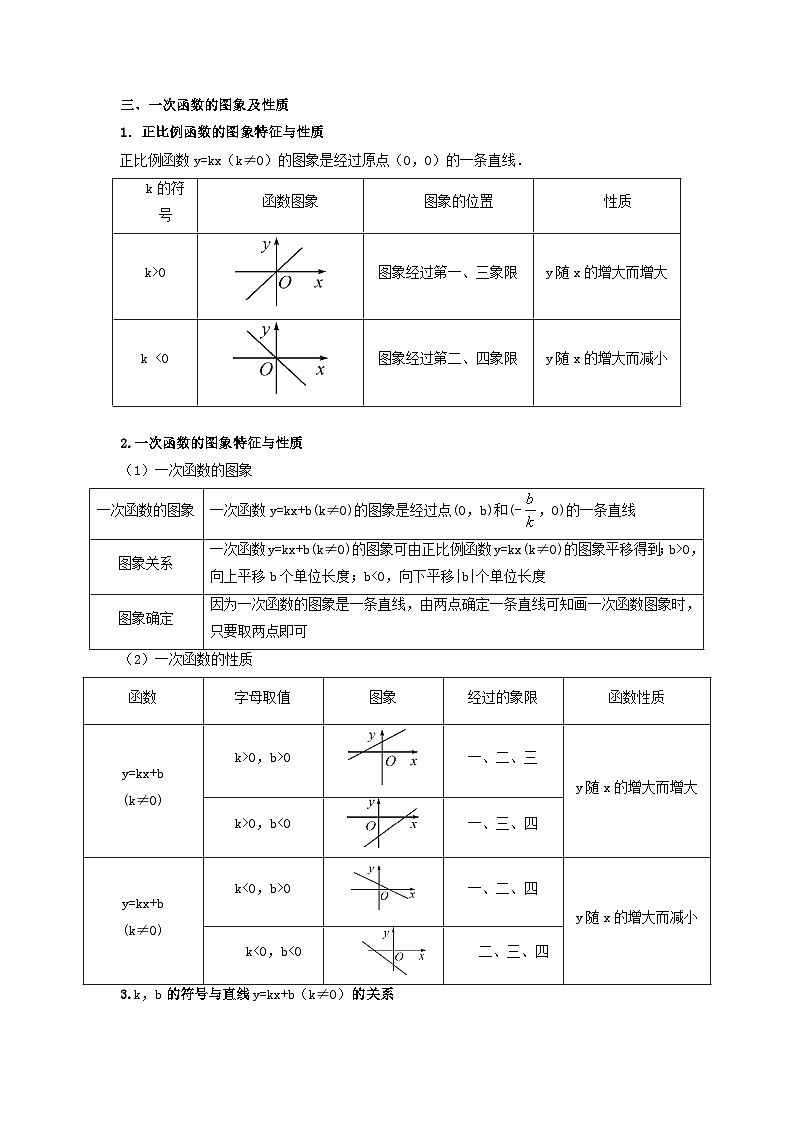
题型七函数的基本性质（复习讲义）【考点总结|典例分析】考点01一次函数一、正比例函数的概念一般地，形如y=kx（k是常数，k≠0）的函数，叫做正比例函数，其中k叫做正比例系数．二、一次函数1.一次函数的定义一般地，形如y=kx+b(k，b为常数，且k≠0)的函数叫做x的一次函数.特别地，当一次函数y=kx+b中的b=0时，y=kx（k是常数，k≠0）．这时， y叫做x的正比例函数．2.一次函数的一般形式一次函数的一般形式为y=kx+b，其中k，b为常数，k≠0．一次函数的一般形式的结构特征：（1）k≠0，（2）x的次数是1；（3）常数b可以为任意实数.3.注意（1）正比例函数是一次函数，但一次函数不一定是正比例函数.（2）一般情况下，一次函数的自变量的取值范围是全体实数.（3）判断一个函数是不是一次函数，就是判断它是否能化成y=kx+b（k≠0）的形式.三、一次函数的图象及性质1．正比例函数的图象特征与性质正比例函数y=kx（k≠0）的图象是经过原点（0，0）的一条直线．k的符号函数图象图象的位置性质k>0图象经过第一、三象限y随x的增大而增大k <0图象经过第二、四象限y随x的增大而减小 2.一次函数的图象特征与性质（1）一次函数的图象一次函数的图象一次函数y=kx+b(k≠0)的图象是经过点(0，b)和(-，0)的一条直线图象关系一次函数y=kx+b(k≠0)的图象可由正比例函数y=kx(k≠0)的图象平移得到；b>0，向上平移b个单位长度；b<0，向下平移|b|个单位长度图象确定因为一次函数的图象是一条直线，由两点确定一条直线可知画一次函数图象时，只要取两点即可（2）一次函数的性质函数字母取值图象经过的象限函数性质y=kx+b(k≠0)k>0，b>0一、二、三y随x的增大而增大k>0，b<0一、三、四y=kx+b(k≠0)k<0，b>0一、二、四y随x的增大而减小k<0，b<0二、三、四3.k，b的符号与直线y=kx+b（k≠0）的关系在直线y=kx+b（k≠0）中，令y=0，则x=- ，即直线y=kx+b与x轴交于（–，0）．①当–>0时，即k，b异号时，直线与x轴交于正半轴．②当–=0，即b=0时，直线经过原点．③当–<0，即k，b同号时，直线与x轴交于负半轴．4.两直线y=k1x+b1（k1≠0）与y=k2x+b2（k2≠0）的位置关系：①当k1=k2，b1≠b2，两直线平行；               ②当k1=k2，b1=b2，两直线重合；③当k1≠k2，b1=b2，两直线交于y轴上一点；     ④当k1·k2=–1时，两直线垂直．四、待定系数法1．定义：先设出函数解析式，再根据条件确定解析式中未知数的系数，从而得出函数解析式的方法叫做待定系数法．2．待定系数法求正比例函数解析式的一般步骤（1）设含有待定系数的函数解析式为y=kx（k≠0）．（2）把已知条件（自变量与函数的对应值）代入解析式，得到关于系数k的一元一次方程．（3）解方程，求出待定系数k．（4）将求得的待定系数k的值代入解析式．3．待定系数法求一次函数解析式的一般步骤（1）设出含有待定系数k、b的函数解析式y=kx+b．（2）把两个已知条件（自变量与函数的对应值）代入解析式，得到关于系数k，b的二元一次方程组．（3）解二元一次方程组，求出k，b．（4）将求得的k，b的值代入解析式．1.已知在平面直角坐标系xOy中，直线y＝2x+2和直线y＝x+2分别交x轴于点A和点B．则下列直线中，与x轴的交点不在线段AB上的直线是（　　）A．y＝x+2 B．y＝x+2 C．y＝4x+2 D．y＝x+2 2.如图，在平面直角坐标系中，直线l1：y=﹣x+1与x轴，y轴分别交于点A和点B，直线l2：y=kx（k≠0）与直线l1在第一象限交于点C．若∠BOC=∠BCO，则k的值为（　　）A． B． C． D．23.如图，在平面直角坐标系中，点A，C分别在x轴、y轴上，四边形ABCO是边长为4的正方形，点D为AB的中点，点P为OB上的一个动点，连接DP，AP，当点P满足DP+AP的值最小时，直线AP的解析式为_____．4.如图，在平面直角坐标系中，直线过点且与轴交于点，把点向左平移2个单位，再向上平移4个单位，得到点.过点且与平行的直线交轴于点.（1）求直线的解析式；（2）直线与交于点，将直线沿方向平移，平移到经过点的位置结束，求直线在平移过程中与轴交点的横坐标的取值范围.    考点02反比例函数一、反比例函数的概念1．反比例函数的概念：一般地，函数（k是常数，k≠0）叫做反比例函数．反比例函数的解析式也可以写成的形式．自变量x的取值范围是x≠0的一切实数，函数的取值范围也是一切非零实数．2．反比例函数（k是常数，k0）中x，y的取值范围自变量x和函数值y的取值范围都是不等于0的任意实数．二、反比例函数的图象和性质1．反比例函数的图象与性质（1）图象：反比例函数的图象是双曲线，它有两个分支，这两个分支分别位于第一、三象限，或第二、四象限．由于反比例函数中自变量x≠0，函数y≠0，所以，它的图象与x轴、y轴都没有交点，即双曲线的两个分支无限接近坐标轴，但永远达不到坐标轴．（2）性质：当k>0时，函数图象的两个分支分别在第一、三象限，在每个象限内，y随x的增大而减小．当k<0时，函数图象的两个分支分别在第二、四象限，在每个象限内，y随x的增大而增大．表达式（k是常数，k≠0）kk>0k<0大致图象所在象限第一、三象限第二、四象限增减性在每个象限内，y随x的增大而减小在每个象限内，y随x的增大而增大2．反比例函数图象的对称性反比例函数的图象既是轴对称图形，又是中心对称图形，其对称轴为直线y=x和y=-x，对称中心为原点．3．注意（1）画反比例函数图象应多取一些点，描点越多，图象越准确，连线时，要注意用平滑的曲线连接各点．（2）随着|x|的增大，双曲线逐渐向坐标轴靠近，但永不与坐标轴相交，因为反比例函数中x≠0且y≠0．（3）反比例函数的图象不是连续的，因此在谈到反比例函数的增减性时，都是在各自象限内的增减情况．当k>0时，在每一象限（第一、三象限）内y随x的增大而减小，但不能笼统地说当k>0时，y随x的增大而减小．同样，当k<0时，也不能笼统地说y随x的增大而增大．三、反比例函数解析式的确定1．待定系数法：确定解析式的方法仍是待定系数法，由于在反比例函数中，只有一个待定系数，因此只需要一对对应值或图象上的一个点的坐标，即可求出k的值，从而确定其解析式．2．待定系数法求反比例函数解析式的一般步骤（1）设反比例函数解析式为（k≠0）；（2）把已知一对x，y的值代入解析式，得到一个关于待定系数k的方程；（3）解这个方程求出待定系数k；（4）将所求得的待定系数k的值代回所设的函数解析式．四、反比例函数中|k|的几何意义1．反比例函数图象中有关图形的面积2．涉及三角形的面积型当一次函数与反比例函数结合时，可通过面积作和或作差的形式来求解．（1）正比例函数与一次函数所围成的三角形面积.如图①，S△ABC=2S△ACO=|k|；（2）如图②，已知一次函数与反比例函数交于A、B两点，且一次函数与x轴交于点C，则S△AOB=S△AOC+S△BOC=+=；（3）如图③，已知反比例函数的图象上的两点，其坐标分别为，，C为AB延长线与x轴的交点，则S△AOB=S△AOC–S△BOC=–=．1.反比例函数经过点，则下列说法错误的是（    ）A． B．函数图象分布在第一、三象限C．当时，随的增大而增大 D．当时，随的增大而减小2.一次函数与反比例函数在同一坐标系中的图象可能是（    ）A． B． C． D．3.如图，平行四边形的顶点在轴的正半轴上，点在对角线上，反比例函数的图像经过、两点．已知平行四边形的面积是，则点的坐标为（  ）A． B． C． D．4.如图，点，点都在反比例函数的图象上，过点分别向轴、轴作垂线，垂足分别为点，．连接，，．若四边形的面积记作，的面积记作，则（    ）A． B． C． D． 5.如图，直线与反比例函数的图象交于A，B两点，已知点A的坐标为，的面积为8．（1）填空：反比例函数的关系式为_________________；（2）求直线的函数关系式；（3）动点P在y轴上运动，当线段与之差最大时，求点P的坐标．6.如图，一次函数的图象与反比例函数的图象相交于，两点．（1）求一次函数和反比例函数的表达式；（2）直线交轴于点，点是轴上的点，若的面积是，求点的坐标．考点03二次函数一、二次函数的概念：一般地，形如y=ax2+bx+c（a，b，c是常数，a≠0）的函数，叫做二次函数．二、二次函数解析式的三种形式（1）一般式：y=ax2+bx+c（a，b，c为常数，a≠0）．（2）顶点式：y=a（x–h）2+k（a，h，k为常数，a≠0），顶点坐标是（h，k）．（3）交点式：y=a（x–x1）（x–x2），其中x1，x2是二次函数与x轴的交点的横坐标，a≠0．三、二次函数的图象及性质1．二次函数的图象与性质解析式二次函数y=ax2+bx+c（a，b，c是常数，a≠0）对称轴x=–顶点（–，）a的符号a>0a<0图象开口方向开口向上开口向下最值当x=–时，y最小值=当x=–时，y最大值=最点抛物线有最低点抛物线有最高点增减性当x<–时，y随x的增大而减小；当x>–时，y随x的增大而增大当x<–时，y随x的增大而增大；当x>–时，y随x的增大而减小2.二次函数图象的特征与a，b，c的关系 字母的符号图象的特征aa>0开口向上a<0开口向下bb=0对称轴为y轴ab>0（a与b同号）对称轴在y轴左侧ab<0（a与b异号）对称轴在y轴右侧cc=0经过原点c>0与y轴正半轴相交c<0与y轴负半轴相交四、抛物线的平移1．将抛物线解析式化成顶点式y=a（x–h） 2+k，顶点坐标为（h，k）． 2．保持y=ax2的形状不变，将其顶点平移到（h，k）处，具体平移方法如下：3．注意二次函数平移遵循“上加下减，左加右减”的原则，据此，可以直接由解析式中常数的加或减求出变化后的解析式；二次函数图象的平移可看作顶点间的平移，可根据顶点之间的平移求出变化后的解析式．五、二次函数与一元二次方程的关系1．二次函数y=ax2+bx+c（a≠0），当y=0时，就变成了一元二次方程ax2+bx+c=0（a≠0）2．ax2+bx+c=0（a≠0）的解是抛物线y=ax2+bx+c（a≠0）的图象与x轴交点的横坐标． （1）b2–4ac>0⇔方程有两个不相等的实数根，抛物线与x轴有两个交点；（2）b2–4ac=0⇔方程有两个相等的实数根，抛物线与x轴有且只有一个交点；（3）b2–4ac<0⇔方程没有实数根，抛物线与x轴没有交点． 1.如图，二次函数y＝ax2+bx+c（a≠0）图象的对称轴为直线x＝﹣1，下列结论：①abc＜0；②3a＜﹣c；③若m为任意实数，则有a﹣bm≤am2+b； ④若图象经过点（﹣3，﹣2），方程ax2+bx+c+2＝0的两根为x1，x2（|x1|＜|x2|），则2x1﹣x2＝5．其中正确的结论的个数是（　　）A．4个 B．3个 C．2个 D．1个2.如图，抛物线y＝ax2+bx+c（a≠0）的对称轴为直线x＝1，与y轴交于点B（0，﹣2），点A（﹣1，m）在抛物线上，则下列结论中错误的是（　　）A．ab＜0           B．一元二次方程ax2+bx+c＝0的正实数根在2和3之间C．a＝       D．点P1（t，y1），P2（t+1，y2）在抛物线上，当实数t＞时，y1＜y23.二次函数y=x2的图象平移后经过点（2，0），则下列平移方法正确的是（　　）A．向左平移2个单位，向下平移2个单位   B．向左平移1个单位，向上平移2个单位C．向右平移1个单位，向下平移1个单位   D．向右平移2个单位，向上平移1个单位4.下列关于二次函数（为常数）的结论，①该函数的图象与函数的图象形状相同；②该函数的图象一定经过点；③当时，y随x的增大而减小；④该函数的图象的顶点在函数的图像上，其中所有正确的结论序号是__________．5.二次函数y＝ax2+bx+c的图象如图所示，下列结论：①ab＞0；②a+b﹣1＝0；③a＞1；④关于x的一元二次方程ax2+bx+c＝0的一个根为1，另一个根为﹣．其中正确结论的序号是_____．  6.已知抛物线．（1）求这条抛物线的对称轴；（2）若该抛物线的顶点在x轴上，求其解析式；     7.已知抛物线与轴有两个不同的交点.(1)求的取值范围；(2)若抛物线经过点和点，试比较与的大小，并说明理由.