中考数学二轮复习重难点复习题型09 二次函数综合题 类型六 二次函数与等腰三角形有关的问题（专题训练）（2份打包，原卷版+解析版）

这是一份中考数学二轮复习重难点复习题型09 二次函数综合题 类型六 二次函数与等腰三角形有关的问题（专题训练）（2份打包，原卷版+解析版），文件包含中考数学二轮复习重难点复习题型09二次函数综合题类型六二次函数与等腰三角形有关的问题专题训练解析版doc、中考数学二轮复习重难点复习题型09二次函数综合题类型六二次函数与等腰三角形有关的问题专题训练原卷版doc等2份试卷配套教学资源，其中试卷共72页， 欢迎下载使用。
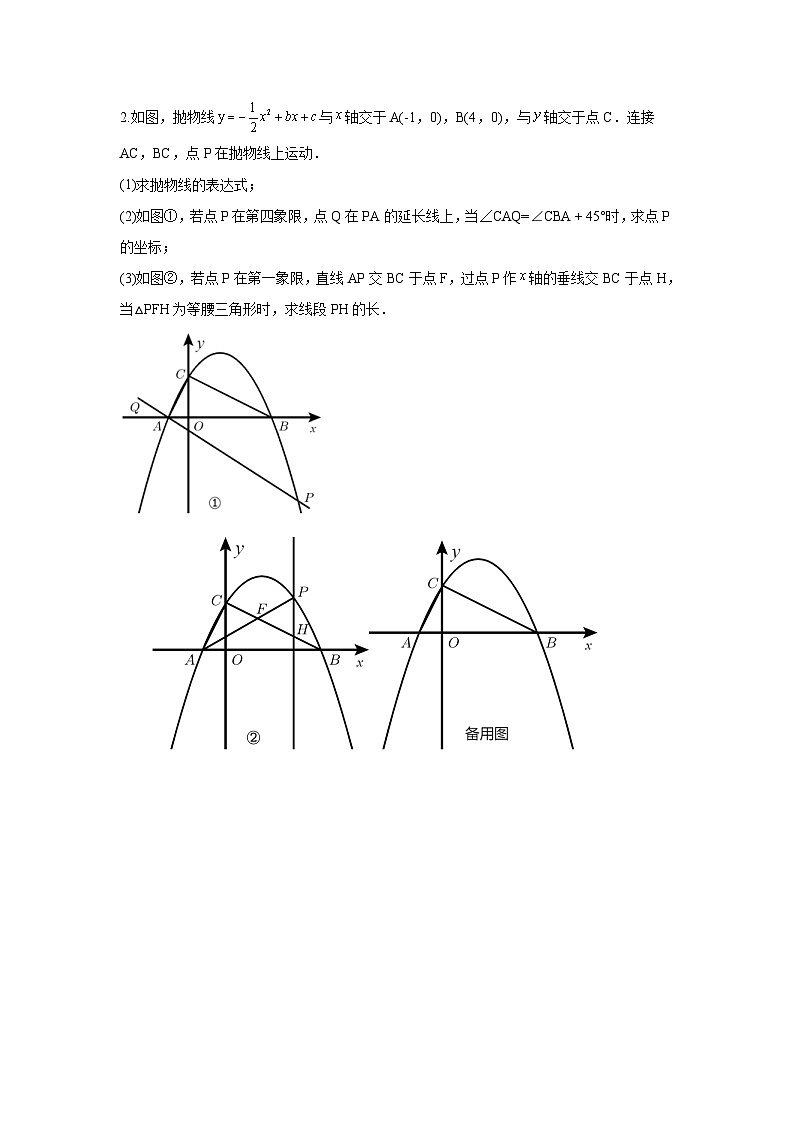
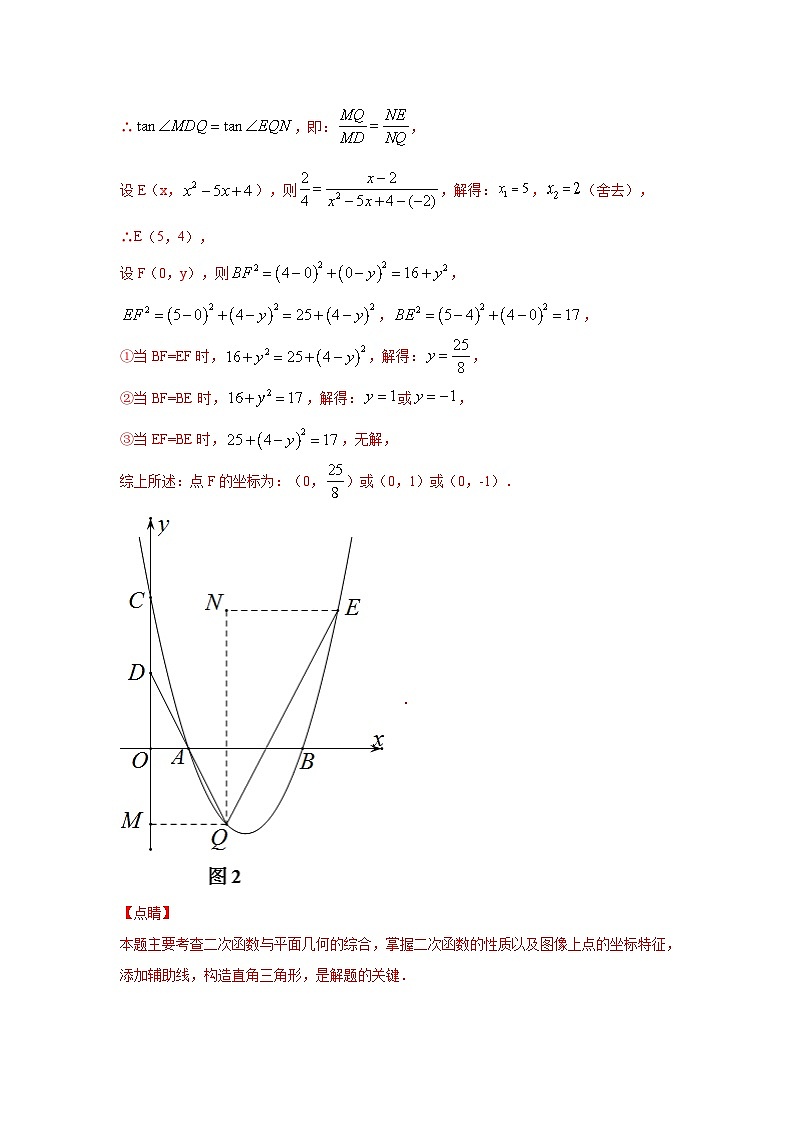
题型九 二次函数综合题 类型六 二次函数与等腰三角形有关的问题（专题训练）1.如图，已知抛物线与x轴交于点A（1，0）和B，与y轴交于点C，对称轴为．（1）求抛物线的解析式；（2）如图1，若点P是线段BC上的一个动点（不与点B，C重合），过点P作y轴的平行线交抛物线于点Q，连接OQ．当线段PQ长度最大时，判断四边形OCPQ的形状并说明理由．（3）如图2，在（2）的条件下，D是OC的中点，过点Q的直线与抛物线交于点E，且．在y轴上是否存在点F，使得为等腰三角形？若存在，求点F的坐标；若不存在，请说明理由．         2.如图，抛物线与轴交于A(-1，0)，B(4，0)，与轴交于点C．连接AC，BC，点P在抛物线上运动．(1)求抛物线的表达式；(2)如图①，若点P在第四象限，点Q在PA的延长线上，当∠CAQ=∠CBA45°时，求点P的坐标；(3)如图②，若点P在第一象限，直线AP交BC于点F，过点P作轴的垂线交BC于点H，当△PFH为等腰三角形时，求线段PH的长．
        3．在平面直角坐标系中，如果一个点的横坐标与纵坐标相等，则称该点为“雁点”．例如……都是“雁点”．（1）求函数图象上的“雁点”坐标；（2）若抛物线上有且只有一个“雁点”E，该抛物线与x轴交于M、N两点（点M在点N的左侧）．当时．①求c的取值范围；②求的度数；（3）如图，抛物线与x轴交于A、B两点（点A在点B的左侧），P是抛物线上一点，连接，以点P为直角顶点，构造等腰，是否存在点P，使点C恰好为“雁点”？若存在，求出点P的坐标；若不存在，请说明理由．        4.（2021·湖南中考真题）如图，已知二次函数的图象经过点且与轴交于原点及点．
（1）求二次函数的表达式；（2）求顶点的坐标及直线的表达式；（3）判断的形状，试说明理由；（4）若点为上的动点，且的半径为，一动点从点出发，以每秒2个单位长度的速度沿线段匀速运动到点，再以每秒1个单位长度的速度沿线段匀速运动到点后停止运动，求点的运动时间的最小值．            5.（2021·黑龙江中考真题）如图，已知抛物线与轴交于点，点，（点在点的左边），与轴交于点，点为抛物线的顶点，连接．直线经过点，且与轴交于点．
（1）求抛物线的解析式；（2）点是抛物线上的一点，当是以为腰的等腰三角形时，求点的坐标；（3）点为线段上的一点，点为线段上的一点，连接，并延长与线段交于点（点在第一象限）．当且时，求出点的坐标．              6.（2020•黔东南州）已知抛物线y＝ax2+bx+c（a≠0）与x轴交于A、B两点（点A在点B的左边），与y轴交于点C（0，﹣3），顶点D的坐标为（1，﹣4）．（1）求抛物线的解析式．（2）在y轴上找一点E，使得△EAC为等腰三角形，请直接写出点E的坐标．（3）点P是x轴上的动点，点Q是抛物线上的动点，是否存在点P、Q，使得以点P、Q、B、D为顶点，BD为一边的四边形是平行四边形？若存在，请求出点P、Q坐标；若不存在，请说明理由．                 7.（2020•枣庄）如图，抛物线y＝ax2+bx+4交x轴于A（﹣3，0），B（4，0）两点，与y轴交于点C，AC，BC．M为线段OB上的一个动点，过点M作PM⊥x轴，交抛物线于点P，交BC于点Q．（1）求抛物线的表达式；（2）过点P作PN⊥BC，垂足为点N．设M点的坐标为M（m，0），请用含m的代数式表示线段PN的长，并求出当m为何值时PN有最大值，最大值是多少？（3）试探究点M在运动过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请求出此时点Q的坐标；若不存在，请说明理由．              8.（2020·内蒙古中考真题）如图，在平面直角坐标系中，抛物线经过坐标原点，与x轴正半轴交于点A，该抛物线的顶点为M，直线经过点A，与y轴交于点B，连接．（1）求b的值及点M的坐标；（2）将直线向下平移，得到过点M的直线，且与x轴负半轴交于点C，取点，连接，求证：：（3）点E是线段上一动点，点F是线段上一动点，连接，线段的延长线与线段交于点G．当时，是否存在点E，使得？若存在，求出点E的坐标；若不存在，请说明理由．  备用图             9.（2020·黑龙江穆棱?朝鲜族学校中考真题）已知抛物线y=a(x－2)2+c经过点A(－2,0)和点C(0,)，与x轴交于另一点B，顶点为D．（1）求抛物线的解析式，并写出顶点D的坐标；（2）如图，点E，F分别在线段AB，BD上（点E不与点A，B重合），且∠DEF=∠DAB，DE=EF，直接写出线段BE的长．   10.（2020·四川内江?中考真题）如图，抛物线经过A（-1，0）、B（4，0）、C（0，2）三点，点D（x，y）为抛物线上第一象限内的一个动点．（1）求抛物线所对应的函数表达式；（2）当的面积为3时，求点D的坐标；（3）过点D作，垂足为点E，是否存在点D，使得中的某个角等于的2倍？若存在，求点D的横坐标；若不存在，请说明理由．   11.（2020·山东潍坊?中考真题）如图，抛物线与x轴交于点和点，与y轴交于点C，顶点为D，连接与抛物线的对称轴l交于点E．（1）求抛物线的表达式；（2）点P是第一象限内抛物线上的动点，连接，当时，求点P的坐标；（3）点N是对称轴l右侧抛物线上的动点，在射线上是否存在点M，使得以点M，N，E为顶点的三角形与相似？若存在，求点M的坐标；若不存在，请说明理由．            12.（2020·湖南湘西?中考真题）已知直线与抛物线（b，c为常数，）的一个交点为，点是x轴正半轴上的动点．（1）当直线与抛物线（b，c为常数，）的另一个交点为该抛物线的顶点E时，求k，b，c的值及抛物线顶点E的坐标；（2）在（1）的条件下，设该抛物线与y轴的交点为C，若点Q在抛物线上，且点Q的横坐标为b，当时，求m的值；（3）点D在抛物线上，且点D的横坐标为，当的最小值多时，求b的值．                  13.（2020·湖南张家界?中考真题）如图，抛物线交x轴于两点，交y轴于点C．直线经过点．（1）求抛物线的解析式；（2）抛物线的对称轴l与直线相交于点P，连接，判定的形状，并说明理由；（3）在直线上是否存在点M，使与直线的夹角等于的2倍？若存在，请求出点M的坐标；若不存在，请说明理由．              14.（2020·湖南岳阳?中考真题）如图1所示，在平面直角坐标系中，抛物线与轴交于点和点，与轴交于点．（1）求抛物线的表达式；（2）如图2，将抛物线先向左平移1个单位，再向下平移3个单位，得到抛物线，若抛物线与抛物线相交于点，连接，，．①求点的坐标；②判断的形状，并说明理由；（3）在（2）的条件下，抛物线上是否存在点，使得为等腰直角三角形，若存在，求出点的坐标；若不存在，请说明理由．           15.（2020·山东枣庄?中考真题）如图，抛物线交x轴于，两点，与y轴交于点C，AC，BC．M为线段OB上的一个动点，过点M作轴，交抛物线于点P，交BC于点Q．（1）求抛物线的表达式；（2）过点P作，垂足为点N．设M点的坐标为，请用含m的代数式表示线段PN的长，并求出当m为何值时PN有最大值，最大值是多少？（3）试探究点M在运动过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形．若存在，请求出此时点Q的坐标；若不存在，请说明理由．