



- 中考数学二轮复习重难点复习题型09 二次函数综合题 类型二 二次函数与线段有关的问题(专题训练)(2份打包,原卷版+解析版) 试卷 2 次下载
- 中考数学二轮复习重难点复习题型09 二次函数综合题 类型六 二次函数与等腰三角形有关的问题(专题训练)(2份打包,原卷版+解析版) 试卷 0 次下载
- 中考数学二轮复习重难点复习题型09 二次函数综合题 类型三 二次函数与面积有关的问题(专题训练)(2份打包,原卷版+解析版) 试卷 0 次下载
- 中考数学二轮复习重难点复习题型09 二次函数综合题 类型十 二次函数与矩形有关的问题(专题训练)(2份打包,原卷版+解析版) 试卷 0 次下载
- 中考数学二轮复习重难点复习题型09 二次函数综合题 类型四 二次函数与角度有关的问题(专题训练)(2份打包,原卷版+解析版) 试卷 0 次下载
中考数学二轮复习重难点复习题型09 二次函数综合题 类型七 二次函数与直角三角形有关的问题(专题训练)(2份打包,原卷版+解析版)
展开题型九 二次函数综合题
类型七 二次函数与直角三角形有关的问题(专题训练)
1.(2022·山东滨州)如图,在平面直角坐标系中,抛物线与x轴相交于点A、B(点A在点B的左侧),与y轴相交于点C,连接.
(1)求线段AC的长;(2)若点Р为该抛物线对称轴上的一个动点,当时,求点P的坐标;
(3)若点M为该抛物线上的一个动点,当为直角三角形时,求点M的坐标.
【答案】(1)(2)(3)或或或
【分析】(1)根据解析式求出A,B,C的坐标,然后用勾股定理求得AC的长;(2)求出对称轴为x=1,设P(1,t),用t表示出PA2和PC2的长度,列出等式求解即可;(3)设点M(m,m2-2m-3),分情况讨论,当,,分别列出等式求解即可.
(1)与x轴交点:
令y=0,解得,
即A(-1,0),B(3,0),
与y轴交点:
令x=0,解得y=-3,
即C(0,-3),
∴AO=1,CO=3,
∴;
(2)抛物线的对称轴为:x=1,
设P(1,t),
∴,,
∴
∴t=-1,
∴P(1,-1);
(3)设点M(m,m2-2m-3),
,
,
,
①当时,
,
解得,(舍),,
∴M(1,-4);
②当时,
,
解得,,(舍),
∴M(-2,5);
③当时,
,
解得,,
∴M或;
综上所述:满足条件的M为或或或.
【点睛】本题是二次函数综合题,考查了与坐标轴交点、线段求值、存在直角三角形等知识,解题的关键是学会分类讨论的思想,属于中考压轴题.
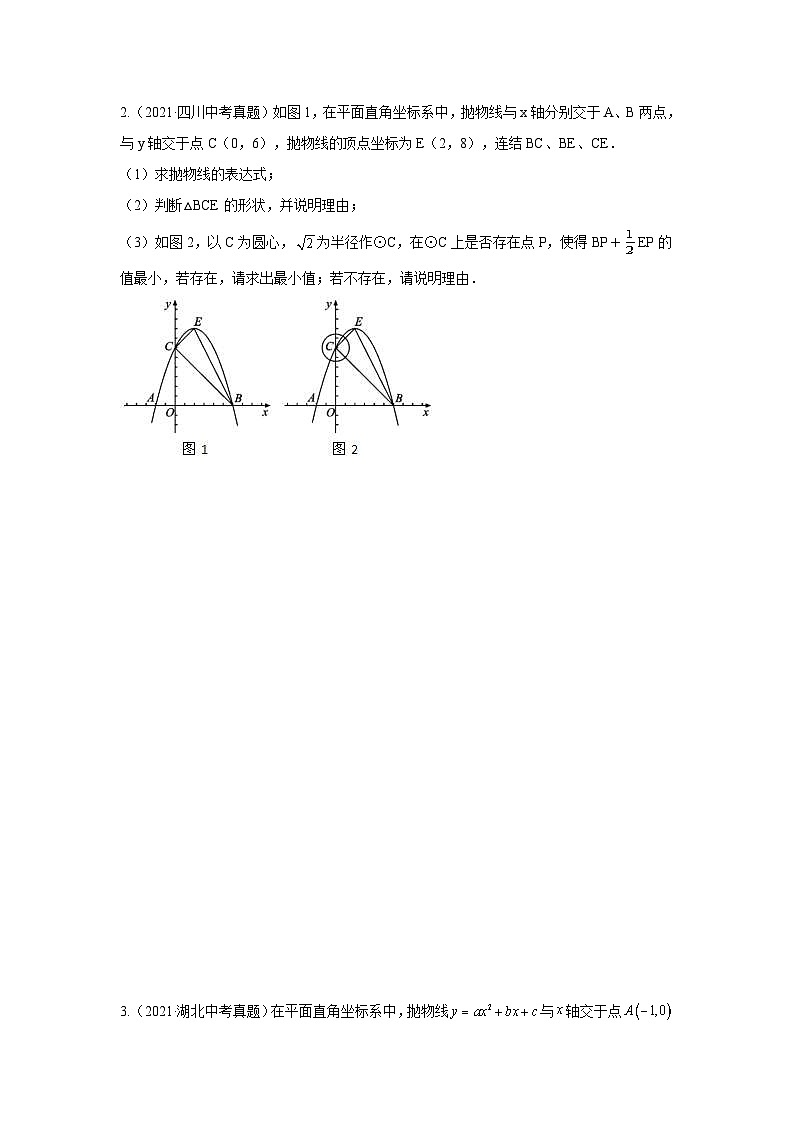
2.(2021·四川中考真题)如图1,在平面直角坐标系中,抛物线与x轴分别交于A、B两点,与y轴交于点C(0,6),抛物线的顶点坐标为E(2,8),连结BC、BE、CE.
(1)求抛物线的表达式;
(2)判断△BCE的形状,并说明理由;
(3)如图2,以C为圆心,为半径作⊙C,在⊙C上是否存在点P,使得BP+EP的值最小,若存在,请求出最小值;若不存在,请说明理由.
【答案】(1)y=x2+2x+6;(2)直角三角形,见解析;(3)存在,
【分析】
(1)用待定系数法求函数解析式;
(2)分别求出三角形三边的平方,然后运用勾股定理逆定理即可证明;
(3)在CE上截取CF=(即CF等于半径的一半),连接BF交⊙C于点P,连接EP,则BF的长即为所求.
【详解】
解:(1)∵抛物线的顶点坐标为E(2,8),
∴设该抛物线的表达式为y=a(x-2)2+8,
∵与y轴交于点C(0,6),
∴把点C(0,6)代入得:a=,
∴该抛物线的表达式为y=x2+2x+6;
(2)△BCE是直角三角形.理由如下:
∵抛物线与x轴分别交于A、B两点,
∴当y=0时,(x-2)2+8=0,解得:x1=-2,x2=6,
∴A(-2,0),B(6,0),
∴BC2=62+62=72,CE2=(8-6)2+22=8,BE2=(6-2)2+82=80,
∴BE2=BC2+CE2,
∴∠BCE=90°,
∴△BCE是直角三角形;
(3)如图,在CE上截取CF=(即CF等于半径的一半),连接BF交⊙C于点P,连接EP,
则BF的长即为所求.
连接CP,∵CP为半径,
∴ ,
又∵∠FCP=∠PCE,
∴△FCP∽△PCE,
∴ ,FP=EP,
∴BF=BP+EP,
由“两点之间,线段最短”可得:BF的长即BP+EP为最小值.
∵CF=CE,E(2,8),
∴F(,),
∴BF=
【点睛】
本题考查二次函数综合,待定系数法,二次函数图象和性质,勾股定理及其逆定理,圆的性质,相似三角形的判定和性质等,题目综合性较强,属于中考压轴题,熟练掌握二次函数图象和性质,圆的性质,相似三角形的判定和性质等相关知识是解题关键.
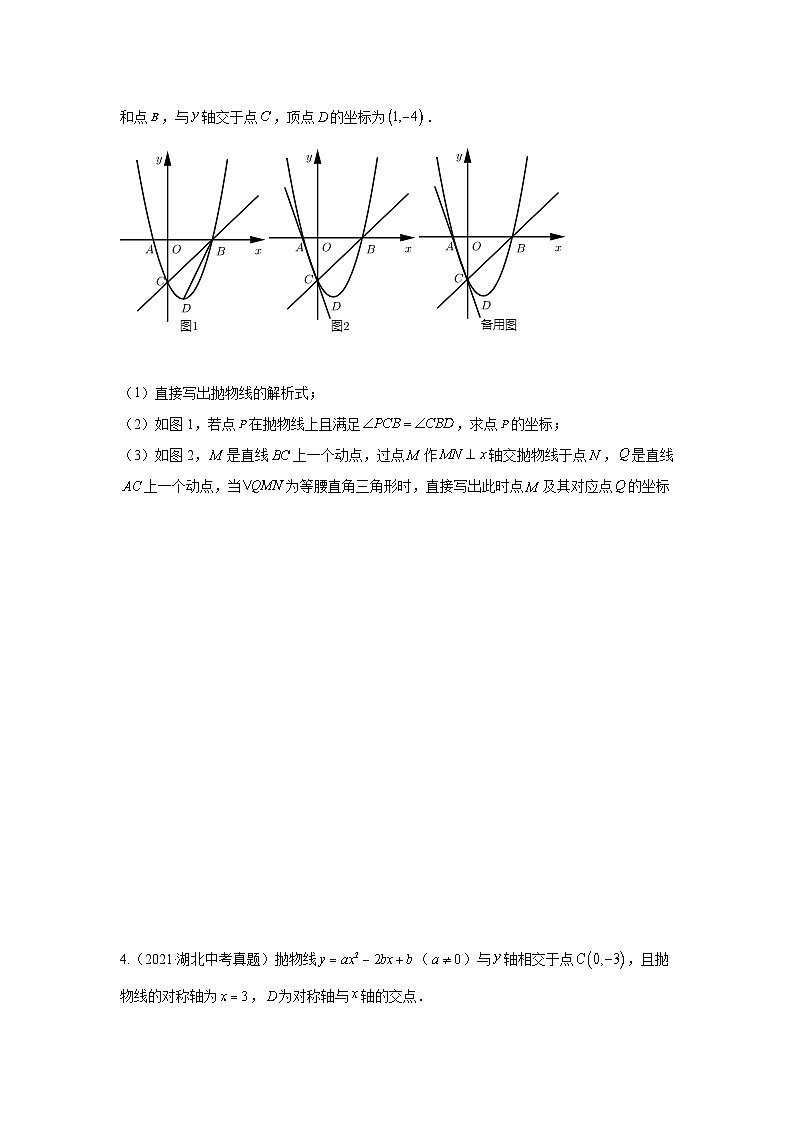
3.(2021·湖北中考真题)在平面直角坐标系中,抛物线与轴交于点和点,与轴交于点,顶点的坐标为.
(1)直接写出抛物线的解析式;
(2)如图1,若点在抛物线上且满足,求点的坐标;
(3)如图2,是直线上一个动点,过点作轴交抛物线于点,是直线上一个动点,当为等腰直角三角形时,直接写出此时点及其对应点的坐标
【答案】(1);(2),;(3),;,;,;,; ,;,.
【分析】
(1)由和,且D为顶点列方程求出a、b、c,即可求得解析式;
(2)分两种情况讨论:①过点作,交抛物线于点,②在下方作交于点,交抛物线于;
(3)为等腰直角三角形,分三种情况讨论:当;②当;③当.
【详解】
解:(1)将和代入
得
又∵顶点的坐标为
∴
∴解得
∴抛物线的解析式为:.
(2)∵和
∴直线的解析式为:
∵抛物线的解析式为:,抛物线与轴交于点,与轴交于点和点,
则C点坐标为,B点坐标为.
①过点作,交抛物线于点,
则直线的解析式为,
结合抛物线可知,
解得:(舍),,
故.
②过点作轴平行线,过点作轴平行线交于点,
由可知四边形为正方形,
∵直线的解析式为
∴与轴交于点,
在下方作交于点,交抛物线于
∴
又∵OC=CG,
∴≌,
∴,,
又由可得
直线的解析式为,
结合抛物线可知,
解得(舍),,
故.
综上所述,符合条件的点坐标为:,.
(3)∵,
∴直线的解析式为
设M的坐标为,则N的坐标为
∴
∵,
∴直线的解析式为
∵为等腰直角三角形
∴①当时,如下图所示
则Q点的坐标为
∴
∴
解得:(舍去),,
∴此时,;,;
②当时,如下图所示
则Q点的坐标为
∴
∴
解得:(舍去),,
∴此时,;,;
③当时,如图所示
则Q点纵坐标为
∴Q点的坐标为
∴Q点到MN的距离=
∴(直角三角形斜边上的中线等于斜边的一半)
解得:(舍去),,
∴此时,;,.
综上所述,点及其对应点的坐标为:,;,;,;,; ,;,.
【点睛】
本题主要考查二次函数与几何图形.该题综合性较强,属于中考压轴题.
4.(2021·湖北中考真题)抛物线()与轴相交于点,且抛物线的对称轴为,为对称轴与轴的交点.
(1)求抛物线的解析式;
(2)在轴上方且平行于轴的直线与抛物线从左到右依次交于、两点,若是等腰直角三角形,求的面积;
(3)若是对称轴上一定点,是抛物线上的动点,求的最小值(用含的代数式表示).
【答案】(1);(2)4;(3)
【分析】
(1)与轴相交于点,得到,再根据抛物线对称轴,求得,代入即可.
(2)在轴上方且平行于轴的直线与抛物线从左到右依次交于、两点,可知、两点关于对称轴对称,是等腰直角三角形得到,设,根据等腰直角三角形的性质求得E点坐标,从而求得的面积.
(3),根据距离公式求得,注意到的范围,利用二次函数的性质,对进行分类讨论,从而求得的最小值.
【详解】
解:(1)由抛物线()与轴相交于点得到
抛物线的对称轴为,即,解得
∴抛物线的方程为
(2)过点E作交AB于点M,过点F作,交AB于点N,如下图:
∵是等腰直角三角形
∴,
又∵轴
∴
∴为等腰直角三角形
∴
设,则,
∴
又∵
∴
解得或
当时,,符合题意,
当时,,不符合题意
综上所述:.
(3)设,在抛物线上,则
将代入上式,得
当时,,∴时,最小,即最小
=
当时,,∴时,最小,即最小
,
综上所述
【点睛】
此题考查了二次函数的对称轴、二次函数与三角形面积、等腰直角三角形的性质以及距离公式等知识,熟练掌握距离公式和对代数式的计算是解决本题的关键.
5.(2020•泸州)如图,已知抛物线y=ax2+bx+c经过A(﹣2,0),B(4,0),C(0,4)三点.
(1)求该抛物线的解析式;
(2)经过点B的直线交y轴于点D,交线段AC于点E,若BD=5DE.
①求直线BD的解析式;
②已知点Q在该抛物线的对称轴l上,且纵坐标为1,点P是该抛物线上位于第一象限的动点,且在l右侧,点R是直线BD上的动点,若△PQR是以点Q为直角顶点的等腰直角三角形,求点P的坐标.
【分析】
(1)根据交点式设出抛物线的解析式,再将点C坐标代入抛物线交点式中,即可求出a,即可得出结论;
(2)①先利用待定系数法求出直线AC的解析式,再利用相似三角形得出比例式求出BF,进而得出点E坐标,最后用待定系数法,即可得出结论;
②先确定出点Q的坐标,设点P(x,x2+x+4)(1<x<4),得出PG=x﹣1,GQx2+x+3,再利用三垂线构造出△PQG≌△QRH(AAS),得出RH=GQx2+x+3,QH=PG=x﹣1,进而得出R(x2+x+4,2﹣x),最后代入直线BD的解析式中,即可求出x的值,即可得出结论.
【解析】
(1)∵抛物线y=ax2+bx+c经过A(﹣2,0),B(4,0),
∴设抛物线的解析式为y=a(x+2)(x﹣4),
将点C坐标(0,4)代入抛物线的解析式为y=a(x+2)(x﹣4)中,得﹣8a=4,
∴a,
∴抛物线的解析式为y(x+2)(x﹣4)x2+x+4;
(2)①如图1,
设直线AC的解析式为y=kx+b',
将点A(﹣2,0),C(0,4),代入y=kx+b'中,得,
∴,
∴直线AC的解析式为y=2x+4,
过点E作EF⊥x轴于F,
∴OD∥EF,
∴△BOD∽△BFE,
∴,
∵B(4,0),
∴OB=4,
∵BD=5DE,
∴,
∴BFOB4,
∴OF=BF﹣OB4,
将x代入直线AC:y=2x+4中,得y=2×()+4,
∴E(,),
设直线BD的解析式为y=mx+n,
∴,
∴,
∴直线BD的解析式为yx+2;
②∵抛物线与x轴的交点坐标为A(﹣2,0)和B(4,0),
∴抛物线的对称轴为直线x=1,
∴点Q(1,1),如图2,
设点P(x,x2+x+4)(1<x<4),
过点P作PG⊥l于G,过点R作RH⊥l于H,
∴PG=x﹣1,GQx2+x+4﹣1x2+x+3,
∵PG⊥l,∴∠PGQ=90°,
∴∠GPQ+∠PQG=90°,
∵△PQR是以点Q为直角顶点的等腰直角三角形,
∴PQ=RQ,∠PQR=90°,
∴∠PQG+∠RQH=90°,
∴∠GPQ=∠HQR,
∴△PQG≌△QRH(AAS),
∴RH=GQx2+x+3,QH=PG=x﹣1,
∴R(x2+x+4,2﹣x),
由①知,直线BD的解析式为yx+2,
∴x=2或x=4(舍),
当x=2时,yx2+x+44+2+4=4,
∴P(2,4).
6.(2020·甘肃兰州?中考真题)如图,抛物线经过A(-3,6),B(5,-4)两点,与y轴交于点C,连接AB,AC,BC.
(1)求抛物线的表达式;
(2)求证:AB平分;
(3)抛物线的对称轴上是否存在点M,使得是以AB为直角边的直角三角形.若存在,求出点M的坐标;若不存在,说明理由.
【答案】(1);(2)详见解析;(3)存在,点M的坐标为(,-9)或(,11).
【解析】
【分析】
(1)将A(-3,0),B(5,-4)代入抛物线的解析式得到关于a、b的方程组,从而可求得a、b的值;
(2)先求得AC的长,然后取D(2,0),则AD=AC,连接BD,接下来,证明BC=BD,然后依据SSS可证明△ABC≌△ABD,接下来,依据全等三角形的性质可得到∠CAB=∠BAD;
(3)作抛物线的对称轴交x轴与点E,交BC与点F,作点A作AM′⊥AB,作BM⊥AB,分别交抛物线的对称轴与M′、M,依据点A和点B的坐标可得到tan∠BAE=,从而可得到tan∠M′AE=2或tan∠MBF=2,从而可得到FM和M′E的长,故此可得到点M′和点M的坐标.
【详解】
解:(1)将A(-3,0),B(5,-4)两点的坐标分别代入,
得
解得
故抛物线的表达式为y=.
(2)证明:∵AO=3,OC=4,
∴AC==5.
取D(2,0),则AD=AC=5.
由两点间的距离公式可知BD==5.
∵C(0,-4),B(5,-4),
∴BC=5.
∴BD=BC.
在△ABC和△ABD中,AD=AC,AB=AB,BD=BC,
∴△ABC≌△ABD,
∴∠CAB=∠BAD,
∴AB平分∠CAO;
(3)存在.如图所示:抛物线的对称轴交x轴与点E,交BC与点F.
抛物线的对称轴为x=,则AE=.
∵A(-3,0),B(5,-4),
∴tan∠EAB=.
∵∠M′AB=90°.
∴tan∠M′AE=2.
∴M′E=2AE=11,
∴M′(,11).
同理:tan∠MBF=2.
又∵BF=,
∴FM=5,
∴M(,-9).
∴点M的坐标为(,11)或(,-9).
【点睛】
本题考查了二次函数的综合应用,主要应用了待定系数法求二次函数的解析式,全等三角形的性质和判定、锐角三角函数的定义,求得FM和M′E的长是解题的关键
7.(2020·内蒙古通辽?中考真题)如图,在平面直角坐标系中,抛物线与x轴交于点,与y轴交于点C,且直线过点B,与y轴交于点D,点C与点D关于x轴对称.点P是线段上一动点,过点P作x轴的垂线交抛物线于点M,交直线于点N.
(1)求抛物线的函数解析式;
(2)当的面积最大时,求点P的坐标;
(3)在(2)的条件下,在y轴上是否存在点Q,使得以三点为顶点的三角形是直角三角形,若存在,直接写出点Q的坐标;若不存在,说明理由.
【答案】(1);(2)(2,0);(3)存在,(0,12)或(0,-4)或(0,)或(0,).
【解析】
【分析】
(1)根据直线求出点B和点D坐标,再根据C和D之间的关系求出点C坐标,最后运用待定系数法求出抛物线表达式;
(2)设点P坐标为(m,0),表示出M和N的坐标,再利用三角形面积求法得出S△BMD=,再求最值即可;
(3)分当∠QMN=90°时,当∠QNM=90°时,当∠MQN=90°时,三种情况,结合相似三角形的判定和性质,分别求解即可.
【详解】
解:(1)∵直线过点B,点B在x轴上,
令y=0,解得x=6,令x=0,解得y=-6,
∴B(6,0),D(0,-6),
∵点C和点D关于x轴对称,
∴C(0,6),
∵抛物线经过点B和点C,代入,
,解得:,
∴抛物线的表达式为:;
(2)设点P坐标为(m,0),
则点M坐标为(m,),点N坐标为(m,m-6),
∴MN=-m+6=,
∴S△BMD=S△MNB+S△MND
=
=
=-3(m-2)2+48
当m=2时,S△BMD最大=48,
此时点P的坐标为(2,0);
(3)存在,
由(2)可得:M(2,12),N(2,-4),
设点Q的坐标为(0,n),
当∠QMN=90°时,即QM⊥MN,如图,
可得,此时点Q和点M的纵坐标相等,
即Q(0,12);
当∠QNM=90°时,即QN⊥MN,如图,
可得,此时点Q和点N的纵坐标相等,
即Q(0,-4);
当∠MQN=90°时,MQ⊥NQ,如图,
分别过点M和N作y轴的垂线,垂足为E和F,
∵∠MQN=90°,
∴∠MQE+∠NQF=90°,又∠MQE+∠QME=90°,
∴∠NQF=∠QME,
∴△MEQ∽△QFN,
∴,即,
解得:n=或,
∴点Q(0,)或(0,),
综上:点Q的坐标为(0,12)或(0,-4)或(0,)或(0,).
【点睛】
本题是二次函数综合题,考查了二次函数的表达式,相似三角形的判定和性质,直角三角形的性质,二次函数的最值,解一元二次方程,解题时要注意数形结合,分类讨论思想的运用.
中考数学二轮复习重难点复习题型09 二次函数综合题 类型九 二次函数与菱形有关的问题(专题训练)(2份打包,原卷版+解析版): 这是一份中考数学二轮复习重难点复习题型09 二次函数综合题 类型九 二次函数与菱形有关的问题(专题训练)(2份打包,原卷版+解析版),文件包含中考数学二轮复习重难点复习题型09二次函数综合题类型九二次函数与菱形有关的问题专题训练解析版doc、中考数学二轮复习重难点复习题型09二次函数综合题类型九二次函数与菱形有关的问题专题训练原卷版doc等2份试卷配套教学资源,其中试卷共29页, 欢迎下载使用。
中考数学二轮复习重难点复习题型09 二次函数综合题 类型八 二次函数与平行四边形有关的问题(专题训练)(2份打包,原卷版+解析版): 这是一份中考数学二轮复习重难点复习题型09 二次函数综合题 类型八 二次函数与平行四边形有关的问题(专题训练)(2份打包,原卷版+解析版),文件包含中考数学二轮复习重难点复习题型09二次函数综合题类型八二次函数与平行四边形有关的问题专题训练解析版doc、中考数学二轮复习重难点复习题型09二次函数综合题类型八二次函数与平行四边形有关的问题专题训练原卷版doc等2份试卷配套教学资源,其中试卷共90页, 欢迎下载使用。
中考数学二轮复习重难点复习题型09 二次函数综合题 类型五 二次函数与三角形全等、相似(位似)有关的问题(专题训练)(2份打包,原卷版+解析版): 这是一份中考数学二轮复习重难点复习题型09 二次函数综合题 类型五 二次函数与三角形全等、相似(位似)有关的问题(专题训练)(2份打包,原卷版+解析版),文件包含中考数学二轮复习重难点复习题型09二次函数综合题类型五二次函数与三角形全等相似位似有关的问题专题训练解析版doc、中考数学二轮复习重难点复习题型09二次函数综合题类型五二次函数与三角形全等相似位似有关的问题专题训练原卷版doc等2份试卷配套教学资源,其中试卷共44页, 欢迎下载使用。












