高中数学人教A版 (2019)必修 第一册3.2 函数的基本性质图片ppt课件

这是一份高中数学人教A版 (2019)必修 第一册3.2 函数的基本性质图片ppt课件，共25页。PPT课件主要包含了f-3f3，f-2f2，f-1f1，g-3g3，g-2g2，g-1g1，定义域关于原点对称，1fxx4，2fxx5，方法总结等内容，欢迎下载使用。

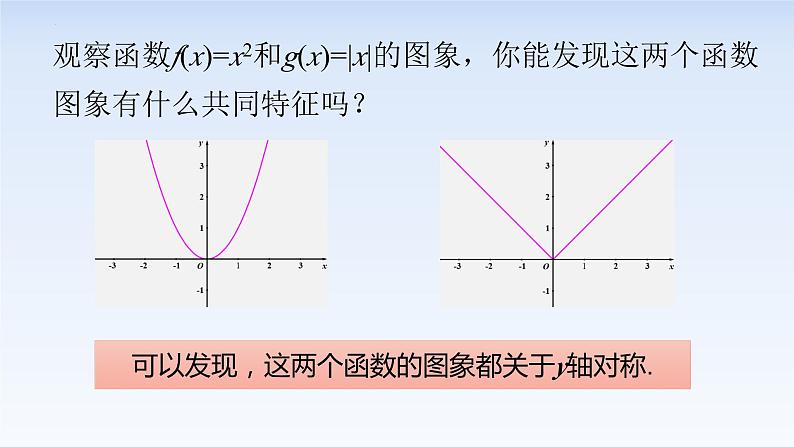
观察函数f(x)=x2和g(x)=|x|的图象，你能发现这两个函数图象有什么共同特征吗？
可以发现，这两个函数的图象都关于y轴对称.
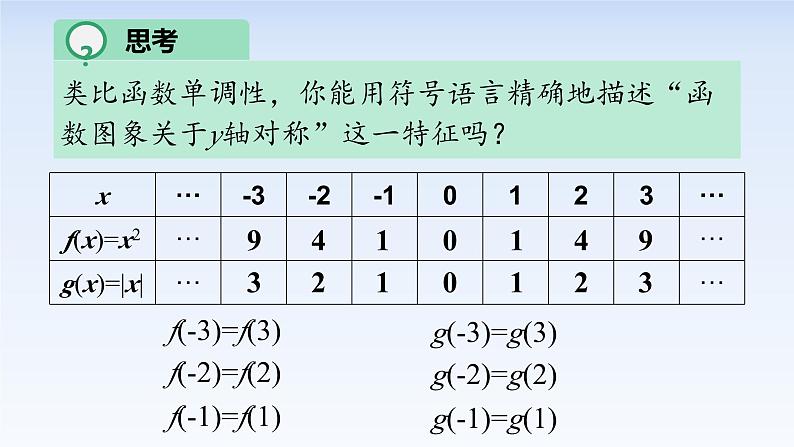
类比函数单调性，你能用符号语言精确地描述“函数图象关于y轴对称”这一特征吗？
PART 1 偶函数
定义：设函数f(x)的定义域为I，如果∀x∈I，都有-x∈I， 且f(-x)＝f(x)，那么函数f(x)就叫做偶函数.
变形：f(-x)-f(x)＝0
图象特征：关于y轴对称.
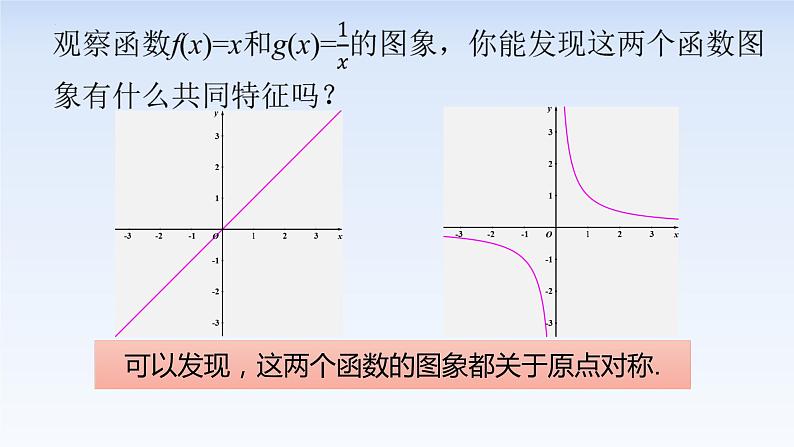
可以发现，这两个函数的图象都关于原点对称.
可以发现，两个函数的图象都关于原点成中心对称图形，为了用符号语言描述这一特征，不妨取自变量的一些特殊值，看相应函数值的情况.
f(-3)=-f(3)
f(-2)=-f(2)
f(-1)=-f(1)
g(-3)=-g(3)
g(-2)=-g(2)
g(-1)=-g(1)
PART 2 奇函数
定义：设函数f(x)的定义域为I，如果∀x∈I，都有-x∈I， 且f(-x)＝-f(x)，那么函数f(x)就叫做奇函数.
变形：f(-x)+f(x)＝0
图象特征：关于原点对称.
若函数f(x)是定义域为R的奇函数，则f(0)的值是多少？
因为函数f(x)是奇函数，所以f(-x)=-f(x)，即f(-x)+f(x)=0，当x=0时，f(0)+f(0)=0,即f(0)=0.
f(x)为奇函数且x=0处有定义，则f(0)=0
根据奇偶性，函数分为四类： 1.奇函数 2.偶函数 3.既奇又偶 （f(x)=0，定义域关于原点对称） 4.非奇非偶
例 判断下列函数的奇偶性：
解：(1)函数f(x)定义域为R，∀x∈R ，都有-x∈R， 且f(-x)=(-x)4=x4=f(x)， 所以函数f(x)是偶函数.
（2）函数f(x)定义域为{x|x≠0}， ∀x∈{x|x≠0}，都有-x∈{x|x≠0}， 且 ， 所以函数f(x)是奇函数.
（3）函数f(x)定义域为{x|x≥0}， ∃x0∈{x|x≥0}，-x ∉{x|x≥0}， 所以函数f(x)是既不是奇函数也不是偶函数.
（4）函数f(x)定义域为R，∀x∈R，都有-x∈R， 且f(-x)=0=f(x)=-f(x)， 所以函数f(x)既是奇函数也是偶函数.
判断函数奇偶性的方法：
①判断定义域是否关于原点对称；
②计算f(-x)与f(x)的关系；
①判断函数图象是否关于y轴或原点对称；
题型一 函数的奇偶性的判断
例1 判断下列函数的奇偶性
解:(1)函数 f(x)=x3 的定义域是R，且 f(-x)=-x3=-f(x)，所以函数 f(x)=x3 是奇函数.
(2)函数 f(x)=|x+1|-|x-1| 的定义域是R，且 f(-x)=|-x+1|-|-x-1|=-f(x)，所以函数 f(x)=|x+1|-|x-1| 是奇函数.
巩固练习 1 判断下列函数的奇偶性
解:(1)函数 f(x)=1 的定义域是R，且 f(-x)=f(x)，所以函数 f(x)=1 是偶函数.
(2)函数 f(x)=-x2+1 的定义域是R，且 f(-x)=-x2+1=f(x)，所以函数 f(x)=-x2+1 是偶函数.
巩固练习 2 若函数y＝f(x)，x∈[－2，a]是偶函数，则a的值为(　　)A．－2 B．2C．0 D．不能确定
题型二 奇偶函数的图象
例2 已知函数f(x)是偶函数，g(x)是奇函数，试将下图补充完整.
巩固练习 1 设奇函数f(x)的定义域为[－5,5]，若当x∈[0,5]时，f(x)的图象如图，则不等式f(x)<0的解集是______．
解析：由奇函数的性质知，其图象关于原点对称，则f(x)在定义域[－5,5]上的图象如图，由图可知不等式f(x)<0的解集为{x|－2巩固练习 2 如图，给出了偶函数y＝f(x)的局部图象，试比较f(1)与f(3)的大小．
解析：因函数f(x)是偶函数， 所以其图象关于y轴对称， 补全图如图．
由图象可知f(1)题型三 抽象函数奇偶性的判断
例3 若函数f(x)的定义域是R，且对任意x,y∈R，都有f(x+y)=f(x)+f(y)成立，试判断f(x)的奇偶性.
解：令x=y=0得f(0+0)=f(0)+f(0),即f(0)=0.∴f(0)=f(x-x)=f(x)+f(-x)=0∴f(-x)=-f(x) ∴f(x)为奇函数.