2023年山东省青岛市市南区中考三模数学试题
展开
这是一份2023年山东省青岛市市南区中考三模数学试题,共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年山东省青岛市市南区中考数学三模试卷
一、选择题(本大题共8小题,共24.0分。在每小题列出的选项中,选出符合题目的一项)
1.下列各组数中互为相反数的是( )
A.5和 B.和-(-5) C.-5和 D.-5和
2.某网店2023年母亲节这天的营业额为2210000元,将数2210000用科学记数法表示为( )
A. B. C. D.
3.下列四个银行标志中,既是中心对称图形,又是轴对称图形的是( )
A. B. C. D.
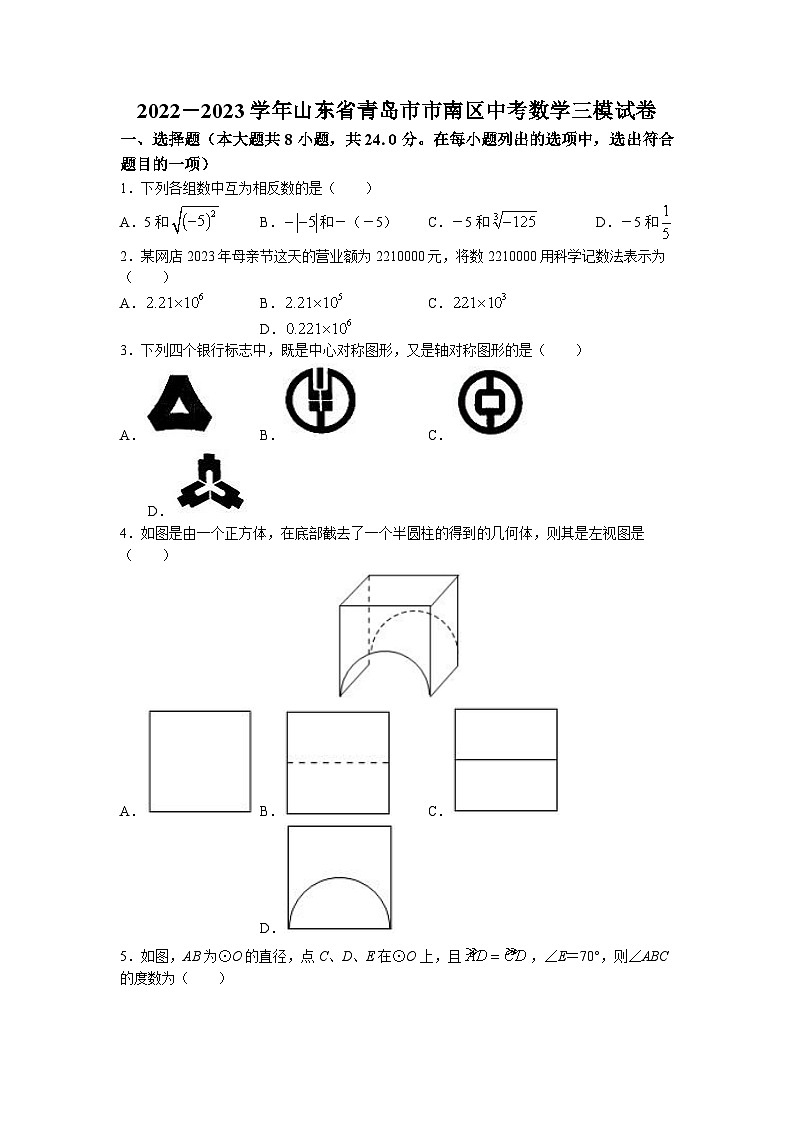
4.如图是由一个正方体,在底部截去了一个半圆柱的得到的几何体,则其是左视图是( )
A. B. C. D.
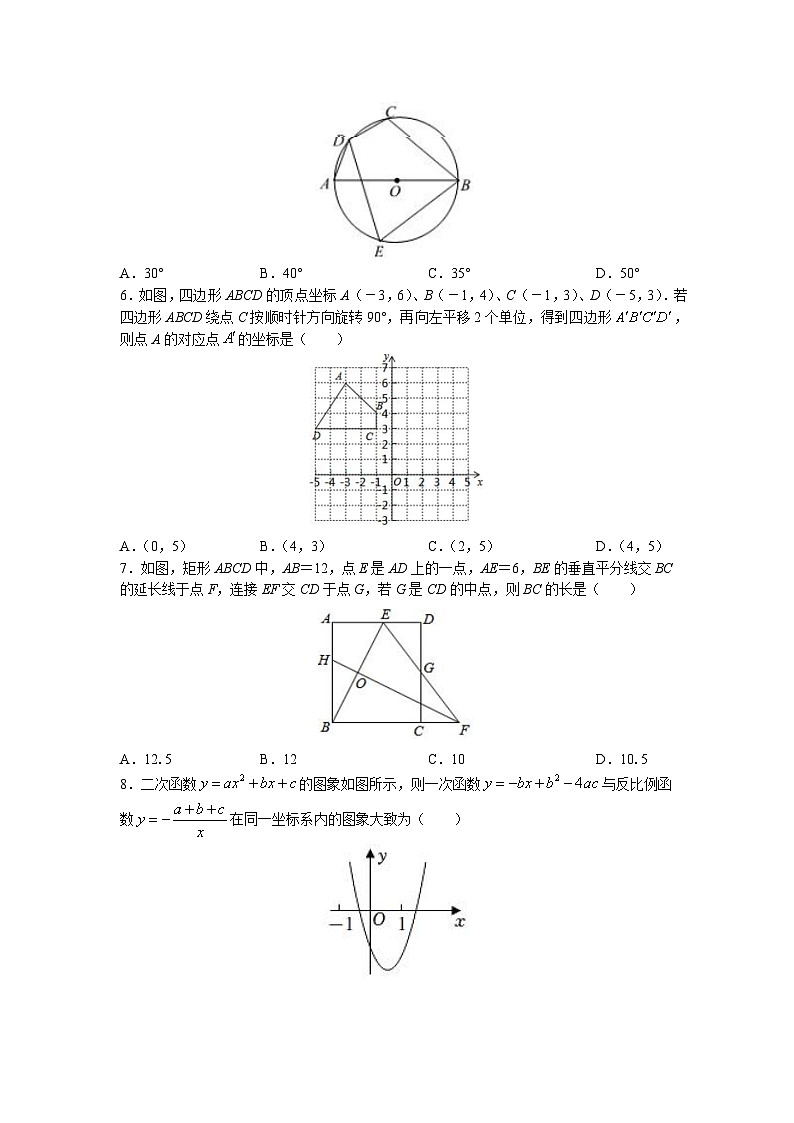
5.如图,AB为⊙O的直径,点C、D、E在⊙O上,且,∠E=70°,则∠ABC的度数为( )
A.30° B.40° C.35° D.50°
6.如图,四边形ABCD的顶点坐标A(-3,6)、B(-1,4)、C(-1,3)、D(-5,3).若四边形ABCD绕点C按顺时针方向旋转90°,再向左平移2个单位,得到四边形,则点A的对应点的坐标是( )
A.(0,5) B.(4,3) C.(2,5) D.(4,5)
7.如图,矩形ABCD中,AB=12,点E是AD上的一点,AE=6,BE的垂直平分线交BC的延长线于点F,连接EF交CD于点G,若G是CD的中点,则BC的长是( )
A.12.5 B.12 C.10 D.10.5
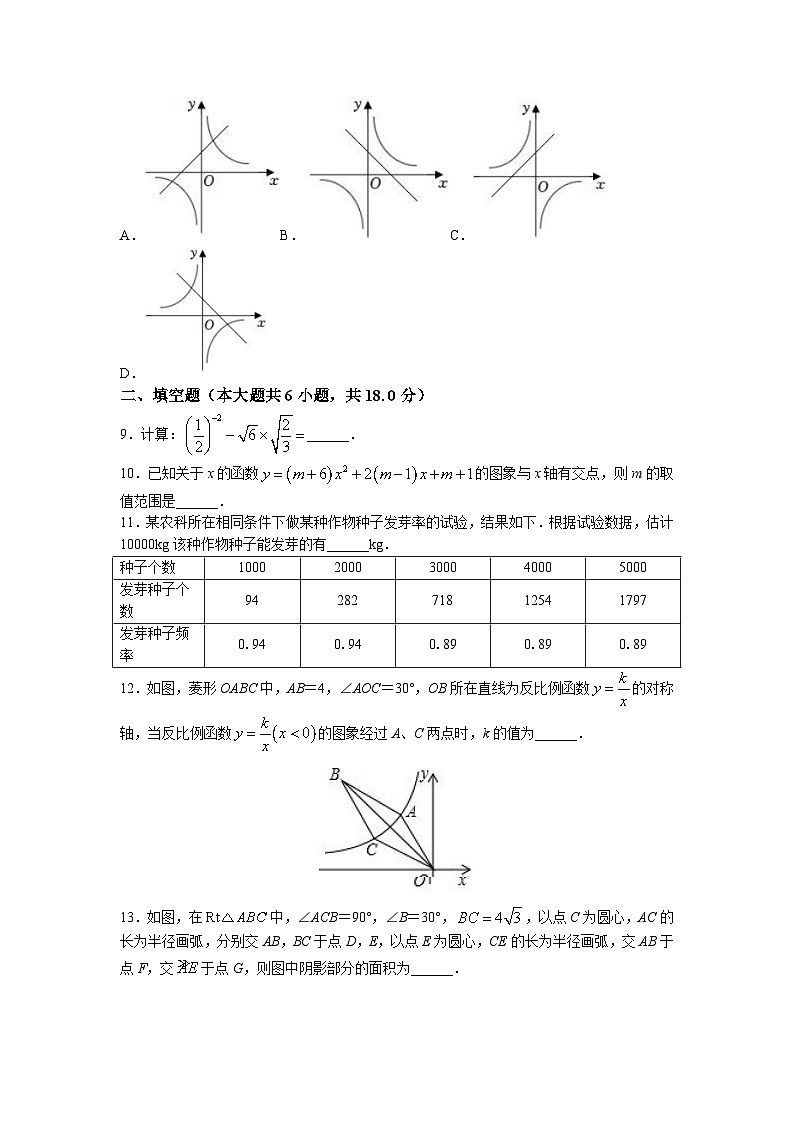
8.二次函数的图象如图所示,则一次函数与反比例函数在同一坐标系内的图象大致为( )
A.B.C.D.
二、填空题(本大题共6小题,共18.0分)
9.计算:______.
10.已知关于x的函数的图象与x轴有交点,则m的取值范围是______.
11.某农科所在相同条件下做某种作物种子发芽率的试验,结果如下.根据试验数据,估计10000kg该种作物种子能发芽的有______kg.
种子个数
1000
2000
3000
4000
5000
发芽种子个数
94
282
718
1254
1797
发芽种子频率
0.94
0.94
0.89
0.89
0.89
12.如图,菱形OABC中,AB=4,∠AOC=30°,OB所在直线为反比例函数的对称轴,当反比例函数的图象经过A、C两点时,k的值为______.
13.如图,在中,∠ACB=90°,∠B=30°,,以点C为圆心,AC的长为半径画弧,分别交AB,BC于点D,E,以点E为圆心,CE的长为半径画弧,交AB于点F,交于点G,则图中阴影部分的面积为______.
14.如图,在矩形ABCD中,AB=3,AD=9,点E,F分别在边AD,BC上,且AE=2,沿直线EF翻折,点A的对应点恰好落在对角线AC上,点B的对应点为,分别在线段EF,上取点M,N,沿直线MN二次翻折,使点F与点E重合,则线段MN的长为______.
三、解答题(本大题共11小题,共78.0分。解答应写出文字说明,证明过程或演算步骤)
15.(本小题4.0分)
已知:∠AOB内一点C及线段a,求作:∠AOB内的点P,使P点到射线OA,OB的距离相等且PC=a.
16.(本小题8.0分)
(1)化简:;
(2)解不等式组:.
17.(本小题6.0分)
某商场,为了吸引顾客,在“元旦”当天举办了商品有奖酬宾活动,凡购物满200元者,有两种奖励方案供选择:
方案一:是直接获得20元的礼金券;
方案二:是得到一次摇奖的机会.规则如下:已知如图是由转盘和箭头组成的两个转盘A、B,这两个转盘除了颜色不同外,其它构造完全相同,摇奖者同时转动两个转盘,指针分别指向一个区域(指针落在分割线上时重新转动转盘),根据指针指向的区域颜色(如表)决定送礼金券的多少.
指针指向
两红
一红一蓝
两蓝
礼金券(元)
18
9
18
A款 B款
(1)请你用列表法(或画树状图法)求两款转盘指针分别指向一红区和一蓝区的概率.
(2)如果一名顾客当天在本店购物满200元,若只考虑获得最多的礼品券,请你帮助分析选择哪种方案较为实惠.
18.(本小题6.0分)
《中学生体质健康标准》规定学生体质健康等级标准:90分及以上为优秀;80分~89分为良好;60分~79分为及格;60分以下为不及格,某校为了解学生的体质健康情况,从年级学生中随机抽取了10%的学生进行了体质测试,并将测试数据制成如下统计图.
各等级学生平均分 各等级人数百分比
(1)扇形统计图中,“优秀”等级所在扇形圆心角的度数是______°;
(2)求参加本次测试学生的平均成绩;
(3)若参加本次测试“良好”及“良好”以上等级的学生共有35人,请你估计全校年级“不及格”等级的学生大约有多少人.
19.(本小题6.0分)
如图所示,小明和小华约定一同去中山公园游玩,公园有东西两个门,西门A在东门B的正西方向,小明自公园西门A处出发,沿北偏东53°方向前往游乐场D处;小华自东门B处出发,沿正北方向行走150来到达C处,再沿西偏北22.6°方向前往游乐场D处与小明汇合,若两人所走的路程相同,求公园西门A与游乐场D之间的距离.
(结果保留整数,参考数据:,,,,,)
20.(本小题6.0分)
如图,在⊙O中,点E是直径AB与弦CD的交点,点F为直径AB延长线上一点,且FC=AC,若.
(1)求证:CF是⊙O的切线;
(2)若AE=4,OE=1,求DE的长.
21.(本小题6.0分)
【问题提出】已知任意三角形的两边及夹角,求三角形的面积.
【性质探究】
探究一:如图1,在中,∠ABC=90°,AC=b,BC=a,∠C=∠α,
∵∠ABC=90°,∴
∴,∴
探究二:如图2,中,AB=AC=b,BC=a,∠B=∠α,求的面积(用含a、b、α代数式表示),写出探究过程.
探究三:中,AB=b,BC=a,∠B=∠α,求的面积(用a、b、α表示)写出探究过程.
【性质应用】
(1)如图4,已知平行四边形ABCD中.AB=b,BC=a,∠B=α,求平行四边形ABCD的面积(用a、b、α表示)写出解题过程.
(2)如图5所示,利用你所探究的结论直接写出任意四边形的面积(用a、b、c、d、a、β表示),其中AB=b,BC=c,CD=d,AD=a,∠A=α,∠C=β.
22.(本小题8.0分)
如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第一、三象限内的A,B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,-2),.
(1)求反比例函数和一次函数的表达式;
(2)将直线AB沿y轴向下平移6个单位长度后,与双曲线交于E,F两点,连接OE,OF,求的面积.
23.(本小题8.0分)
如图,在矩形ABCD中,点G,H是对角线AC上的两点,且AG=CH,过AC的中点O作交AB于点E,交CD于点F.
(1)求证:;
(2)若∠BAC+∠CFH=45°,请你判断四边形GEHF的形状,并说明理由.
24.(本小题10.0分)
“净扬”水净化有限公司用160万元,作为新产品的研发费用,成功研制出了一种市场急需的小型水净化产品,已于当年投入生产并进行销售.已知生产这种小型水净化产品的成本为4元/件,在销售过程中发现:每年的年销售量y(万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,BC为一次函数图象的一部分.设公司销售这种水净化产品的年利润为z(万元)(注:若上一年盈利,则盈利不计入下一年的年利润;若上一年亏损,则亏损计作下一年的成本.)
(1)请求出y(万件)与x(元/件)之间的函数关系式;
(2)求出第一年这种水净化产品的年利润z(万元)与x(元/件)之间的函数关系式,并求出第一年年利润的最大值;
(3)假设公司的这种水净化产品第一年恰好按年利润z(万元)取得最大值时进行销售,现根据第一年的盈亏情况,决定第二年将这种水净化产品每件的销售价格x(元)定在8元以上(x>8),当第二年的年利润不低于103万元时,请结合年利润z(万元)与销售价格x(元/件)的函数示意图,求销售价格x(元/件)的取值范围.
25.(本小题10.0分)
已知:如图1,在ABCD中,AB=10cm,AD=8cm,对角线AC的长为6cm,将沿射线CB方向以2cm/s的速度运动,经平移得到AEBF(如图2);同时,点P从点E以2cm/s的速度向点B运动,点Q从点C以1cm/s的速度向点D运动.过点P作交BC于点G,连接PQ,交EF于点O,设运动时间为.解答下列问题:
(1)当PQ平分∠EPG时,求t的值;
(2)连接AP、AQ,设的面积为S(cm²).求S与t的函数关系式;
(3)是否存在某一时刻,使B、O、D三点共线?若存在,请求出t值,并求出此时点G到PQ的距离;若不存在,请说明理由.
答案和解析
1.【答案】B【解析】解:A、,相等,故选项错误;
B、,-(-5)=5,互为相反数,故选项正确;
C、,相等,故选项错误;D、-5和不是相反数,故想错误.
故选:B.
由于只是符号不同的两个数叫做互为相反数,它们的和为0,由此即可判定选择项.
本题考查了互为相反数的意义,只是符号不同的两个数叫做互为相反数.
2.【答案】A【解析】解:.
故选:A.
科学记数法的表示形式为的形式,其中,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同,当原数绝对值≥10时,n是正整数;当原数的绝对值0.
对称轴在y轴的右侧,则a、b异号,所以b0.又因为抛物线与x轴有2个交点,
所以,所以直线经过第一、二、三象限.
当x=1时,y4,
所以选择方案一,即直接获得20元的礼金券比较实惠.
【解析】(1)用列表法列举所有可能出现的结果,即可求出两款转盘指针分别指向一红区和一蓝区的概率;
(2)分别求出一红一蓝,两红、两蓝的概率,进而求出平均每次所获的奖券的金额即可.
本题考查列表法或树状图法求简单随机事件的概率,列举出所有可能出现的结果是正确解答的关键.
18.【答案】72【解析】解:(1)“优秀”等级所在扇形圆心角的度数是;故答案为:72.
(2)参加本次测试学生的平均成绩是:
(分);
(3)根据题意得:(人),
答:全校八年级“不及格”等级的学生大约有25人.
(1)用360°乘以“优秀”所占的百分比即可得出答案;
(2)利用加权平均数公式计算即可;
(3)根据“良好”及“良好”以上等级的学生数和所占的百分比求出抽取的人数,再求出全校的总人数,然后乘以“不及格”等级的学生所占的百分比即可得出答案.
本题考查条形统计图,扇形统计图,加权平均数等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
19.【答案】解:过点D作DE⊥AB,垂足为E,过点C作CF⊥DE,垂足为F,
由题意得:BC=EF=150米,设CD=x米,在中,∠DCF=22.6°,
∴(米),∴米,
在中,∠DAE=90°-53°=37°,∴米,
∵AD=DC+BC,∴,解得:,
∴(米),∴公园西门A与游乐场D之间的距离约为429米.
【解析】过点D作DE⊥AB,垂足为E,过点C作CF⊥DE,垂足为F,根据题意可得:BC=EF=150米,然后设CD=x米,在中,利用锐角三角函数的定义求出DF的长,从而求出DE的长,再在中,利用锐角三角函数的定义求出AD的长,最后根据AD=DC+BC,列出关于x的方程,进行计算即可解答.
本题考查了解直角三角形的应用—方向角问题,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
20.【答案】(1)证明:连接CO,如图1所示,
∵FC=AC,∴∠A=∠F,
∵∠A=∠D=30°,∴∠F=30°,∠COB=2∠D=60°,∴∠FCO=90°,∴CO⊥CF,
∵CO为⊙O的半径,∴CF为⊙O的切线;
(2)解:连接BC,过点E作EH⊥BC于点H,如图2所示:
∵AE=4,OE=1,∴AO=OB=OC=3,BE=OB-OE=2,
∵AB为⊙O的直径,∴∠ACB=90°,∵∠A=30°,∴,
在中,,,
∴,在中,,
∵∠D=∠A,∠BED=∠CEA,∴,∴,
即:,解得:,故DE的长为.
【解析】(1)连接CO,如图1所示,根据等腰三角形的性质得到∠A=∠F,根据圆周角定理得到,求得∠FCO=90°,根据切线的判定定理即可得到结论;
(2)连接BC,过点E作EH⊥BC于点H,如图2所示:根据已知条件得到的AO=OB=OC=3,,根据圆周角定理得到∠ACB=90°,根据勾股定理得到,根据相似三角形的性质即可得到结论.
本题考查了切线的判定与性质、圆周角定理、含30°角的直角三角形的性质、相似三角形的判定与性质等知识;熟练掌握切线的判定与性质和相似三角形的判定由V型在是解题的关键.
21.【答案】解:探究二:如图2中,作AH⊥CB于H.
∵AB=AC=b,BC=a,∠B=∠α,∴∠B=∠C=α,
在中,∠AHC=90°,∴,∴,∴;
探究三:如图3中,作AH⊥CB于H.
在中,∠AHC=90°∴,∴
∴;
性质应用(1):如图4中,作AH⊥CB于H.
在中,∠AHB=90°∴,∴
∴;
性质应用(2):
连接BD,由探究三的结论可得:.
.
∴.
【解析】探究二:如图2中,作AH⊥CB于H.求出高AH,即可解决问题;
探究三:如图3中,作AH⊥CB于H.求出高AH,即可解决问题;
性质应用(1):如图4中,作AH⊥CB于H.求出高AH,即可解决问题;
性质应用(2):如图5,连接BD,由探究三的结论可得出答案.
本题考查四边形综合题、三角形的面积、平行四边形的面积、锐角三角函数等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题。
22.【答案】解:(1)过B作BM⊥x轴于M,
∵B(n,-2),.∴BM=2,,∴OM=3,
即B的坐标是(-3,-2),把B的坐标代入得:k=6,即反比例函数的解析式是,
把A(2,m)代入得:m=3,即A的坐标是(2,3),
把A、B的坐标代入得:,解得:,
即一次函数的解析式是;
(2)∵将直线AB沿y轴向下平移6个单位长度后的解析式为,
解,∴或
∴E(6,1),F(-1,-6),
∴的面积.
【解析】(1)解直角三角形求出B的坐标,代入求出反比例函数解析式,求出A的坐标,把A、B的坐标代入一次函数的解析式求出即可;
(2)将直线AB沿y轴向下平移6个单位长度后的解析式为,解方程组得到E(6,1),,于是得到结论.
本题考查了一次函数和反比例函数的交点问题解直角三角形,用待定系数法求一次函数、反比例函数的解析式的应用,主要考查学生的计算能力,题目比较好,难度适中.
23.【答案】(1)证明:∵四边形ABCD是矩形,
∴AO=CO,,∴∠FCH=∠EAG,
在和中,,∴△AOE≌△COF(ASA),∴AE=CF,
在和中,,∴△AEG≌△CFH(SAS);
(2)四边形GEHF是正方形,理由如下:
∵△AEG≌△CFH,∴GE=FH,∠CHF=∠AGE,∴∠FHG=∠EGH,
∴,∴四边形EGFH是平行四边形,
∵EF⊥AC,∴四边形GEHF是菱形,
∵∠OGE=∠BAC+∠AEG=45°,∴∠OEG=45°,∴OE=OG,∴GH=EF,
∴四边形GEHF是正方形.
【解析】(1)由“ASA”可证△AOE≌△COF,可得AE=CF,由“SAS”可证△AEG≌△CFH;
(2)由全等三角形的性质可得GE=FH,∠CHF=∠AGE,可证,可得四边形EGFH是平行四边形,由正方形的判定可证四边形GEHF是正方形.
本题考查了矩形的性质,全等三角形的判定和性质,正方形的判定,证明△AEG≌△CFH是解题的关键.
24.【答案】解:(1)当4≤x≤8时,设,将A(4,40)代入得k=4×40=160,
∴y与x之间的函数关系式为;
当88,∴第二年的年利润,
令s=103,则,
解得,,
在平面直角坐标系中,画出s与x的函数示意图可得:
观察示意图可知,当s≥103时,11≤x≤21,
∴当11≤x≤21时,第二年的年利润s不低于103万元.
【解析】(1)依据待定系数法,即可求出y(万件)与x(元/件)之间的函数关系式;
(2)分两种情况进行讨论,当x=8时,;当x=16时,;根据-16>-80,可得当每件的销售价格定为16元时,第一年年利润的最大值为-16万元;
(3)根据第二年的年利润,令s=103,可得方程,解得,,然后在平面直角坐标系中,画出s与x的函数图象,根据图象即可得出销售价格x(元/件)的取值范围.
本题主要考查了反比例函数与二次函数的综合应用,在商品经营活动中,经常会遇到求最大利润,最大销量等问题,解此类题的关键是通过题意,确定出二次函数的解析式,然后确定其最大值,实际问题中自变量x的取值要使实际问题有意义;解题时注意,依据函数图象可得函数关系式为分段函数,解决问题时需要运用分类思想以及数形结合思想进行求解.
25.【答案】解:(1)如图2,作QX⊥BE于X,作交PG于H,交BE于V,可得四边形BCQV是平行四边形,QH⊥PG,
∵,∴MN⊥BE,
在中,由得,,
在中,,
∴,,
∴,
当PQ平分∠EPG时,QH=QX,∴,
∴t=4,∴满足条件的t的值为4.
(2)如图1中,连接AQ,作AM⊥CD于M,交BE于N,
∵,
,,
∴
;
(3)存在.理由:如图3,连接BD,延长EF交DC的延长线于点T.
在在中,,
∵CQ=t,PE=2t,∴,
∵,∴,∴,
∴t=3,∴满足条件的t的值为3.
【解析】(1)作QX⊥BE于X,作交PG于H,交BE于V,当PQ平分∠EPG时,QH=QX,由此构建方程求解:
(2)如图1中,连接AQ,作AM⊥CD于M,交BE于N,根据,求解即可;
(3)由,推出可得结论.
本题属于几何变换综合题,考查了平行四边形的性质和判定,解直角三角形,平行线分线段成比例定理,角平分线的性质定理等知识,解题的关键是学会利用参数构建方程解决问题,属于中考压轴题.
相关试卷
这是一份2023年山东省青岛市市南区中考三模数学试题,共13页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2023年山东省青岛市市南区中考三模数学试题(含答案),共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2023年山东省青岛市市南区中考二模数学试题,共8页。









