2022-2023学年四川省成都市蓉城高中联盟高二下期期中考试数学（文）试题含解析

2022-2023学年四川省成都市蓉城高中联盟高二下期期中考试数学（文）试题

一、单选题

1．复数的虚部为（    ）

A．1 B． C．2i D．

【答案】D

【分析】依据复数虚部的定义即可求得复数的虚部

【详解】∵的虚部为b，∴的虚部为.

故选：D.

2．某电影院有座位45排，每排有40个座位，在观看《流浪地球2》时恰好坐满了观众.为了了解观众意见，需要抽取45名观众进行座谈，则最合理的抽样方法是（    ）

A．抽签法 B．系统抽样法

C．分层抽样法 D．随机数表法

【答案】B

【分析】根据总体样本的特点可得结果.

【详解】该电影院总体容量较大，又有编号，符合系统抽样的特点，

故最合理的抽样方法为系统抽样，

故选：B.

3．用反证法证明“是无理数”时，正确的假设是（    ）

A．是无理数 B．不是无理数

C．不是有理数 D．是整数

【答案】B

【分析】“反证法”就是从命题的反面即否定形式入手考虑题设.

【详解】“反证法”就是从命题的反面即否定形式推导出否命题是不成立的，

“是无理数”的否定是“不是无理数”.

故选：B.

4．下列导数运算正确的是（    ）

A． B．

C． D．

【答案】C

【分析】根据导数公式判断各项正误即可.

【详解】由，，，，

所以A、B、D错，C对.

故选：C

5．已知函数的导函数的图象如图所示，则函数（    ）

A．在上单调递减 B．在上单调递增

C．在R上单调递减 D．在R上单调递增

【答案】D

【分析】根据导函数的符号确定单调性.

【详解】∵导函数图象在x轴及x轴上方，则，函数为增函数,

∴在R上递增.

故选：D.

6．已知，则曲线在点处的切线方程为（    ）

A． B．

C． D．

【答案】A

【分析】根据导数的几何含义求出切线的斜率及切点，写出切线方程.

【详解】已知，∵，∴，

又，∴切线过，

∴所求切线为，即，

故选：A.

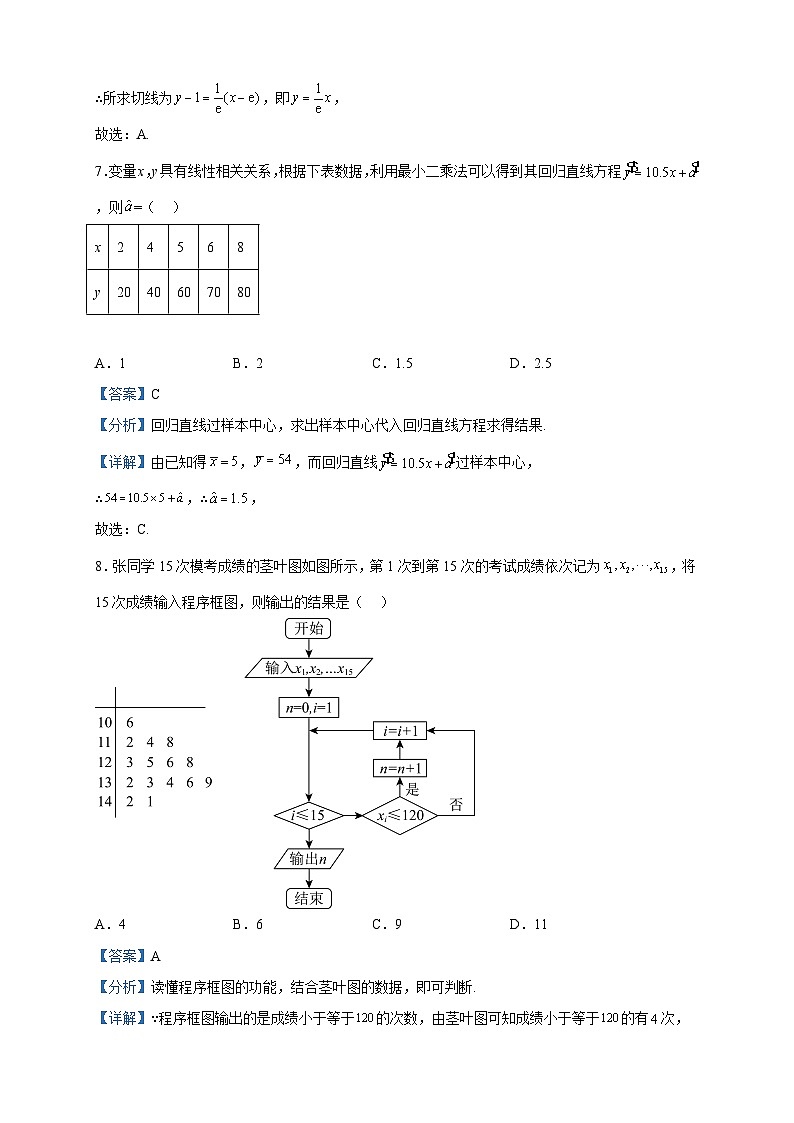
7．变量x，y具有线性相关关系，根据下表数据，利用最小二乘法可以得到其回归直线方程，则=（    ）

A．1 B．2 C．1.5 D．2.5

【答案】C

【分析】回归直线过样本中心，求出样本中心代入回归直线方程求得结果.

【详解】由已知得，，而回归直线过样本中心，

∴，∴，

故选：C.

8．张同学15次模考成绩的茎叶图如图所示，第1次到第15次的考试成绩依次记为，将15次成绩输入程序框图，则输出的结果是（    ）

A．4 B．6 C．9 D．11

【答案】A

【分析】读懂程序框图的功能，结合茎叶图的数据，即可判断.

【详解】∵程序框图输出的是成绩小于等于的次数，由茎叶图可知成绩小于等于的有次，

∴输出结果为.

故选：A.

9．在等比数列中，有，类比上述性质，在等差数列中，有（    ）

A． B．

C． D．

【答案】D

【分析】利用等差数列角标和的性质即可得到正确选项.

【详解】选项A：在等差数列中，当且仅当公差为0时，成立.判断错误；

选项B：在等差数列中，由，可得.判断错误；

选项C：在等差数列中，由，可得.判断错误；

选项D：在等差数列中，由，可得.判断正确.

故选：D.

10．若函数的单调递减区间为，则实数k的值为（    ）

A．1 B． C．3 D．

【答案】A

【分析】求导得到导函数，确定，1是的两根，解得答案.

【详解】由，由已知递减区间，则得：，

故，1是的两根，，，

故选：A

11．已知函数在时的极值为，则函数的单调递减区间为（    ）

A． B．

C． D．

【答案】D

【分析】求导函数，利用函数在时极值为可得，解方程求出，再令即可求解.

【详解】由函数，∴，

∴，解得，∴，

令，则，解得，令，则x<0或x>2，

∴在x=2处取极值且函数的单调递减区间为.

故选：D.

12．已知对任意恒成立，其中a，b为常数且，则（    ）

A．  B．

C． D．

【答案】C

【分析】利用导数求得最小值，进而求得间的关系.

【详解】由题意知：定义域为R，，

若，则；

若，则；

∴在上单调递减，在上单调递增，

∴，

若恒成立，则，即；

综上所述：，

故选：C.

二、填空题

13．已知复数，则____.

【答案】

【分析】利用复数模的定义即可求得的值.

【详解】∵，

∴，

故答案为：.

14．函数的最小值为________.

【答案】

【分析】对函数求导，找到函数的单调区间即极值，再进一步求函数的最小值.

【详解】，当时，单调递减，当时，单调递增，

∴当时，取极小值也是最小值，∴，

故答案为：.

15．以下是标号分别为①、②、③、④的四幅散点图，它们的样本相关系数分别为，那么相关系数的大小关系为_____（按由小到大的顺序排列）.

【答案】

【分析】利用样本相关系数的性质即可判断出的大小关系

【详解】根据散点图可知，图①③成正相关，图②④成负相关，

∴，

又图①②的散点图近似在一条直线上，则图①②两变量的线性相关程度比较高，

图③④的散点图比较分散，故图③④两变量的线性相关程度比较低，

即与比较大，与比较小，∴，

故答案为：.

16．已知不等式恰有2个整数解，则实数k的取值范围为___________.

【答案】

【分析】转化为，构造函数，利用导数研究单调性可作出大致图象，数形结合即可得解.

【详解】原不等式等价于，

设，，

，令，得.

当时，，在上单调递增，

当时，，在上单调递减，

当时，取极大值1.

又，且时，

与的图象如下，

直线恒过点，

当时，显然不满足条件；

当时，只需要满足，解得，

的取值范围为，

故答案为：.

三、解答题

17．计算下列复数运算：

(1)；

(2).

【答案】(1)0

(2)1

【分析】（1）(2)利用复数运算规则即可求得

【详解】（1）；

（2）.

18．已知函数在点处的切线与直线垂直.

(1)求a的值

(2)求函数的极值.

【答案】(1)

(2)极小值 ，极大值 .

【分析】（1）求导，根据条件求出a；

（2）根据导函数的符号确定单调性，再根据单调性确定极值.

【详解】（1）易得 ，

又函数在点处的切线与直线垂直，∴ ，得；

（2）由（1）得， ，

令 有或，可得

在 处取得极大值，在 处取得极小值；

综上，极大值，极小值 .

19．每天锻炼一小时，健康生活一辈子，现在很多年轻人由于诸多原因身体都是处于“亚·健康”状态，为了了解现在的年轻人运动锻炼的状况，某社会机构做了一次调查，随机采访了100位年轻人，并对其完成的调查结果进行了统计，将他们分为男生组、女生组，把每周锻炼的时间不低于5小时的年轻人归为“健康生活”，低于5小时的年轻人归为“亚健康生活”，并绘制了如下2×2列联表.

附：

(1)能否有95%的把握认为是否为“健康生活”与年轻人的性别有关？（运算结果保留三位小数）

(2)用分层抽样的方法在健康生活的45名受采访的年轻人中选取6人参加一次公益活动，需要在这6名年轻人中随机选取两人作为这次活动的联络员，求两名联络员均为男性的概率.

【答案】(1)没有95%的把握认为是否为“健康生活”与年轻人的性别有关

(2)

【分析】（1）计算，并与表中3.841比较大小得出结果；

（2）列出6名年轻人中随机选取两人的所有基本事件，再找到两名均为男性的事件个数，求其概率即可.

【详解】（1）由，

∵3.030<3.841，

∴没有95%的把握认为是否为“健康生活”与年轻人的性别有关；

（2）易得选取参加公益活动的6人为4男2女，

用a，b，c，d，1，2表示此4男2女，则基本事件：，，，，，，，，，，，，，，共15个基本事件，

记两名联络员均为男性为事件A，事件A包含6个基本事件，

，

∴两名联络员均为男性的概率为.

20．一艘渔船在进行渔业作业的过程中，产生的主要费用有燃油费用和人工费用，已知渔船每小时的燃油费用与渔船速度的立方成正比，已知当渔船的速度为10海里/小时时，燃油费用是600元/小时，人工费用是4050元/小时，记渔船的航行速度为v（海里/小时），满足0≤v≤30，记渔船航行一个小时的主要费用为q元（主要费用=燃油费+人工费），渔船每航行1海里产生的主要费用为p元.

(1)用航行速度v（海里/小时）表示出航行一小时的主要费用q元；

(2)用航行速度v（海里/小时）表示出航行1海里产生的主要费用p元；

(3)求航行1海里产生的主要费用p（元）的最小值，及此时渔船的航行速度v（海里/小时）的大小.

【答案】(1)

(2)

(3)当航行速度为15海里/小时时，航行1海里产生的主要费用p有最小值405元

【分析】（1）设，代入数据计算得到，得到的解析式.

（2）确定，计算得到答案.

（3）求导得到单调区间，计算最值得到答案.

【详解】（1）设渔船每小时的燃油费用为y元，由题设可设，

又当渔船的速度为10海里/小时时，燃油费用是600元/小时，

得，，

航行一小时的主要费用为：；

（2）；

（3），则；

由，得到，，得到，

可得函数的增区间为，减区间为，

故当时，，

即当航行速度为15海里/小时时，航行1海里产生的主要费用p有最小值405元.

21．市场研究机构Counterpoint发布了最新全球电动汽车市场报告，2022年总计销量超1020万辆，比亚迪、特斯拉和大众集团位列排行榜前三.某电动汽车公司调研统计了之前5年（2018年到2022年）自己品牌电动汽车年销售量y（单位：万辆），并制作了如下表格.

(1)请根据表格中统计的数据作出散点图：

(2)记年份代码为x，2018年到2022年分别对应x=1，2，3，4，5，请根据散点图判断，模型①y=a+bx；②；③，哪一个更适合作为年销售量y关于年份代码x的回归方程（给出判断即可，不必说明理由）；

(3)根据（2）的判断结果，求出年销售量y关于年份代码x的回归方程，并预测今年（2023年）该公司电动汽车的年销售量.

参考数据：

参考公式：最小二乘估计公式：，.

【答案】(1)散点图见解析

(2)②更适合

(3)，96.5万辆

【分析】（1）据表格中统计的数据描点；

（2）根据散点图得出哪一个函数的模型更适合；

（3）根据最小二乘法求出回归直线方程，再代入年份代码进行估计.

【详解】（1）如图，

（2）根据散点图可知②更适合；

（3）令，则，，，，

对于回归方程，可得：，

，

∴回归方程为，即，

令x=6，得，

预测2023年该公司电动汽车的年销售量为96.5万辆.

22．已知函数.

(1)讨论函数的单调性；

(2)若是函数的两个不同极值点，且满足：，求证：.

【答案】(1)答案见解析

(2)证明见解析

【分析】（1）求出函数的导数，就、、、分类讨论导数的符号后可得函数的单调性；

（2）求出，则原不等式等价于，利用导数可证明该不等式.

【详解】（1）

可得，，

①当时，由，，

此时在上为增函数，在上为减函数；

②当时，恒成立，此时在上为增函数；

③当时，由或，，

此时在上为增函数，在上为减函数；

④当时，由或，，

此时在上为增函数，在上为减函数；

综上所述：当时，在上为增函数，在上为减函数；

当时，在上为增函数；

当时，在上为增函数，在上为减函数；

当时，在上为增函数，在上为减函数；

（2）由（1）可得：，，

，

欲证，即证，只需证，

记，，

可得，即在为减函数，

∴，即得证.

所以结论得证.

【点睛】方法点睛：利用导数研究函数的单调性的步骤：

①写定义域，对函数求导；

②在定义域内，解不等式和；

③写出单调区间.

利用导数研究解决不等式恒成立问题的常用方法：

①数形结合法；②分离参数法；③构造函数法.