初中数学人教版九年级上册24.1.1 圆优秀练习
展开2023年人教版数学九年级上册
《24.1.3 弧、弦、圆心角》同步精炼
一 、选择题
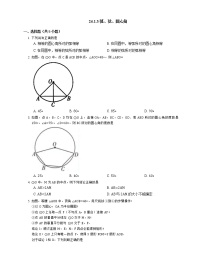
1.如图,⊙O中,=,∠ABC=70°.则∠BOC的度数为( )
A.100° B.90° C.80° D.70°
2.如图,A,B,C,D是⊙O上的四个点,∠A=60°,∠B=24°,则∠C的度数为( )
A.84° B.60° C.36° D.24°
3.下列命题中,真命题的个数是( )
①同位角相等
②经过一点有且只有一条直线与这条直线平行
③长度相等的弧是等弧
④顺次连接菱形各边中点得到的四边形是矩形.
A.1个 B.2个 C.3个 D.4个
4.如图,在⊙O中,AC∥OB,∠BAO=25°,则∠BOC的度数为( )
A.25° B.50° C.60° D.80°
5.如图,在⊙O中,若C是弧BD的中点,则图中与∠BAC相等的角有( )
A.1个 B.2 个 C.3个 D.4个
6.如图,AC是⊙O的直径,∠BAC=20°,P是弧AB的中点,则∠PAB等于( )
A.35° B.40° C.60° D.70°
7.如图,⊙O为△ABC的外接圆,∠A=72°,则∠BCO的度数为( )
A.15° B.18° C.20° D.28°
8.如图,△ABC是⊙O的内接三角形,AB=AC,∠BCA=65°,作CD∥AB,并与⊙O相交于点D,连接BD,则∠DBC的大小为( )
A.15° B.35° C.25° D.45°
9.如图,在四边形ABCD中AC,BD为对角线,AB=BC=AC=BD,则∠ADC的大小为( )
A.120° B.135° C.145° D.150°
10.如图,A、B、P是半径为2的⊙O上的三点,∠APB=45°,则弦AB的长为( )
A. B.2 C.2 D.4
二 、填空题
11.如图,在⊙O中直径CD垂直弦AB,垂足为E,若∠AOD=52°,则∠DCB=______.
12.如图,点A、B、C、D在⊙O上,OB⊥AC,若∠BOC=56°,则∠ADB=______.
13.如图,将直角三角板60°角的顶点放在圆心O上,斜边和一直角边分别与⊙O相交于A、B两点,P是优弧AB上任意一点(与A、B不重合),则∠APB=______.
14.如图,点A、B、C、D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD= .
15.AB为半圆O的直径,现将一块等腰直角三角板如图放置,锐角顶点P在半圆上,斜边过点B,一条直角边交该半圆于点Q.若AB=2,则线段BQ的长为 .
16.如图,在⊙O中,∠AOB+∠COD=70°,AD与BC交于点E,则∠AEB的度数为 .
三 、解答题
17.如图,已知AB,CG是⊙O的两条直径,AB⊥CD于点E,CG⊥AD于点F.
(1)求∠AOG的度数;
(2)若AB=2,求CD的长.
18.如图所示,已知△ABC内接于⊙O,AB=AC,∠BOC=120°,延长BO交⊙O于D点.
(1)试求∠BAD的度数;
(2)求证:△ABC为等边三角形.
19.如图,点A、B、C、D、E都在⊙O上,AC平分∠BAD,且AB∥CE.
求证:AD=CE.
20.如图,点A、B、C是圆O上的三点,AB∥OC
(1)求证:AC平分∠OAB;
(2)过点O作OE⊥AB于E,交AC于点P,若AB=2,∠AOE=30°,求圆O的半径OC及PE的长.
21.如图,AB是⊙O的直径,∠BAC=60°,D为半圆的中点,若⊙O的半径为4,求CD的长.
22.已知圆O的直径AB=12,点C是圆上一点,且∠ABC=30°,点P是弦BC上一动点,过点P作PD⊥OP交圆O于点D.
(1)如图1,当PD//AB时,求PD的长;
(2)如图2,当BP平分∠OPD时,求PC的长.
答案
1.C.
2.D
3.A
4.B.
5.C
6.A
7.B
8.A.
9.D.
10.C.
11.答案为:26°.
12.答案为:28°.
13.答案为:30°.
14.答案为:60°.
15.答案为:.
16.答案为:35°.
17.解:(1)连接OD,
∵AB⊥CD,
∴,
∴∠BOC=∠BOD,
由圆周角定理得,∠A=∠BOD,
∴∠A=∠BOD,
∵∠AOG=∠BOD,
∴∠A=∠AOG,
∵∠OFA=90°,
∴∠AOG=60°;
(2)∵∠AOG=60°,
∴∠COE=60°,
∴∠C=30°,
∴OE=OC=,
∴CE=,
∵AB⊥CD,
∴CD=2CE=.
18.解:(1)∵BD是⊙O的直径,
∴∠BAD=90°.
(2)证明:∵∠BOC=120°,
∴∠BAC=∠BOC=60°.
又∵AB=AC,
∴△ABC是等边三角形.
19.证明:如图,∵AB∥CE,
∴∠ACE=∠BAC.
又∵AC平分∠BAD,
∴∠BAC=∠DAC,
∴∠C=∠CAD,
∴=,
∴+=+,
∴=,
∴AD=CE.
20.证明:(1)∵AB∥OC,
∴∠C=∠BAC.
∵OA=OC,
∴∠C=∠OAC.
∴∠BAC=∠OAC.
即AC平分∠OAB.
(2)∵OE⊥AB,
∴AE=BE=AB=1.
又∵∠AOE=30°,∠PEA=90°,
∴∠OAE=60°.OA=2,
∴∠EAP=∠OAE=30°,
∴PE=,
即PE的长是.
21.解:连接AD、OD、OC,过A作AE⊥CD于E,
∵D为半圆的中点,AB为⊙O的直径,
∴∠AOD=90°,
∵AO=OD=4,
∴AD=4,∠ADO=45°,
∵OC=OA,∠BAC=60°,
∴△ACO是等边三角形,
∴AC=AO=4,∠AOC=60°,
∴∠COD=60°+90°=150°,
∵OC=OD,
∴∠OCD=∠ODC=15°,
∴∠ADC=∠ADO﹣∠ODC=45°﹣15°=30°,
∵∠ACO=60°,∠OCD=15°,
∴∠ACE=45°,
∴△ACE是等腰直角三角形,
∴CE=2.
∴CD=CE+ED==2+2.
22.解:如图1,连接OD .
∵直径AB=12
∴OB=OD=6
∵PD⊥OP
∴∠DPO=90°
∵PD∥AB
∴∠DPO+∠POB=180°
∴∠POB=90°
又∵∠ABC=30°,OB=6
∴OP=2,
∵在Rt△POD 中,PO2+PD2=OD2
∴PD=2.
(2)如图2,过点O 作OH⊥BC,垂足为H
∵OH⊥BC
∴∠OHB=∠OHP=90°
∵∠ABC=30°,OB=6
∴OH=3,BH=3,
∵在⊙O 中,OH⊥BC
∴CH=BH=3.
∵BP 平分∠OPD
∴∠BPO=∠DPO=45°,
∴PH=3
∴PC=CH﹣PH=3﹣3.
初中数学人教版九年级上册24.1.1 圆课堂检测: 这是一份初中数学人教版九年级上册24.1.1 圆课堂检测,共2页。试卷主要包含了下列命题中,正确的有,下列说法中,正确的是,下列命题中,不正确的是,如果两个圆心角相等,那么,已知,如果两条弦相等,那么等内容,欢迎下载使用。
数学24.1.1 圆练习题: 这是一份数学24.1.1 圆练习题,共2页。试卷主要包含了导学过程,课堂练习,课堂小结,反馈检测等内容,欢迎下载使用。
初中数学人教版九年级上册24.1.1 圆同步达标检测题: 这是一份初中数学人教版九年级上册24.1.1 圆同步达标检测题,共3页。试卷主要包含了圆心角的概念,有关弧、弦、圆心角关系的定理,定理的推论等内容,欢迎下载使用。