2022-2023学年四川省广安市第二中学校高二下学期期中考试数学试题（文）含解析

这是一份2022-2023学年四川省广安市第二中学校高二下学期期中考试数学试题（文）含解析，共15页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
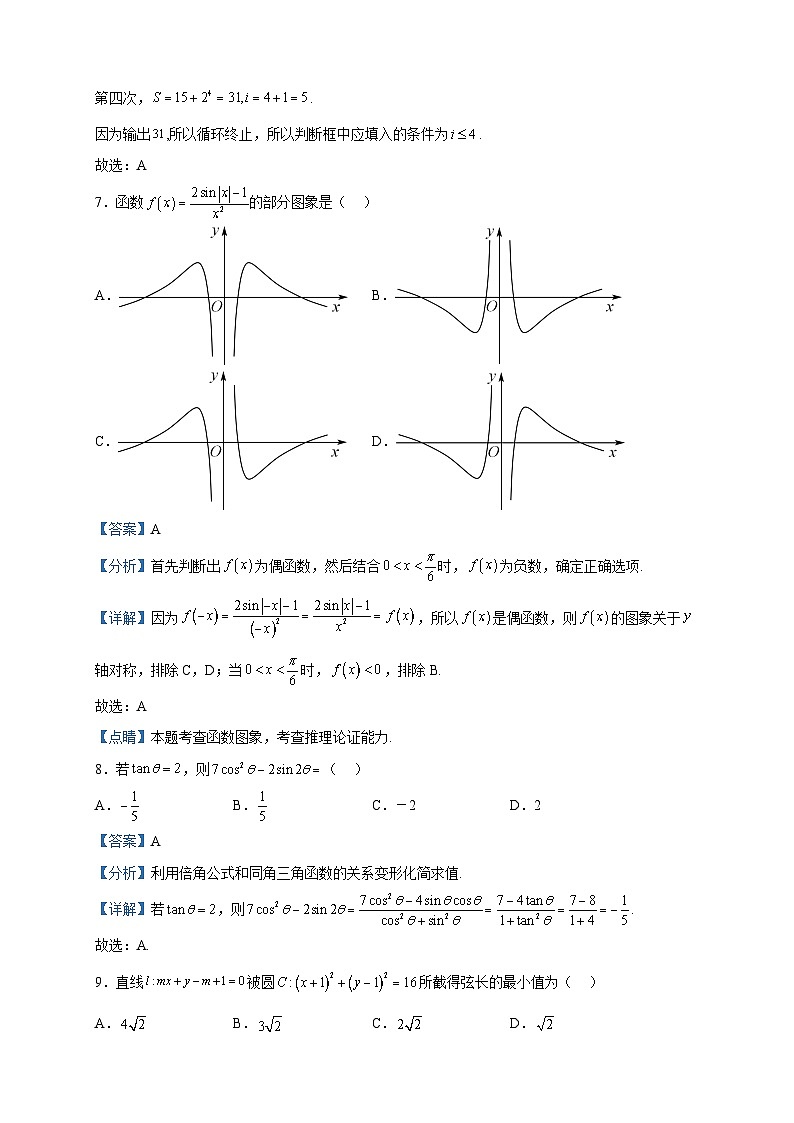
2022-2023学年四川省广安市第二中学校高二下学期期中考试数学试题（文） 一、单选题1．设命题p：，，则为（   ）A．， B．，C．， D．，【答案】B【分析】根据特称量词命题的否定为全称量词命题即可求解.【详解】p：，，则：，，故选:B2．复数等于（ ）A．１+ｉ B．１－ｉ C．－１+ｉ D．－１－ｉ【答案】A【详解】，选A 3．命题是命题的（   ）A．充分不必要条件 B．必要不充分条件C．充分必要条件 D．既不充分又不必要条件【答案】B【分析】解不等式，利用集合的包含关系判断可得出结论.【详解】解不等式得，因为，所以，是的必要不充分条件.故选：B.4．等差数列的前n项和为，若公差，，为与的等比中项，则：（    ）A．15 B．21 C．30 D．42【答案】A【分析】根据已知条件列出关于首项与公差的方程组，解出与的值，即可计算出【详解】由题意得，由，解得，.故选：A5．四川乐山沙湾区是一个人杰地灵的好地方，大文豪郭沫若先生就出生于此地.乐山沫若中学高二（7）班文学小组的同学们计划在郭老先生的5部历史剧《屈原》《凤凰涅槃》《孔雀胆》《蔡文姬》《高渐离》中，随机选两部排练节目参加艺术节活动，则《风凰涅槃》恰好被选中的概率为（    ）A． B． C． D．【答案】B【分析】对5部历史剧编号，利用列举法求出概率作答.【详解】记5部历史剧《屈原》《凤凰涅槃》《孔雀胆》《蔡文姬》《高渐离》分别为a，b，c，d，e，从5部历史剧中随机选两部的试验含有的基本事件有：，共10个结果，《风凰涅槃》恰好被选中的事件含有的基本事件有：，共4个结果，所以《风凰涅槃》恰好被选中的概率.故选：B6．执行如图所示的程序框图，为使输出的数据为31，则判断框中应填入的条件为（      ）A． B． C． D．【答案】A【分析】根据程序框图循环结构计算得到，结合输出的结果为31，从而确定填入的条件为.【详解】第一次，； 第二次，;第三次，; 第四次，.因为输出,所以循环终止，所以判断框中应填入的条件为.故选：A7．函数的部分图象是（    ）A． B．C． D．【答案】A【分析】首先判断出为偶函数，然后结合时，为负数，确定正确选项.【详解】因为，所以是偶函数，则的图象关于轴对称，排除C，D；当时，，排除B.故选：A【点睛】本题考查函数图象，考查推理论证能力.8．若，则（    ）A． B． C．－2 D．2【答案】A【分析】利用倍角公式和同角三角函数的关系变形化简求值.【详解】若，则.故选：A.9．直线被圆所截得弦长的最小值为（    ）A． B． C． D．【答案】A【分析】先判断直线与圆的位置关系，再由圆心与直线过的定点与直线垂直求解.【详解】解：易知直线l过定点，圆心，因为，所以直线l与圆C相交，当时，l被圆C所截得的弦最短，此时弦长．故选：A．10．已知，，直线与曲线相切，则的最小值是（    ）A．16 B．12 C．8 D．4【答案】D【分析】根据导数的几何意义结合已知方程求出的关系，再根据不等式中“1”的整体代换即可得出答案.【详解】对求导得，由得，则，即，所以，当且仅当时取等号．故选：D．11．已知函数对任意的满足（其中是函数的导函数），则下列不等式成立的是（        ）A． B．C． D．【答案】C【分析】根据条件构造函数，，求函数的导数，确定函数的单调性，利用单调性比较函数值大小即可逐项判断，即可得到结论．【详解】构造函数，，则，所以在上单调递增，则，所以，即，故A不正确；则，所以，即，故B不正确；则，所以，即，故C正确；则，所以，即，故D不正确.故选：C.12．已知抛物线的焦点为，准线为，过的直线与交于两点（点在第一象限），与交于点，若，，则（    ）A． B．3 C．6 D．12【答案】B【分析】利用抛物线的定义，以及几何关系可知，再利用数形结合表示的值，进而得，再根据焦半径公式得，，进而求解直线的方程并与抛物线联立得，再用焦半径公式求解即可.【详解】如图，设准线与轴的交点为，作，，垂足分别为，，所以，.又，所以，设，则.因为，所以，所以，所以，即.所以，抛物线为，焦点为，准线为，由得，解得，所以，，所以，直线的方程为所以，联立方程得，解得，所以，，所以， 故选：B 二、填空题13．某高中的三个年级共有学生2000人，其中高一600人，高二680人，高三720人，该校现在要了解学生对校本课程的看法，准备从全校学生中抽取50人进行访谈，若采取分层抽样，且按年级来分层，则高一年级应抽取的人数是______．【答案】15【分析】根据分层抽样原则直接计算即可【详解】由题意，从全校2000人中抽取50人访谈，按照年级分层，则高一年级应该抽人.故答案为：1514．若实数x，y满足约束条件，设，则t的最大值为__________.【答案】5【分析】画出满足条件的平面区域，求出A点的坐标，将t=2x+y转化为y=﹣2x+t，结合函数图象求出t的最大值即可．【详解】画出满足条件的平面区域，如图示：，由，解得：A（2,1），由t=2x+y得：y=﹣2x+t，显然直线y=﹣2x+t过A（2,1）时，t最大，故t的最大值是：t=4+1=5.故答案为：5．15．平面向量满足,,则与的夹角为______.【答案】【分析】将两边平方,再将,代入,即可求得夹角.【详解】解:由题知,所以两边平方可得,化简可得,即,即,因为与的夹角范围为:,所以与的夹角为.故答案为:16．已知，对，且，恒有，则实数的取值范围是__________.【答案】【分析】根据对条件 做出的解释构造函数，利用函数的单调性求解.【详解】对，且，恒有，即 ，所以函数 是增函数，设 ，则在上单调递增，故 恒成立，即，设 ，当时， ，函数单调递增；当时， ，函数单调递减；故，即；故答案为： . 三、解答题17．为庆祝党的二十大的胜利召开，培养担当民族复兴的时代新人，某高校在全校开展“不负韶华，做好社会主义接班人”的宣传活动．为进一步了解学生对党的“二十大”精神的学习情况，学校开展了“二十大”相关知识的竞赛活动，现从参加该活动的学生中随机抽取100人，将他们的竞赛成绩（满分为100分）分为5组：，，，，，得到如图所示的频率分布直方图：(1)估计这100名学生的竞赛成绩的中位数（结果保留整数）；(2)在抽取的100名学生中，规定：竞赛成绩不低于70分为“优秀”，竞赛成绩低于70分为“非优秀”．请将下面的2×2列联表补充完整，并判断是否有99%的把握认为“竞赛成绩是否优秀与性别有关”？（精确到0.001） 优秀非优秀合计男 30 女  50合计  100参考公式及数据：，其中．0.100.050.0250.0100.0050.0012.7063.8415.0246.6357.87910.828 【答案】(1)中位数为72(2)表格见解析，有99%的把握认为“竞赛成绩是否优秀与性别有关”． 【分析】（1）运用频率分布直方图中位数计算公式可求得结果.（2）计算出优秀人数完成列联表，再运用独立性检验判断即可.【详解】（1）因为，所以竞赛成绩的中位数在内．设竞赛成绩的中位数为m，则，解得，所以估计这100名学生的竞赛成绩的中位数为72．（2）由（1）知，在抽取的100名学生中，竞赛成绩为“优秀”的有：人，由此可得完整的2×2列联表： 优秀非优秀合计男203050女401050合计6040100零假设：竞赛成绩是否优秀与性别无关.因为，所以有99%的把握认为“竞赛成绩是否优秀与性别有关”．18．已知的角，，的对边分别为，，，满足.(1)求；(2)若，求周长的取值范围.【答案】(1)(2) 【分析】（1）利用正弦定理和余弦定理化简已知条件，由此求得正确答案.（2）将表示为角的形式，然后利用三角函数值域的求法求得正确答案.【详解】（1）因为，由正弦定理得，即，由余弦定理得，所以.（2）依题意，.由正弦定理，即周长，∵，∴，，，所以周长的取值范围.19．图甲所示的平面五边形中，，，，，，现将图甲所示中的沿边折起，使平面平面得如图乙所示的四棱锥．在如图乙所示中．(1)求证：平面．(2)求三棱锥的体积．【答案】(1)证明见解析；(2). 【分析】（1）先证明，再由面面垂直的性质得出平面，再得出，再由线面垂直的判定定理得证；（2）证明是三棱锥的高，再由体积公式计算即可.【详解】（1），平面平面，是交线，平面，平面又平面，又，平面，平面.（2）取中点，连接，如图，由，可知，又平面平面，是交线，平面，平面，即三棱锥的高为，由，，知，由知，,,.20．若椭圆过抛物线的焦点，且与双曲线有相同的焦点．(1)求椭圆E的方程；(2)不过原点O的直线与椭圆E交于A、B两点，求面积的最大值以及此时直线l的方程．【答案】(1)(2)面积的最大值为，此时直线的方程为 【分析】(1)根据抛物线和双曲线的性质结合椭圆的的关系求解；(2)利用韦达定理求出弦长，再利用点到直线距离公式为三角形的高即可求解.【详解】（1）抛物线的焦点为，所以，因为双曲线的焦点坐标为，所以则，所以椭圆E的方程为.（2）设，联立可得，因为直线与椭圆E交于A、B两点，所以解得，由韦达定理可得，由弦长公式可得，点到直线的距离为，所以当且仅当即时取得等号，所以面积的最大值为，此时直线的方程为.21．已知函数.(1)讨论函数的单调性；(2)若，函数在上恒成立，求整数的最大值.【答案】(1)见解析(2) 【分析】（1）求导后分解因式，分类讨论即可得到函数的单调性；（2）由题意求出，转化为在上恒成立，利用导数求出的最小值，即可求解.【详解】（1）（1）若时，，在上单调递增；若时，，当或时，，为增函数，当时，，为减函数，若时，，当或时，，为增函数，当时，，为减函数.综上，时，在上单调递增；当时，在和上单调递增，在上单调递减；当时，在和上单调递增，在上单调递减.（2）由，解得 ，所以，由时，，可知在上恒成立可化为在上恒成立，设，则，设，则 ，所以在上单调递增，又，，所以方程有且只有一个实根，且 ，，所以在上，， 单调递减，在上，，单调递增，所以函数的最小值为，从而，又为整数，所以的最大值为：.【点睛】解答本题的难点在于得到后，不能求出的零点，需要根据的单调性及零点存在定理得到的大致范围，再利用的范围及求解即可.22．在平面直角坐标系中，直线l的参数方程为（t为参数）．以原点为极点，x轴的非负半轴为极轴建立极坐标系，曲线C的极坐标方程为．(1)求直线l的极坐标方程和曲线C的直角坐标方程；(2)设点，直线l与曲线C交于点A，B．求证：．【答案】(1)，(2)证明见解析. 【分析】（1）直接利用转换关系式，把参数方程直角坐标方程和极坐标方程之间进行转换.（2）利用一元二次方程根和系数的关系求出结果.【详解】（1）将直线l的参数方程（t为参数）化为普通方程为．∵∴直线l的极坐标方程为∴由曲线C的极坐标方程    化为直角坐标方程为.（2）将代入得设点A、B对应的参数为，则∵∴.∴.