2022-2023学年黑龙江省哈尔滨市第一二二中学校高二下学期期中数学试题含解析

2022-2023学年黑龙江省哈尔滨市第一二二中学校高二下学期期中数学试题

一、单选题

1．在复平面内，复数z对应的点为，则（    ）

A．1 B．i C．－i D．

【答案】B

【分析】根据复数的几何意义可得，根据复数除法运算即可求解.

【详解】由题意可得，故，

故选：B.

2．1至9中的质数能够组成没有重复数字的整数的个数为（    ）

A．24 B．36 C．48 D．64

【答案】D

【分析】先得出1至9中的质数2，3，5，7，再排列组合即可.

【详解】由题意得1至9中的质数为2，3，5，7四个数，故能组成的无重复数字的整数有：，即D正确.

故选：D

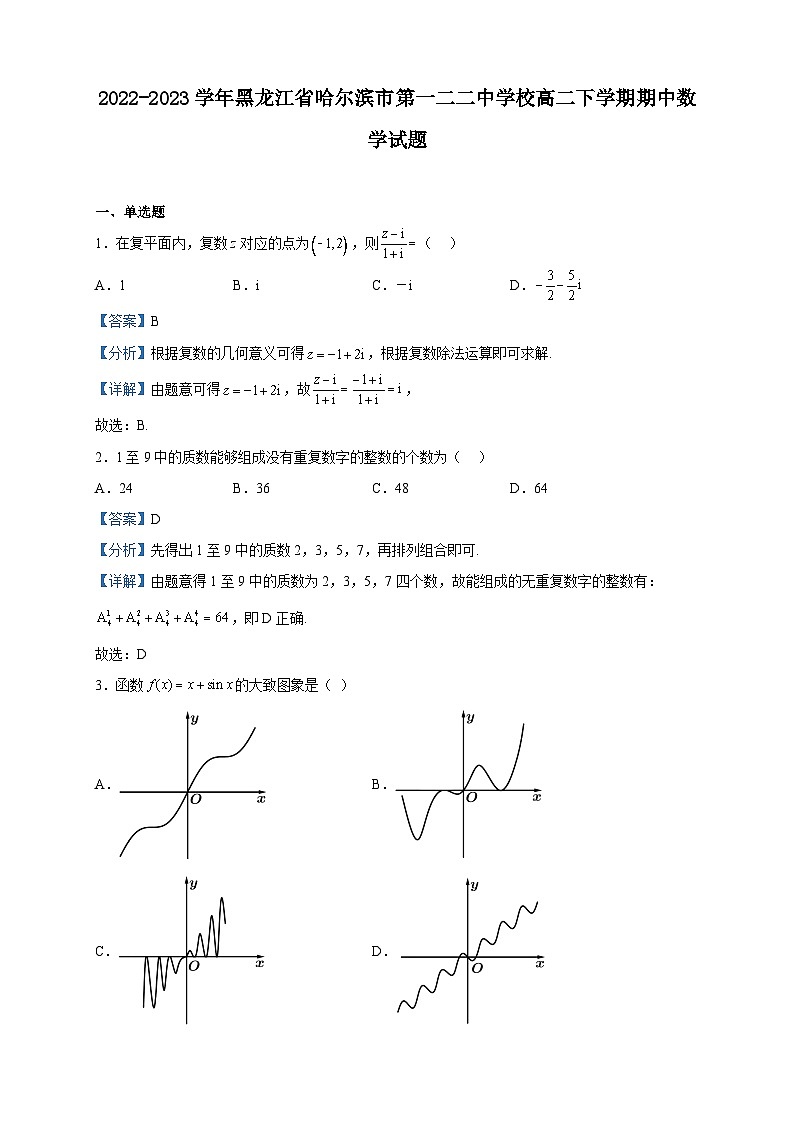
3．函数的大致图象是（ ）

A． B．

C． D．

【答案】A

【分析】判断函数的奇偶性，通过求导判断函数的单调性，利用排除法即可得解．

【详解】因为，所以是奇函数，

从而的图像关于原点对称.故排除B和C.

因为，所以是增函数，故排除D.

故选：．

4．若函数有两个极值点且这两个极值点互为倒数，则（    ）

A． B． C． D．

【答案】B

【分析】先求函数的导函数，根据极值点互为倒数应用韦达定理，

得出，即可求出导函数的值.

【详解】，

函数的极值点即方程的两个实根，

由题意可知，两实根互为倒数，则，解得，

所以，故，

故选：.

5．为提升学生的数学素养，某中学特开设了“数学史”、“数学建模”、“古今数学思想”、“数学探究”、“中国大学先修课程微积分学习指导”五门选修课程，要求每位同学每学年至多选四门，高一到高二两学年必须将五门选修课程选完，则每位同学不同的选修方式为（    ）

A． B． C． D．

【答案】A

【分析】将五门课程分为两组，每组的数量分别为、或、，然后将这两组课程分配给高一、高二两个学年，利用组合计数原理结合分步乘法计数原理可得结果.

【详解】将五门课程分为两组，每组的数量分别为、或、，

然后将这两组课程分配给高一、高二两个学年，

所以，每位同学不同的选修方式种数为.

故选：A.

6．定义运算：，将函数的图像向左平移个单位，所得图像对应的函数为偶函数，则的可能取值是（    ）

A． B． C． D．

【答案】C

【分析】根据三角函数图象的变换求得变换后的解析式，再根据偶函数的定义求解.

【详解】由题可知，，

将的图像向左平移个单位，所得函数为，

因为所得图像对应的函数为偶函数，

所以，解得，

因为，所以

故选:C.

7．根据以往经验，一超市中的某一商品每月的销售量(单位：件)与销售价格(单位：元/件)满足关系式，其中.已知该商品的成本为20元/件，则该超市每月销售该商品所获得利润的最大值为（    ）

A．8600元 B．8060元 C．6870元 D．4060元

【答案】B

【分析】根据已知销售价格列出利润函数，然后利用导数求得最大值．

【详解】设超市每月销售该商品所获得的利润为元，

则，，

，

令，得，则在上单调递增；令，得，则在上单调递减.所以的最大值为.

故选：B．

8．设，，，则，，的大小关系是（    ）

A． B．

C． D．

【答案】C

【分析】根据三个式子的结构，构造函数，求导判断单调性，进而比较，，的大小，即可得，，的大小关系.

【详解】令，则，

，，

由可得且，

由可得；所以在上单调递减，

因为，所以，

所以，

故选：C.

二、多选题

9．等差数列的公差为，前项和为，当首项和变化时，是一个定值，则下列各数也为定值的有

A． B． C． D．

【答案】BC

【解析】根据等差中项的性质和等差数列的求和公式可得出结果.

【详解】由等差中项的性质可得为定值，则为定值，为定值，但不是定值.

故选：BC.

【点睛】本题考查等差中项的基本性质和等差数列求和公式的应用，考查计算能力，属于基础题.

10．(多选)若双曲线C的一个焦点F(5，0)，P是双曲线上一点，且渐近线方程为yx，则下列结论正确的是（    ）

A．C的方程为=1 B．C的离心率为

C．焦点到渐近线的距离为3 D． 的最小值为2

【答案】AD

【解析】由双曲线C的一个焦点F(5，0)，且渐近线方程为yx，可得双曲线C的，再根据双曲线的性质对每一个选项进行逐一判断即可.

【详解】双曲线C的一个焦点F(5，0)，且渐近线方程为yx，

可得，焦点坐标在x轴上，所以，

由，所以，

所以C的方程为=1，A正确；

离心率为e =，B不正确；

焦点到渐近线的距离为d==4，C不正确；

的最小值为，D正确.

故选：AD

11．如图，平面平面ABEF，四边形ABCD是正方形，四边形ABEF是矩形，若G是EF的中点，，，则（    ）

A． B．平面ABCD

C． D．三棱锥外接球的表面积是

【答案】BCD

【分析】利用已知结合数量积的运算求解可判断选项A，由线面平行的判定定理可判断选项B,由面面垂直的性质定理可判断选项C,计算可得为直角三角形，再由为直角三角形，可知为三棱锥的外接球的直径，再由球的表面积公式可判断选项D．

【详解】解：，，

，

又、、两两相互垂直，

，A错误，

四边形ABEF是矩形，

平面ABCD, 平面ABCD,

平面ABCD, B正确，

平面平面ABEF，四边形ABCD是正方形，,平面平面ABEF，

平面ABEF, 平面ABEF ,,C正确，

，，

， 为直角三角形，

又为直角三角形，为三棱锥的外接球的直径，

则三棱锥的外接球的表面积．

故选：BCD．

12．现有带有编号1、2、3、4、5的五个球及四个不同的盒子，则下列表述正确的有（    ）

A．全部投入4个不同的盒子里，共有种放法

B．全部投入2个不同的盒子里，每盒至少一个，共有种放法

C．将其中的4个球投入4个盒子里的一个（另一个球不投入），共有种放法

D．全部投入4个不同的盒子里，没有空盒，共有种不同的放法

【答案】ACD

【分析】对于A，利用分步乘法计数原理计算可判断A正确；对于B，先将5个球分为2组，再全排，计算可判断B不正确；对于C，利用分步乘法计数原理计算可判断C正确；对于D，先将5个球分为4组，再全排，计算可判断D正确；

【详解】对于A，带有编号1、2、3、4、5的五个球，全部投入4个不同的盒子里，共有种放法，故A正确；

对于B，带有编号1、2、3、4、5的五个球全部投入2个不同的盒子里，第一步选2个盒子有种选法，第二步将5个球分为两组，若两组球个数之比为1：4有种分法；若两组球个数之比为2：3有种分法，第三步将两组排给两个盒子有种排法，因此共有，故B不正确；

对于C，带有编号1、2、3、4、5的五个球，将其中的4个球投入4个盒子里的一个（另一个球不投入），第一步选4个球有种选法，第二步选一个盒子有种选法，共有种放法，故C正确；

对于D，带有编号1、2、3、4、5的五个球，全部投入4个不同的盒子里，没有空盒，第一步将5球分成2：1：1：1的四组共有种分法，第二步分给四个盒子有种排法，故共有种放法，故D正确；

故选：ACD.

13．对于函数，下列说法正确的是（    ）

A． B．在处取得极大值

C．有两个不同的零点 D．若在上恒成立，则

【答案】ABD

【分析】利用导数研究函数的单调性，结合极值的定义判断选项AB；由函数零点的定义可判断选项C；构造函数，利用导数求函数的最大值，可判断D.

【详解】对于函数，，

，；

令，得，解得，

当时，，所以函数在上为单调递增函数，

当时，，所以函数在,上为单调递减函数，

∴，又，

∴，故A正确；

所以函数在处取得极大值，故B正确；

因为时，得，解得，所以函数只有一个零点，选项C错误；

因为在上恒成立，则在上恒成立，

令，则，

令，解得，

当时，，单调递增，当时，，则单调递减，

所以当时，，所以，选项D正确.

故选：ABD.

14．“杨辉三角”是二项式系数在三角形中的一种几何排列，在中国南宋数学家杨辉1261年所著的《详解九章算法》一书中就有出现.如图所示，在“杨辉三角”中，除每行两边的数都是1外，其余每个数都是其“肩上”的两个数之和，例如第4行的6为第3行中两个3的和.则下列命题中正确的是（    ）

A．在“杨辉三角”第9行中，从左到右第7个数是84

B．由“第行所有数之和为”猜想：

C．在“杨辉三角”中，当时，从第2行起，每一行的第3列的数字之和为286

D．在“杨辉三角”中，第行所有数字的平方和恰好是第行的中间一项的数字

【答案】ABCD

【分析】根据给定的“杨辉三角”，结合二项式定理、组合数计算、组合数的性质逐项分析计算判断作答.

【详解】在“杨辉三角”第9行中，从左到右第7个数是，A正确；

由“第行所有数之和为”猜想：，

因为，则令得：，B正确；

在“杨辉三角”中，当时，从第2行起，每一行的第3列的数字之和为：

，C正确；

在“杨辉三角”中，第行所有数字的平方和恰好是第行的中间一项的数字，

即

因为

对应相乘可得的系数为，

而二项式展开式的通项公式，当时，，

则的系数为：，所以，D正确.

故选：ABCD

三、填空题

15．抛物线的焦点坐标为______．

【答案】(1，0)

【分析】将抛物线化为标准方程，根据定义求得焦点坐标.

【详解】抛物线标准方程为：

焦点坐标为：

【点睛】本题考查根据抛物线方程求焦点的问题，关键是要将方程化为标准方程的形式，属于基础题.

16．哈尔滨市第一二二中学高二数学组织华容道大赛，七名数学老师依次登场，在安排出场顺序时，三个班主任需要排在一起登场，这样出场顺序一共有__________种．（用数字作答）

【答案】720

【分析】利用捆绑法即可求解.

【详解】利用捆绑法，共有种安排方法，

故答案为:720.

17．已知的展开式中所有二项式系数之和是64，则它展开式中x2的系数___________.

【答案】

【分析】利用二项式定理系数的性质，求出n，然后通过二项式定理的通项公式求出项即可．

【详解】解：的展开式的二项式系数之和为64，所以，所以，由二项式定理的通项公式得：

当时，展开式中项的系数为：

故答案为：.

18．已知函数，其中，若对于任意的，且，都有成立，则实数a的取值范围是_____________．

【答案】

【分析】根据题意转化为对任意的恒成立，令，进而转化为恒成立，得到在恒成立，令，利用导数求得函数为单调区间和最小值，得到，即可求解.

【详解】由对于任意的 ，且，都有，

则对于任意的恒成立，

令，则不等式等价于对于任意的恒成立，

即在区间单调递增，

又由，可得，

则，即在恒成立，

即在恒成立，即在恒成立，

令，可得恒成立，

所以函数为单调递增函数，所以，

则，解得，所以实数的取值范围是.

故答案为：.

【点睛】知识方法：对于已知函数的单调性求参数问题：

（1）已知可导函数在区间上单调递增，转化为区间上恒成立；

（2）已知可导函数在区间上单调递减，转化为区间上恒成立；

（3）已知可导函数在区间上存在增区间，转化为在区间上有解；

（4）已知可导函数在区间上存在减区间，转化为在区间上有解.

四、解答题

19．已知，函数.

（1）当时，求函数在点处的切线方程；

（2）若函数在区间上是减函数，求的取值范围.

【答案】（1）；（2）.

【解析】（1）求出在处的导数，即切线斜率，求出，即可求出切线方程；

（2）可得在恒成立，由此可建立关系求解.

【详解】，

（1）当时，，

，

在点处的切线方程为，即.

（2）函数在区间上是减函数，

在恒成立，

而在恒成立，

在恒成立，这时，

当函数在区间上是减函数时，.

20．在中，分别为内角A，B，C的对边，且．

（1）求C的大小；

（2）若，求的面积．

【答案】（1）；（2）．

【分析】（1）先利用正弦定理将转化为，再利用两角和的正弦公式化简可求得答案；

（2）由余弦定理结合已知条件可求出，，然后利用三角形的面积公式可求得结果

【详解】解：（1）∵，

∴根据正弦定理可得，

，

∴，

∴．因为，

∴，又

∴．

（2）由余弦定理，得，

解得，由得

所以的面积

所以的面积．

21．如图，在四面体中，，平面，点M为棱的中点，，.

（Ⅰ）求直线与所成角的余弦值；

（Ⅱ）求平面和平面的夹角的余弦值.

【答案】（Ⅰ）；（Ⅱ）.

【解析】（Ⅰ）以A为原点，分别以，，的方向为x轴，y轴，z轴的正方向的空间直角坐标系,利用空间向量的夹角公式可求得结果；

（Ⅱ）利用两个平面的法向量可求得结果.

【详解】依题意，可以建立以A为原点，分别以，，的方向为x轴，y轴，z轴的正方向的空间直角坐标系（如图），可得，，，，

（Ⅰ）依题意，．

，

所以直线与所成角的余弦值为.

（Ⅱ）易知，为平面的一个法向量，

依题意，可得，．

设为平面的法向量，则即，

不妨令，可得．

因此有，

由图可知平面和平面的夹角为锐角，

所以平面和平面的夹角的余弦值为．

【点睛】关键点点睛：建立空间直角坐标系，利用空间向量求解是解题关键.

22．已知数列满足：.

(1)求的通项公式；

(2)若数列是等比数列，且，求关于的表达式.

【答案】(1)

(2)

【分析】（1）根据等差数列的定义判断得数列是等差数列，计算公差，再写出通项公式即可；

（2）根据（1）写出数列的通项公式，再根据等比数列计算公比，写出等比数列的通项公式，两式相等即可得关于的表达式.

【详解】（1）

所以数列是等差数列，

设其公差为，则，

.

所以数列的通项公式为.

（2）由（1）知.

因为数列是等比数列，且，

数列的公比，

由等比数列的通项公式可得

，

23．已知函数．

(1)讨论的单调性；

(2)若方程有两个不同的实数根，求的取值范围．

【答案】(1)答案见解析

(2)

【分析】（1）对求导，分类讨论和时的正负，即可得出的单调性；

（2）解法一：“方程有两个不同的实数根”等价于“函数有两个零点”．对求导，讨论的单调性和最值，即可得出答案；解法二：由方程得，转化为与的图象有两个交点，对求导，得出的单调性和最值即可得出答案.

【详解】（1）由条件知，，

当时，在上恒成立，所以在单调递增．

当时，令，得，令，得，

所以在上单调递减，在上单调递增．

（2）解法一：由方程得，“方程有两个不同的实数根”等价于“函数有两个零点”．

，．

①当时，，在上是增函数，最多只有一个零点，不符合题意；

②当时，由得，

当时，，在上单调递增，当时，，在上单调递减．

（ⅰ）若，则，最多只有一个零点；

（ⅱ）若，因为，且，，

所以在区间内有一个零点．

令函数，则，．

当时，，在上是增函数；

当时，，在上是减函数.

所以，故．

所以，又，

所以在区间内有一个零点．

综上可知：当时，有两个零点，即方程有两个不同的实数根，

故a的取值范围为．

解法二：由方程得．

设函数，则，．

令，得，设，

则当时，，当时，，

所以在上单调递增，在上单调递减，

所以的极大值也就是最大值为，

且当，x趋近于0时，趋近于负无穷，当趋近于正无穷时，，且趋近于0．

方程有两个不同的实数根，转化为直线与的图象有两个交点，

结合函数图象可知a的取值范围是．