2023年北京市朝阳区中考二模数学试题(无答案)

北京市朝阳区九年级综合练习（二）

数学试卷                       2023．5

学校______ 班级______ 姓名______ 考号______

考生须知

1．本试卷共8页，共三道大题，28道小题，满分100分．考试时间120分钟．

2．在试卷和答题卡上认真填写学校名称、班级、姓名和考号．

3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效．

4．在答题卡上，选择题、作图题用2B铅笔作答，其他试题用黑色字迹签字笔作答．

5．考试结束，请将本试卷、答题卡和草稿纸一并交回．

一、选择题（共16分，每题2分）

第1-8题均有四个选项，其中符合题意的选项只有一个．

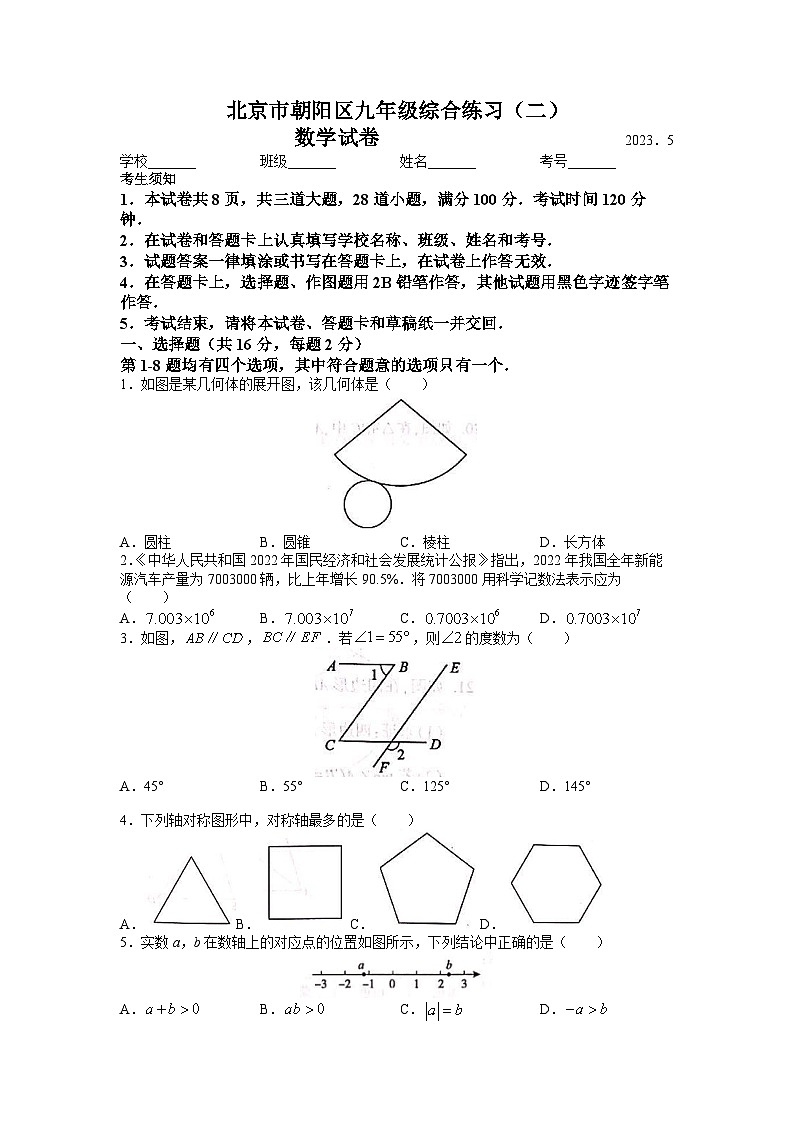
1．如图是某几何体的展开图，该几何体是（    ）

A．圆柱 B．圆锥 C．棱柱 D．长方体

2．《中华人民共和国2022年国民经济和社会发展统计公报》指出，2022年我国全年新能源汽车产量为7003000辆，比上年增长90.5%．将7003000用科学记数法表示应为（    ）

A． B． C． D．

3．如图，，．若，则的度数为（    ）

A．45° B．55° C．125° D．145°

4．下列轴对称图形中，对称轴最多的是（    ）

A．B．C．D．

5．实数a，b在数轴上的对应点的位置如图所示，下列结论中正确的是（    ）

A． B． C． D．

6．方程的解为（    ）

A． B． C． D．

7．某射箭选手在同一条件下进行射箭训练，结果如下：

下列说法正确的是（    ）

A．该选手射箭一次，估计射中靶心的概率为0.90

B．该选手射箭80次，射中靶心的频率不超过0.90

C．该选手射箭400次，射中靶心的次数不超过360次

D．该选手射箭1000次，射中靶心的次数一定为910次

8．已知点，，在反比例函数的图象上，，有下面三个结论：

①若，则；

②若，则；

③若，则．

所有正确结论的序号是（    ）

A．①② B．②③ C．①③ D．①②③

二、填空题（共16分，每题2分）

9．若分式的值为0，则x的值为______．

10．分解因式：______．

11．若关于x的一元二次方程没有实数根，则k的取值范围是______．

12．某班级准备定做一批底色相同的T恤衫，征求了全班40名同学的意向，每个人都选择了一种底色，得到如下数据：

为了满足大多数人的需求，此次定做的T恤衫的底色为______．

13．如图，平行四边形ABCD的对角线AC，BD相交于点O，E是CD的中点，则与的面积的比为______．

14．如图，AB是⊙O的直径，CD是弦，连接AC，AD．若，则______°．

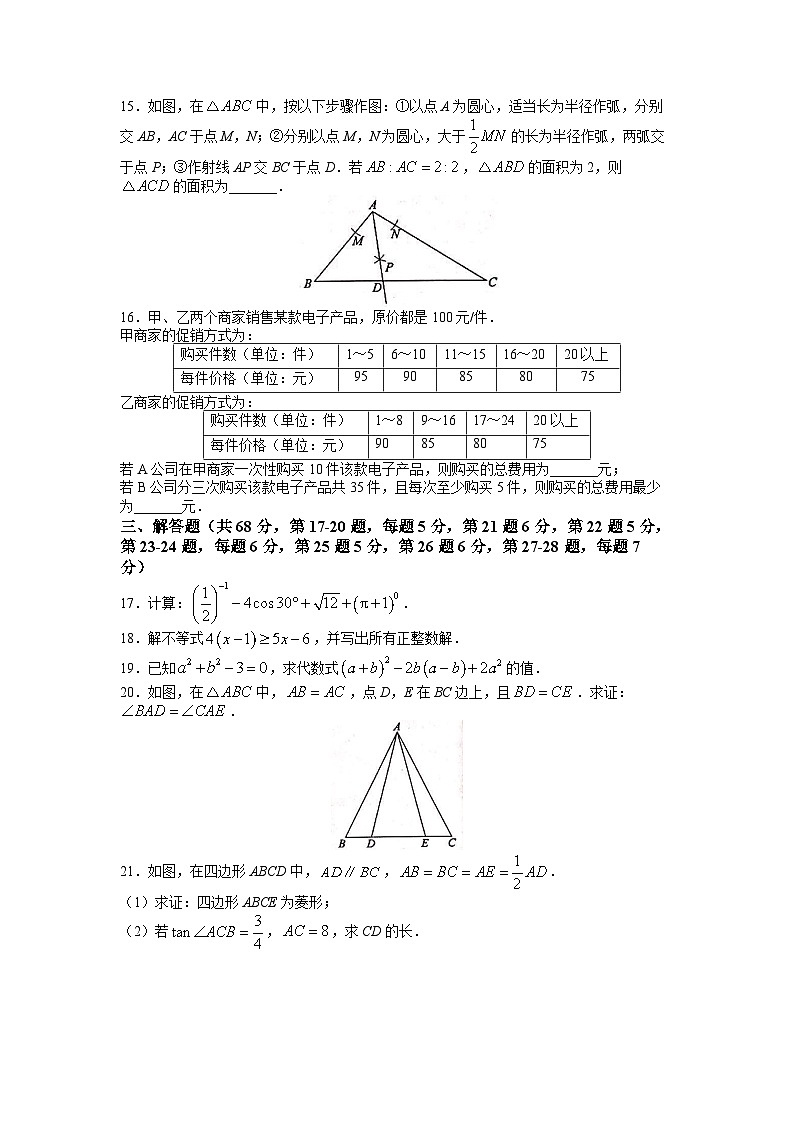
15．如图，在中，按以下步骤作图：①以点A为圆心，适当长为半径作弧，分别交AB，AC于点M，N；②分别以点M，N为圆心，大于的长为半径作弧，两弧交于点P；③作射线AP交BC于点D．若，的面积为2，则的面积为______．

16．甲、乙两个商家销售某款电子产品，原价都是100元/件．

甲商家的促销方式为：

乙商家的促销方式为：

若A公司在甲商家一次性购买10件该款电子产品，则购买的总费用为______元；

若B公司分三次购买该款电子产品共35件，且每次至少购买5件，则购买的总费用最少为______元．

三、解答题（共68分，第17-20题，每题5分，第21题6分，第22题5分，第23-24题，每题6分，第25题5分，第26题6分，第27-28题，每题7分）

17．计算：．

18．解不等式，并写出所有正整数解．

19．已知，求代数式的值．

20．如图，在中，，点D，E在BC边上，且．求证：．

21．如图，在四边形ABCD中，，．

（1）求证：四边形ABCE为菱形；

（2）若，，求CD的长．

22．在平面直角坐标系xOy中，函数的图象经过点，，与y轴交于点A．

（1）求该函数的表达式及点A的坐标；

（2）当时，对于x的每一个值，函数的值大于函数的值，直接写出m的取值范围．

23．如图，AB为⊙O的直径，C为⊙O上一点，，直线CE与直线AB相交于点H，AC平分．

（1）求证：EH是⊙O的切线；

（2）AE与的交点为F，连接FO并延长与相交于点D，连接CD．若F为中点，

求证：．

24．某校为了解本校学生每天在校体育锻炼时间的情况，随机抽取了若干名学生进行调查，获得了他们每天在校体育锻炼时间的数据（单位：min），并对数据进行了整理，描述，部分信息如下：

a．每天在校体育锻炼时间分布情况：

b．每天在校体育锻炼时间在这一组的是：

80  81  81  81  82  82  83  83  84  84  84  84  84  85  85  85  85  85  85  85  85  86  87  87  87  87  87  88  88  88  89  89  89  89  89

根据以上信息，回答下列问题：

（1）表中______，______；

（2）若该校共有1000名学生，估计该校每天在校体育锻炼时间不低于80分钟的学生的人数；

（3）该校准备确定一个时间标准p（单位：min），对每天在校体育锻炼时间不低于p的学生进行表扬．若要使25%的学生得到表扬，则p的值可以是______．

25．图1是一块铁皮材料的示意图，线段AB长为4dm，曲线是抛物线的一部分，顶点C在AB的垂直平分线上，且到AB的距离为4dm．以AB中点O为原点，建立如图2所示的平面直角坐标系．

（1）求图2中抛物线的表达式（不要求写出自变量的取值范围）；

（2）要从此材料中裁出一个矩形，使得矩形有两个顶点在AB上，另外两个顶点在抛物线上，求满足条件的矩形周长的最大值．

26．在平面直角坐标系xOy中，点在抛物线上．

（1）求的值（用含a的式子表示）；

（2）若，试说明：；

（3）点，在该抛物线上，若，，中只有一个为负数，求α的取值范围．

27．在中，，，点D在BC边上（不与点B，C重合），将线段AD绕点A顺时针旋转90°，得到线段AE，连接DE．

（1）根据题意补全图形，并证明：；

（2）过点C作AB的平行线，交DE于点F，用等式表示线段EF与DF之间的数量关系，并证明．

28．在平面直角坐标系xOy中，对于图形M给出如下定义；将M上的一点（a，b）变换为点，M上所有的点按上述变换后得到的点组成的图形记为N，称N为M的变换图形．

（1）①点的变换点的坐标为______；

②直线的变换图形上任意一点的横坐标为______；

（2）求直线的变换图形与y轴公共点的坐标；

（3）已知⊙O的半径为1，若的变换图形与直线有公共点，直接写出k的取值范围．