2023年7月浙江省普通高中学业水平考试数学押题卷（二）

2023年7月浙江省普通高中学业水平考试押题预测数学试卷（二）

一、选择题（本大题共18小题，每小题3分，共54分.每小题列出的四个备选项中只有一个是符合题目要求的，不选、多选、错选均不得分）

1．已知集合，，则（    ）

A． B． C． D．

【答案】A

【分析】直接由并集的概念求解即可.

【详解】 .

故选：A.

2．函数的定义域为（　　）

A．且 B．

C．且 D．

【答案】A

【分析】根据具体函数的定义域即可求解.

【详解】由题意得且，

解得且．

所以定义域为且.

故选：A

3．若满足，则的终边在（    ）

A．第一象限 B．第二象限 C．第三象限 D．第四象限

【答案】C

【分析】直接由各象限三角函数的符号判断即可.

【详解】由可知的终边在第三象限或第四象限，又，则的终边在第三象限.

故选：C.

4．已知数据，，，，的方差为，则数据，，，，的标准差为（   ）

A． B． C．  D．

【答案】C

【分析】根据线性变化前后数据的方差的关系求解．

【详解】由题意新数据的方差为，因此标准差为．

故选：C．

5．已知，，O为坐标原点，若，则点B的坐标应为（    ）

A．  B．

C． D．

【答案】B

【分析】根据向量的坐标运算即可求解.

【详解】,所以,

所以,

故选：B

6．（    ）

A． B． C． D．

【答案】A

【分析】直接利用余弦二倍角公式计算可得答案.

【详解】.

故选：A.

7．已知事件A､B相互独立，，则（    ）

A．0.58 B．0.9 C．0.7 D．0.72

【答案】A

【分析】由概率加法公式求解

【详解】由题意

故

故选：A

8．在中， 内角所对的边分别为， 若， 则（    ）

A． B． C． D．

【答案】B

【分析】由正弦定理进行边化角，进而求出角A，再结合余弦定理即可求得答案.

【详解】由正弦定理可知，，易知，则，而，则或，再由余弦定理可得或.

故选：B.

9．已知、、是三条不同的直线，、是不同的平面，则的一个充分条件是（　　）

A．，，且 B．， ，且，

C．，，，且 D．，，且

【答案】D

【分析】利用空间线面位置关系逐项判断可得出合适的选项.

【详解】对于A选项，，，且，则、平行或相交（不一定垂直），A不满足条件；

对于B选项，， ，且，，则、平行或相交（不一定垂直），B不满足条件；

对于C选项，，，，且，则、平行或相交（不一定垂直），C不满足条件；

对于D选项，且，则，，则，D满足条件.

故选：D.

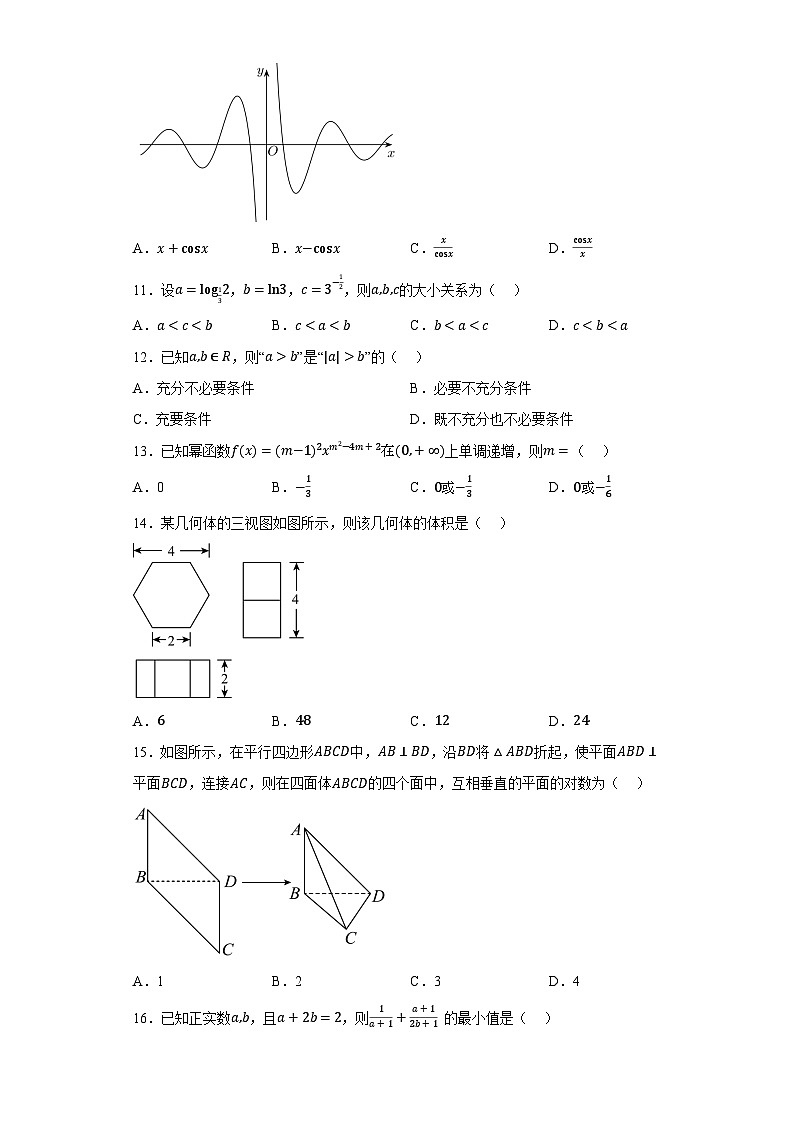
10．已知函数的部分图象如图所示，则的解析式可能是（    ）

A． B． C． D．

【答案】D

【分析】根据函数图象，可得函数在处无定义，且关于原点对称，即可判断；

【详解】解：由图可知函数的定义域中不含，且函数图象关于原点对称，

与的定义域均为，不符合题意，故A、B错误；

对于C：，则，故C错误；

对于D：定义域为，且，符合题意；

故选：D

11．设，，，则的大小关系为（    ）

A． B． C． D．

【答案】A

【分析】根据指数函数、对数函数的性质判断即可；

【详解】解：因为，，即，

，

所以；

故选：A

12．已知，则“”是“”的（    ）

A．充分不必要条件 B．必要不充分条件

C．充要条件 D．既不充分也不必要条件

【答案】A

【分析】判断条件间的推出关系，根据充分必要性的定义判断即可.

【详解】当：

若异号，即，显然成立；

若或，均有成立；

所以充分性成立；

当：若，，显然不成立，故必要性不成立.

所以“”是“”的充分不必要条件.

故选：A

13．已知幂函数上单调递增，则（    ）

A．0 B． C． D．

【答案】A

【分析】由题意可得且，从而可求出的值

【详解】因为幂函数上单调递增，

所以且，

解得，

故选：A

14．某几何体的三视图如图所示，则该几何体的体积是（    ）

A． B． C． D．

【答案】D

【分析】根据三视图得出原几何体是六棱柱，再由棱柱的体积公式计算体积即可求解.

【详解】由三视图可知：该几何体是六棱柱，

底面积，高，

所以几何体的体积为：，

故选：D.

15．如图所示，在平行四边形中，，沿将折起，使平面平面，连接，则在四面体的四个面中，互相垂直的平面的对数为（    ）

A．1 B．2 C．3 D．4

【答案】C

【分析】利用线面垂直得到平面平面，平面平面，平面平面，得到答案.

【详解】平面平面，平面平面，

，平面，故平面，平面，故平面平面；

，平面，故平面，平面，故平面平面；

综上所述：平面平面；平面平面；平面平面；

故选：C

16．已知正实数，且，则 的最小值是（    ）

A． B． C． D．

【答案】C

【分析】将变为，即可得，因此将变为，结合基本不等式即可求得答案.

【详解】因为正实数，，故，

所以，

故，

当且仅当时取得等号，

故选：C

17．下列函数中，在定义域内既是奇函数又单调递增的是（    ）

A． B．

C． D．

【答案】D

【分析】根据函数的奇偶性的定义，单调性的定义判断，从而可得答案．

【详解】对于A，因为，定义域为R，所以，所以是偶函数，所以不正确；

对于B，因为定义域为R ，，所以是奇函数，但在上是减函数，所以不正确；

对于C，因为的定义域为不关于原点对称，所以不具备奇偶性，所以不正确；

对于D，因为，定义域为R，，

是奇函数，设，则，

因为，所以，，

所以，即，是定义域为R的单调递增函数，所以正确.

故选：D．

18．已知函数，若函数只有两个零点，则实数的取值范围是（   ）

A． B． C．  D．

【答案】D

【分析】先求解为0时的值，可得只有两个零点，再根据分析可得无解，进而求得的取值范围即可.

【详解】由题意，即或.因为，易得无解.故只有两个零点.

当时，或，解得或有两个零点.故无解. 因为，，故，解得

故选：D

二、填空题（本大题共4小题，每空3分，共12分）

19．城区某道路上甲、乙、丙三处设有信号灯，汽车在这三处因遇绿灯而通行的概率分别为，，则汽车在这三处因遇红灯或黄灯而停车一次的概率为________．

【答案】

【分析】根据互斥事件概率求法即可得解.

【详解】∵设汽车分别在甲乙丙三处的通行为事件，停车为，

∴，，，

∵停车一次即为事件，

∴所求概率为：．

故答案为: .

20．已知，复数且 (为虚数单位) ，则复数的模为____．

【答案】

【分析】将代入中化简，再根据复数相等的条件可求出，从而可求出复数，进而可求得复数的模

【详解】因为，所以，

所以，

所以，解得，

所以

所以，

故答案为：

21．已知，函数在区间上有两个不同的零点，则的取值范围是________.

【答案】

【分析】由可得对称轴为，结合，，，可得

，，计算结合二次函数的性质即可求解.

【详解】的对称轴为，

因为函数在区间上有两个不同的零点，

所以，可得，

所以

，

因为，所以当，即，

综上所述：，

所以的取值范围是：，

故答案为：.

22．已知是平面向量，与是单位向量，且，若，则的最小值为_____________．

【答案】

【分析】把条件的二次方程分解成两个向量的积，得到这两个向量互相垂直，结合图形确定的最小值.

【详解】如下图所示，设

且

点B在以F为圆心，DE为直径的圆上

又

当点B为圆F和线段FA的交点的时候，最短

故答案为：

三、解答题（本大题共3小题，共34分）

23．已知函数，．

(1)求的值及的最小正周期；

(2)当时，求函数的零点所构成的集合．

【答案】(1)，最小正周期为;

(2)

【分析】（1）利用三角恒等变换化简函数的解析式，利用正弦函数的性质即可求解；

（2）令，可得或或，即可求解的值.

（1）解：因为 ，所以，最小正周期为 .

（2）令，则，因为，所以，所以或或，即或或，所以函数的零点所构成的集合为.

24．如图，在三棱锥中，，平面，点，分别为线段，的中点．

（1）求证：平面；

（2）设二面角的平面角为，若，，求的值．

【答案】（1）证明见解析；（2）.

【分析】（1）由平面得，即可结合得证；

（2）取的中点为，连接，，过用交于，连接，，可得即为二面角的平面角，由可求出.

【详解】（1）证明：∵平面，平面，∴，

又∵，，∴平面

（2）解：∵平面，∴，，

又平面，∴，，即，，互相垂直．

如图，取的中点为，连接，，

∵点，分别为线段，的中点，

∴，，，

∴，，平面，

且，，，

∴，

∴，∴是等边三角形，

过用交于，连接，，

∴，，

∴．

25．已知函数.

(1)当，且时，求的取值范围；

(2)是否存在正实数a，，使得函数在上的取值范围是.若存在，则求出a，b的值；若不存在，请说明理由.

【答案】(1)

(2)存在，，

【分析】（1）根据条件得到的关系，代入消去得到关于的函数，求其最值即可；

（2）假设存在满足条件的实数a，b，且，分a，，a，，，讨论，列方程组求解.

【详解】（1）因为，

所以在上为减函数，在上为增函数，

由且，可得且，

故.

令，则，函数在上单调递增，所以，

即的取值范围是.

（2）存在满足条件的实数a，b，理由如下：

假设存在满足条件的实数a，b，且.

①当a，时，在上单调递减，

则由，即，

解得ab=1，因为a，，故此时不存在符合条件的实数a，b.

②当a，时，在上单调递增.

则由，即，

所以a，b是方程得或，

所以，此时存在符合条件的实数，.

③当，时，由于，而，故此时不存在符合条件的实数a，b.

综上所述，存在符合条件的实数，.