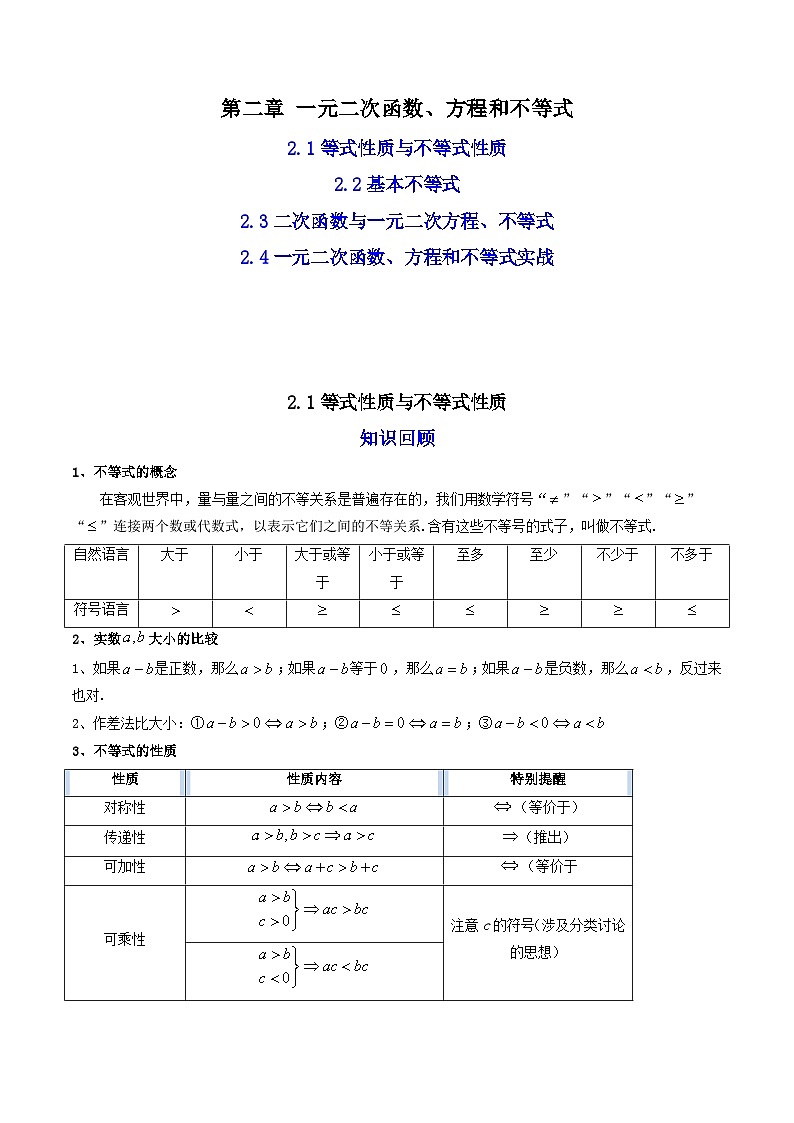
02第二章 一元二次函数、方程和不等式——2023年高中数学学业水平考试专项精讲+测试（人教A版2019，新教材地区）

第二章 一元二次函数、方程和不等式

2.1等式性质与不等式性质

2.2基本不等式

2.3二次函数与一元二次方程、不等式

2.4一元二次函数、方程和不等式实战

2.1等式性质与不等式性质

知识回顾

1、不等式的概念

在客观世界中，量与量之间的不等关系是普遍存在的，我们用数学符号“”“”“”“”“”连接两个数或代数式，以表示它们之间的不等关系.含有这些不等号的式子，叫做不等式.

2、实数大小的比较

1、如果是正数，那么；如果等于，那么；如果是负数，那么，反过来也对.

2、作差法比大小：①；②；③

3、不等式的性质

高频考点

1．（2022·贵州·高二学业考试）已知，则下列不等关系中一定成立的是（    ）

A． B． C． D．

2．（2022·北京·高三学业考试）已知a，b是实数，且，则（    ）

A． B． C． D．

3．（2022·湖南娄底·高二学业考试）已知，bR，且＜b，则下列不等式一定成立的是（    ）

A．+3<b+3 B．5>b5 C．2>2b D．

4．（2022·宁夏·青铜峡市宁朔中学高二学业考试）若，则下列关系一定成立的是（    ）

A． B．

C． D．

5．（2022·浙江·诸暨市教育研究中心高二学业考试）已知，，则的范围是（   ）

A． B． C． D．

6．（2022·浙江·台州市书生中学高二学业考试）（1）已知,求的取值范围；

（2）已知实数满足求的取值范围.

2.2基本不等式

知识回顾

1、基本不等式（一正，二定，三相等，特别注意“一正”，“三相等”这两类陷阱）

①如果，，，当且仅当时，等号成立．

②其中叫做正数，的几何平均数；叫做正数，的算数平均数．

2、两个重要的不等式

①（）当且仅当时，等号成立．

②（）当且仅当时，等号成立．

3、利用基本不等式求最值

①已知，是正数，如果积等于定值，那么当且仅当时，和有最小值；

②已知，是正数，如果和等于定值，那么当且仅当时，积有最大值；

高频考点

1．（2022·湖南·怀化市辰溪博雅实验学校高二学业考试）已知，则的最小值是（    ）

A． B． C． D．

2．（2022·浙江·诸暨市教育研究中心高二学业考试）设x，y为正数，则的最小值为（    ）

A．6 B．9 C．12 D．15

3．（2022·湖北·高二学业考试）已知正实数、满足，则的取值可能为（    ）

A． B． C． D．

4．（2022·浙江·太湖高级中学高二学业考试）已知且，则的最小值为（    ）

A．3+ B．4 C．2 D．6

5．（2022·浙江·诸暨市教育研究中心高二学业考试）已知正实数，且，则 的最小值是（    ）

A． B． C． D．

6．（多选）（2022·浙江·诸暨市教育研究中心高二学业考试）已知实数，，，则的值可能是（    ）

A．7 B．8 C．9 D．10

7．（多选）（2022·浙江·慈溪市三山高级中学高二学业考试）已知正实数满足，则（    ）

A．

B．的最小值为

C．的最小值为9

D．的最小值为

8．（2022·天津河东·高二学业考试）若正数a，b满足，则的最小值为___________.

9．（2022·天津南开·高二学业考试）若，则的最大值是______．

10．（2022·宁夏·青铜峡市宁朔中学高二学业考试）函数的值域为__________．

2.3二次函数与一元二次方程、不等式

知识回顾

1、二次函数

（1）形式：形如的函数叫做二次函数.

（2）特点：

①函数的图象与轴交点的横坐标是方程的实根.

②当且()时，恒有()；当且()时，恒有().

2、一元二次不等式

只含有一个未知数，并且未知数的最高次数是2的不等式，称为一元二次不等式.

3.或型不等式的解集

4、一元二次不等式与相应的二次函数及一元二次方程的关系

高频考点

1．（2022·贵州·高二学业考试）不等式的解集是（    ）

A． B． C． D．

2．（2022·湖南·怀化市辰溪博雅实验学校高二学业考试）的解集为（    ）

A． B．或 C． D．

3．（2022·广西·高二学业考试）不等式的解集为（     ）

A．R B． C． D．

4．（2022·浙江·高三学业考试）不等式的解集为（    ）

A． B．

C． D．或

5．（2022·宁夏·青铜峡市宁朔中学高二学业考试）不等式的解集为__________________..

6．（2022·宁夏·青铜峡市宁朔中学高二学业考试）已知不等式，若不等式的解集为或，求的值.

7．（2022·天津红桥·高二学业考试）已知函数，其中，.

(1)若，求实数的值；

(2)若时，求不等式的解集；

(3)求不等式的解集.

2.4一元二次函数、方程和不等式实战

一、单选题

1．若，则下列正确的是（    ）

A． B． C． D．

2．下列结论正确的是（    ）

A．若，则 B．若，，则

C．若，则 D．若，则

3．不等式的解集是（    ）

A． B．

C． D．

4．已知，则的最小值是（    ）

A．1 B．2 C．3 D．4

5．已知，那么函数有（    ）

A．最大值2 B．最小值2 C．最小值4 D．最大值4

6．不等式的解集为（   ）

A． B． C． D．

7．已知正数，满足，则的最小值为（     ）

A． B．2 C． D．6

8．若不等式对任意实数x均成立，则实数a的取值范围是（    ）

A． B． C． D．

二、多选题

9．若a，b，c∈R，且a>b，则下列不等式一定成立的是（    ）

A．a+c>b+c B．ac2≥bc2

C． D．(a+b)(a-b)>0

10．已知正实数满足，则（    ）

A．

B．的最小值为

C．的最小值为9

D．的最小值为

三、填空题

11．不等式的解集是______.

12．已知，，，则的最小值为__________．

13．已知函数，在区间上不单调，则实数的取值范围是___________．

14．已知△ABC三内角A，B，C所对的边分别是a，b，c，D是线段BC上任意一点，ADBC，且AD＝BC，则的取值范围是_________.

四、解答题

15．已知函数，其中 .

（1）若，求实数的值；

（2）若时，求不等式的解集；

（3）求不等式的解集.

16．近年来，某西部乡村农产品加工合作社每年消耗电费24万元.为了节能环保，决定修建一个可使用16年的沼气发电池，并入该合作社的电网.修建沼气发电池的费用（单位：万元）与沼气发电池的容积（单位：米3）成正比，比例系数为0.12.为了保证正常用电，修建后采用沼气能和电能互补的供电模式用电.设在此模式下，修建后该合作社每年消耗的电费（单位：万元）与修建的沼气发电池的容积（单位：米3）之间的函数关系为（，k为常数）.记该合作社修建此沼气发电池的费用与16年所消耗的电费之和为（单位：万元）.

（1）解释的实际意义，并写出关于的函数关系；

（2）该合作社应修建多大容积的沼气发电池，可使最小，并求出最小值.

（3）要使不超过140万元，求的取值范围.