2022-2023学年山东省临沂市临沭县七年级（下）期中数学试卷（含解析）

这是一份2022-2023学年山东省临沂市临沭县七年级（下）期中数学试卷（含解析），共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
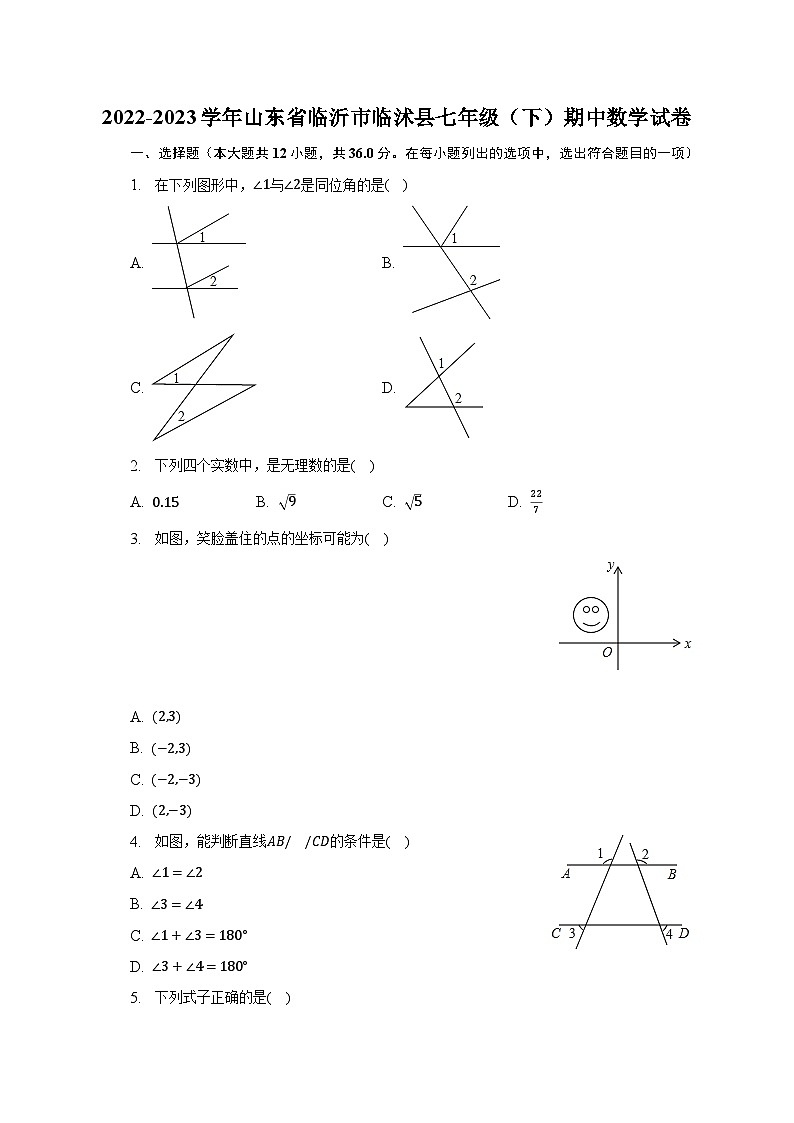
2022-2023学年山东省临沂市临沭县七年级（下）期中数学试卷一、选择题（本大题共12小题，共36.0分。在每小题列出的选项中，选出符合题目的一项）1.  在下列图形中，与是同位角的是(    )A.  B.
C.  D. 2.  下列四个实数中，是无理数的是(    )A.  B.  C.  D. 3.  如图，笑脸盖住的点的坐标可能为(    )
 
 A.
B.
C.
D. 4.  如图，能判断直线的条件是(    )A.
B.
C.
D. 5.  下列式子正确的是(    )A.  B.  C.  D. 6.  下列说法正确的是(    )A. 的平方根是 B. 是的一个平方根
C. 没有立方根 D. 立方根等于它本身的数是，7.  以下各点中，距离轴个单位长度的点是(    )A.  B.  C.  D. 8.  下列命题：
内错角相等；
两个锐角的和是钝角；
，，是同一平面内的三条直线，若，，则；
，，是同一平面内的三条直线，若，，则；
其中真命题的个数是(    )A. 个 B. 个 C. 个 D. 个9.  将一张长方形纸条沿折叠，点，分别落在，位置上，与的交点为若，则的度数为(    )A.
B.
C.
D. 10.  如图的围棋盘放置在某个平面直角坐标系内，白棋的坐标为，白棋的坐标为，那么黑棋的坐标应该是(    )A.
B.
C.
D. 11.  如图摆放的一副学生用直角三角板，，，与相交于点，当时，的度数是(    )

 A.  B.  C.  D. 12.  对于整数，定义为不大于的最大整数，例如：，，对进行如下操作：，即对进行次操作后变为，对整数进行次操作后变为，则的最大值为(    )A.  B.  C.  D. 二、填空题（本大题共4小题，共16.0分）13.  的绝对值是______ ，是______ 的算术平方根．14.  如图，请你添加一个条件使得，所添的条件是______．
 15.  大自然是美的设计师，即使是一片小小的树叶，也蕴含着“美学”，如图．，这个比值介于整数和之间，则的值是______．
 16.  平面直角坐标系中，点，，，若轴，则线段取最小值时的坐标为______．三、解答题（本大题共7小题，共68.0分。解答应写出文字说明，证明过程或演算步骤）17.  本小题分
计算：
；
．18.  本小题分
求下列各式中的值．
；
．19.  本小题分
如图，直线，相交于点，，垂足为．
直接写出图中的对顶角为______，的邻补角为______；
若：：，求的度数．
20.  本小题分
填空完成推理过程：
如图，，的平分线交于点，交的延长线于点，，求证：．
请将下面的证明过程补充完整：
证明：已知，
______ ．
平分，
______ ．
______
______ ，
______ ．
______
______
 
21.  本小题分
如图，在平面直角坐标系中，已知，，，．
在图中描出上述各点；
有一直线通过点且与轴垂直，则也会通过点______填“”“”“”或“”；
连接，将线段平移得到，若点，在图中画出，并写出点的坐标；
若，求三角形的面积．
22.  本小题分
如图，已知，．
请你判断与的位置关系，并说明理由；
若平分，于，，试求的度数．
 
 
 23.  本小题分
课题学习：平行线的“等角转化”功能．

阅读理解：如图，已知点是外一点，连接、，求的度数阅读并补充下面推理过程．
解：过点作，        ，        ，，．
解题反思：从上面的推理过程中，我们发现平行线具有“等角转化”的功能，将、、“凑”在一起，得出角之间的关系，使问题得以解决．
方法运用：如图，已知，求的度数；
深化拓展：已知，点在点的右侧，，平分，平分，，所在的直线交于点，点在直线与之间．
如图，点在点的左侧，若，求的度数．
如图，点在点的右侧，且，若，求度数用含的代数式表示

答案和解析 1.【答案】 【解析】解：根据同位角的定义可知答案是D．
故选：．
同位角就是：两个角都在截线的同旁，又分别处在被截的两条直线同侧的位置的角．
解答此类题确定三线八角是关键，可直接从截线入手．对平面几何中概念的理解，一定要紧扣概念中的关键词语，要做到对它们正确理解，对不同的几何语言的表达要注意理解它们所包含的意义．
 2.【答案】 【解析】解：是有限小数，属于有理数，故本选项不合题意；
B.，是整数，属于有理数，故本选项不合题意；
C.是无理数，故本选项符合题意；
D.是分数，属于有理数，故本选项不合题意；
故选：．
无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．
此题主要考查了无理数的定义，其中初中范围内学习的无理数有：，等；开方开不尽的数；以及像相邻两个之间依次多一个，等有这样规律的数．
 3.【答案】 【解析】【分析】
此题主要考查了点的坐标，得出笑脸的横纵坐标符号是解题关键．
根据图形得出笑脸的位置，进而得出答案．
【解答】
解：由图形可得：笑脸在第二象限，即横坐标符号为负，纵坐标符号为正，则笑脸盖住的点的坐标可能为．
故选：．  4.【答案】 【解析】解：，，
，
，
故选：．

根据邻补角互补和条件，可得，再根据同位角相等，两直线平行可得结论．
此题主要考查了平行线的判定，关键是掌握：同位角相等，两直线平行．
 5.【答案】 【解析】解：，故选项A不正确；
，故选项B不正确；
，故选项C不正确；
，故选项D正确．
故选：．
根据二次根式的性质进行化简，然后逐一判断即可．
此题考查的是二次根式的性质，掌握其性质是解决此题关键．
 6.【答案】 【解析】解：的平方根是和，
选项A不符合题意；
的平方根是和，
是的一个平方根，
选项B符合题意；
的立方根是，
选项C不符合题意；
立方根等于它本身的数是，，
选项D不符合题意，
故选：．
运用平方根和立方根的知识进行辨别、求解．
此题考查了平方根和立方根知识的运用能力，关键是能准确理解并运用以上知识．
 7.【答案】 【解析】【分析】
本题主要考查了坐标与图形性质，掌握到轴的距离与纵坐标有关，到轴的距离与横坐标有关是解题关键．
根据距离轴个单位长度，得纵坐标的绝对值是．
【解答】
解：距离轴个单位长度，
，
，
故选：．  8.【答案】 【解析】【分析】
本题主要考查命题与定理知识，熟练掌握平行线的判定及性质、平行公理等知识是解答此题的关键．
根据平行线的判定及性质、平行公理等知识逐项判定即可．
【解答】
解：两直线平行、内错角相等，故为假命题；
两个锐角的和不一定是钝角，例如和，这两个锐角之和就不是钝角，故为假命题；
，，是同一平面内的三条直线，若，，则，正确，故为真命题；
，，是同一平面内的三条直线，若，，则，故为假命题；
真命题为，
故选：．  9.【答案】 【解析】解：，
，
由折叠的性质可知，，
．
故选：．
根据平行线的性质求出的度数，根据折叠的性质解答即可．
本题考查的是平行线的性质以及折叠的性质，根据已知得出是解题关键．
 10.【答案】 【解析】解：如图所示：黑棋的坐标为，
故选：．
首先建立坐标系，然后再确定黑棋的坐标即可．
此题主要考查了坐标确定位置，关键是正确建立坐标系．
 11.【答案】 【解析】【分析】
本题主要考查了平行线的性质，其中平行线的性质为：两直线平行，内错角相等；其中正确作出辅助线是解本题的关键．
过点作，则有，，又因为和都是特殊直角三角形，，，可以得到，，由即可得出答案．
【解答】
解：过点作，

，
，
，，
在和中，，，
，，
，，
，
故的度数是，
故选D．  12.【答案】 【解析】解：，，，
对只需进行次操作后变为，
，，，
只需进行次操作后变为的所有正整数中，最大的是，
的最大值为．
故选：．
由的定义为不大于的最大整数，进行次操作后变为，进行次操作后变为，据此可得出的最大值．
本题本题考查了估算无理数的大小，的定义，熟知估算无理数大小的方法是解决此题的关键．
 13.【答案】   【解析】解：的绝对值是，
的算术平方根是．
故答案为：，．
分别根据绝对值以及算术平方根的定义即可求解．
此题主要考查了绝对值的定义、算术平方根的定义，其中利用了一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；的绝对值是．
 14.【答案】答案不唯一 【解析】解：根据同位角相等，两条直线平行，可以添加；
根据内错角相等，两条直线平行，可以添加；
根据同旁内角互补，两条直线平行，可以添加，
故答案为：或或答案不唯一．
根据平行线的判定方法进行添加．
此题考查了平行线的判定，为开放性试题，答案不唯一，熟悉平行线的判定方法是解题的关键．
 15.【答案】 【解析】解：，
，

，为整数，
．
故答案为．
先估计，再求值．
本题考查无理数的估计，正确判断的范围是求解本题的关键．
 16.【答案】 【解析】解：如图所示：

由垂线段最短可知：当时，有最小值．
点的坐标为，线段的最小值为．
故答案是：．
由垂线段最短可知点时，有最小值，从而可确定点的坐标．
本题主要考查坐标与图形性质，掌握垂线段的性质是解题的关键．
 17.【答案】解：

；


． 【解析】本题涉及负整数指数幂、绝对值、二次根式和三次根式的化简，乘方个知识点．在计算时，需要针对每个知识点分别进行计算，然后根据实数的运算法则求得计算结果．
先算乘法，再算加减法．
本题主要考查了实数的综合运算能力，是各地中考题中常见的计算题型．解决此类题目的关键是熟练掌握负整数指数幂、二次根式和三次根式、乘方、绝对值等知识点的运算．
 18.【答案】解：化系数为，得，
开平方，得或；
移项，得，
系数化为，得，
开立方，得，
解得． 【解析】运用平方根知识进行求解；
通过移项、化系数为、开立方进行求解．
此题考查了运用平方根和立方根解方程的能力，关键是能准确理解并运用以上知识进行正确地计算．
 19.【答案】；，
 【解析】解：的对顶角为，的邻补角为，，
故答案为：；，．
，
，
，
，
：：，
，
 
直接利用对顶角以及邻补角的定义得出答案；
直接利用垂直的定义得出答案．
此题主要考查了垂线以及角平分线定义、对顶角等知识，正确得出的度数是解题关键．
 20.【答案】    等量代换  已知    两直线平行，同位角相等  等量代换 【解析】证明：已知，
，
平分，
．
等量代换．
已知，
．
两直线平行，同位角相等．
等量代换．
答案为：；；等量代换；已知；；两直线平行，同位角相等；等量代换．
根据题目中的每一步推理过程，结合图形填写平行线的判定和性质即可．
此题主要考查了平行线的判定和性质，解答此题的关键是准确识图，熟练掌握平行线的判定及性质：两直线平行同位角相等，两直线平行内错角相等，两直线平行同旁内角互补．
 21.【答案】 【解析】解：如图所示，点，，，即为所求；

如图，直线即为所求，则会通过点；
故答案为：；
如图，即为所求，的坐标为；
，
三角形的面积．
根据平面直角坐标系即可描出各点，，，；
根据直线通过点且与轴垂直，进而可以解决问题；
根据平移的性质即可将线段平移得到，进而可以写出点的坐标；
根据，即可求三角形的面积．
本题考查了作图平移变换，解决本题的关键是掌握平移的性质．
 22.【答案】解：，
理由是：，
，
，
又，
，
．
平分，
，
，
，，
，
． 【解析】根据平行线的判定推出，推出，求出，根据平行线的判定推出即可；
求出的度数，求出，，代入求出即可．
本题考查了平行线的性质和判定，角平分线定义的应用，注意：平行线的性质有：两直线平行，同位角相等，两直线平行，内错角相等，两直线平行，同旁内角互补．
 23.【答案】   【解析】解：，
，两直线平行，内错角相等；
故答案为：；；
过作，
，
，
，
，
，
，
；
过作，
，
，
，
平分，
，
，
平分，
，
，
，
；
过作，
，
，
，
平分，，
，
，
，
，
．

由“两直线平行，内错角相等”可得结果；
过作，利用“两直线平行，同旁内角互补”可以求得结果；
过作，利用角平分线的概念求得，，再利用“两直线平行，内错角相等”导角即可；过作，利用角平分线的概念求得，，再利用平行线的性质求角即可．
本题考查了平行线的性质、平行线的传递性以及角平分线的概念，作出辅助线构造平行线导角是解决本题的关键．