高中数学人教A版 (2019)选择性必修第一册第三章圆锥曲线的方程3.1 椭圆学案设计

展开

这是一份高中数学人教A版 (2019)选择性必修第一册第三章圆锥曲线的方程3.1 椭圆学案设计，共21页。

3.1.2　椭圆的简单几何性质

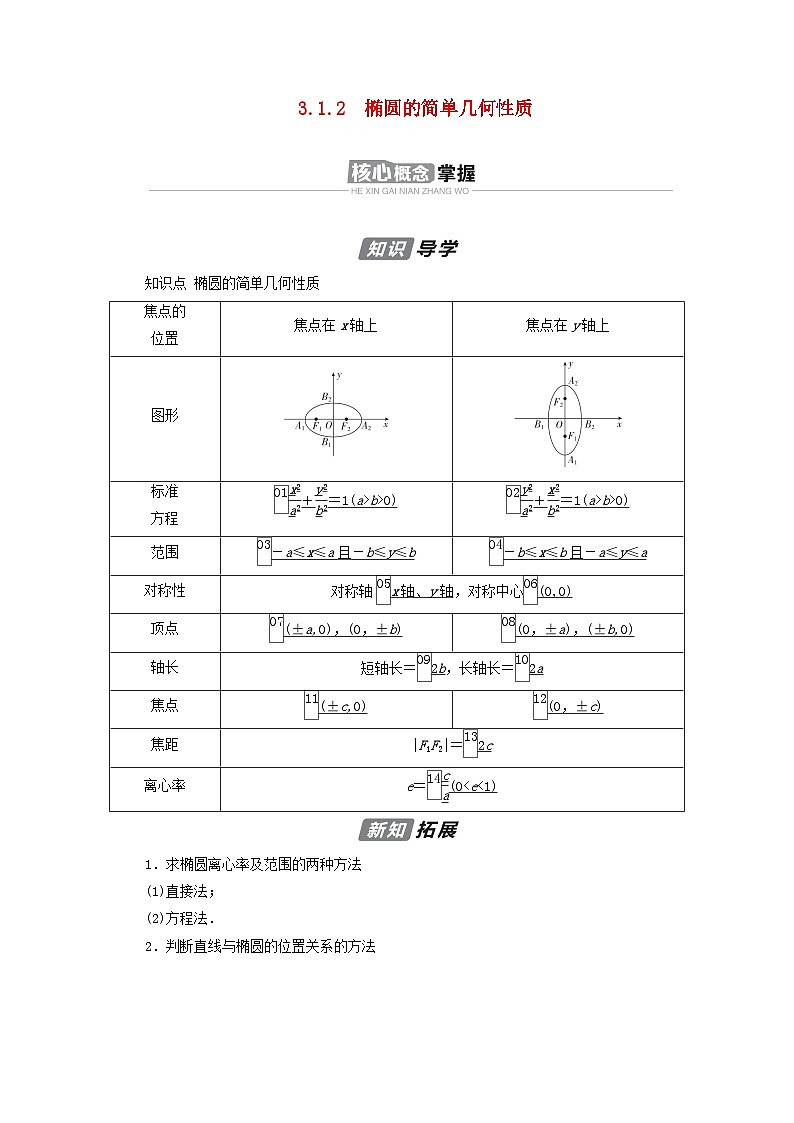
知识点椭圆的简单几何性质
焦点的
位置
焦点在x轴上
焦点在y轴上
图形

标准
方程
＋＝1(a>b>0)
＋＝1(a>b>0)
范围
－a≤x≤a且－b≤y≤b
－b≤x≤b且－a≤y≤a
对称性
对称轴x轴、y轴，对称中心(0,0)
顶点
(±a,0)，(0，±b)
(0，±a)，(±b,0)
轴长
短轴长＝2b，长轴长＝2a
焦点
(±c,0)
(0，±c)
焦距
|F1F2|＝2c
离心率
e＝(0
1．求椭圆离心率及范围的两种方法
(1)直接法；
(2)方程法．
2．判断直线与椭圆的位置关系的方法

3．求弦长的两种方法
(1)求出弦两端点的坐标，然后利用两点间的距离公式求解；
(2)结合根与系数的关系，利用弦长公式
l＝
或l＝求解．
4．两个特殊结论
(1)如图，过椭圆的一个焦点且与长轴垂直的弦|AB|＝，称为通径；

(2)椭圆上的点到一焦点的最大距离为a＋c，最小距离为a－c.
5．解决椭圆中点弦问题的三种方法
(1)根与系数的关系法；
(2)点差法；
(3)共线法．

1．判一判(正确的打“√”，错误的打“×”)
(1)椭圆＋＝1(a>b>0)的长轴长等于a.(　　)
(2)椭圆上的点到焦点的距离的最小值为a－c.(　　)
(3)椭圆的离心率e越小，椭圆越圆．(　　)
答案　(1)×　(2)√　(3)√
2．做一做
(1)椭圆25x2＋9y2＝225的长轴长、短轴长、离心率依次是(　　)
A．5,3， B．10,6，
C．5,3， D．10,6，
(2)椭圆x2＋9y2＝36的短轴的端点为________.
(3)设P(m，n)是椭圆＋＝1上任意一点，则m的取值范围是________.
答案　(1)B　(2)(0,2)，(0，－2)　(3)[－5,5]

题型一椭圆的简单几何性质
例1　已知椭圆x2＋(m＋3)y2＝m(m>0)的离心率e＝，求m的值及椭圆的长轴长、短轴长、焦点坐标、顶点坐标．
[解]　椭圆方程可化为＋＝1.
∵m－＝>0，∴m>，
∴椭圆焦点在x轴上，即
a2＝m，b2＝，c＝＝ .
由e＝得＝，
∴m＝1.
∴椭圆的标准方程为x2＋＝1.
∴a＝1，b＝，c＝.
∴椭圆的长轴长为2；短轴长为1；两焦点坐标分别为F1，F2；四个顶点分别为A1(－1,0)，A2(1,0)，B1，B2.

1．用标准方程研究几何性质的步骤
(1)将椭圆方程化为标准形式．
(2)确定焦点位置．
(3)求出a，b，c.
(4)写出椭圆的几何性质．
2．根据椭圆的几何性质求标准方程
此类问题通常采用待定系数法，其步骤仍然是“先定型，后计算”，即首先确定焦点位置，其次根据已知条件构造关于参数的关系式，利用方程(组)求得参数．
[跟踪训练1]　求适合下列条件的椭圆的标准方程．
(1)长轴长是短轴长的5倍，且过点A(5,0)；
(2)离心率e＝，焦距为12.
解　(1)若椭圆焦点在x轴上，设其标准方程为＋＝1(a>b>0)，
由题意得解得
故所求椭圆的标准方程为＋y2＝1；
若焦点在y轴上，设其标准方程为＋＝1(a>b>0)，
由题意得解得
故所求椭圆的标准方程为＋＝1.
综上所述，所求椭圆的标准方程为＋y2＝1或＋＝1.
(2)由e＝＝，2c＝12，得a＝10，c＝6，
∴b2＝a2－c2＝64.
当焦点在x轴上时，所求椭圆的标准方程为＋＝1；
当焦点在y轴上时，所求椭圆的标准方程为＋＝1.
综上所述，所求椭圆的标准方程为＋＝1或＋＝1.
题型二椭圆的离心率问题
例2　直线l经过椭圆的一个顶点和一个焦点，若椭圆中心到l的距离为其短轴长的，则该椭圆的离心率为(　　)
A. B．
C． D．
[解析]　解法一：不妨设直线l过椭圆的上顶点(0，b)和左焦点(－c，0)，b>0，c>0，则直线l的方程为bx－cy＋bc＝0，由已知得＝×2b，解得b2＝3c2，又b2＝a2－c2，所以＝，即e2＝，所以 e＝.
解法二：如图，由题意得在椭圆中，|OF|＝c，|OB|＝b，|OD|＝×2b＝b，|BF|＝a.

在Rt△OFB中，|OF|×|OB|＝|BF|×|OD|，即c×b＝a×b，解得＝，所以椭圆的离心率e＝.故选B.
[答案]　B

求椭圆离心率及范围的两种方法
(1)直接法：若已知a，c可直接利用e＝求解．若已知a，b或b，c可借助于a2＝b2＋c2求出c或a，再代入公式e＝求解．
(2)方程法：若a，c的值不可求，则可根据条件建立a，b，c的关系式，借助于a2＝b2＋c2，转化为关于a，c的齐次方程或不等式，再将方程或不等式两边同除以a的最高次幂，得到关于e的方程或不等式，即可求得e的值或范围．
[跟踪训练2]　(1)已知F1(－c,0)，F2(c,0)为椭圆＋＝1的两个焦点，P为椭圆上一点且·＝c2，则此椭圆离心率的取值范围是(　　)
A. B．
C. D．
答案　C
解析　设P(m，n)，·＝c2＝(－c－m，－n)·(c－m，－n)＝m2－c2＋n2,2c2－m2＝n2，①
把P(m，n)代入椭圆＋＝1得b2m2＋a2n2＝a2b2，②
把①代入②得m2＝≥0，∴a2b2≤2a2c2，
∴b2≤2c2，∴a2≤3c2，∴e＝≥.
又m2＝≤a2，∴a2≥2c2，∴e＝≤.
综上可知，此椭圆离心率的取值范围是.故选C.
(2)已知F1为椭圆的左焦点，A，B分别为椭圆的右顶点和上顶点，P为椭圆上的点，当PF1⊥F1A，PO∥AB(O为椭圆中心)时，求椭圆的离心率．

解　解法一：由已知可设椭圆的方程为＋＝1(a>b>0)，
c2＝a2－b2，F1(－c,0)，∵PF1⊥F1A，
∴P，即P，
∵AB∥PO，∴kAB＝kOP，即－＝－，
∴b＝c，∴a2＝2c2，∴e＝＝.
解法二：由解法一知P，又△PF1O∽△BOA，
∴＝，∴＝，即b＝c，
∴a2＝2c2，∴e＝＝.
题型三直线与椭圆的位置关系
例3　已知椭圆E：＋＝1(a>b>0)的两个焦点与短轴的一个端点是直角三角形的三个顶点，直线l：y＝－x＋3与椭圆E有且只有一个公共点T.
(1)求椭圆E的方程及点T的坐标；
(2)设O是坐标原点，直线l′平行于OT，与椭圆E交于不同的两点A，B，且与直线l交于点P.证明：存在常数λ，使得|PT|2＝λ|PA|·|PB|，并求λ的值．
[解]　(1)由已知得a＝b，则椭圆E的方程为＋＝1.
由方程组得3x2－12x＋(18－2b2)＝0.①
方程①的判别式为Δ＝24(b2－3)，由Δ＝0，得b2＝3，
此时方程①的解为x＝2，所以椭圆E的方程为＋＝1，点T的坐标为(2,1)．
(2)由已知可设直线l′的方程为y＝x＋m(m≠0)，
由方程组可得
所以P点的坐标为，|PT|2＝m2.
设点A，B的坐标分别为A(x1，y1)，B(x2，y2)．
由方程组
可得3x2＋4mx＋(4m2－12)＝0.②
方程②的判别式为Δ＝16(9－2m2)，
由Δ>0，解得－由②得x1＋x2＝－，x1x2＝.
所以|PA|＝
＝，
同理|PB|＝.
所以|PA|·|PB|
＝
＝
＝
＝m2.
故存在常数λ＝，使得|PT|2＝λ|PA|·|PB|.

1．解决直线与椭圆的位置关系问题经常利用设而不求方法的解题步骤
(1)设直线与椭圆的交点为A(x1，y1)，B(x2，y2)．
(2)联立直线与椭圆的方程．
(3)消元得到关于x或y的一元二次方程．
(4)利用根与系数的关系设而不求．
(5)把题干中的条件转化为x1＋x2，x1x2或y1＋y2，y1y2，进而求解．
2．直线与椭圆相交弦长的有关问题
(1)当弦的两端点的坐标易求时，可直接求出交点坐标，再用两点间距离公式求弦长．
(2)当弦的两端点的坐标不易求时，可用弦长公式．
(3)如果直线方程涉及斜率，要注意斜率不存在的情况．
[跟踪训练3]　(1)在椭圆＋＝1上求一点P，使它到直线l：3x－2y－16＝0的距离最短，并求出最短距离．
解　设与椭圆相切并与l平行的直线方程为y＝x＋m，代入＋＝1，

并整理得4x2＋3mx＋m2－7＝0，
Δ＝9m2－16(m2－7)＝0⇒m2＝16⇒m＝±4，
故两切线方程为y＝x＋4和y＝x－4，显然y＝x－4距l最近，所以d＝＝＝，切点为P.
(2)已知椭圆4x2＋y2＝1及直线y＝x＋m.
①当直线和椭圆有公共点时，求实数m的取值范围；
②求被椭圆截得的最长弦所在的直线方程．
解　①由得5x2＋2mx＋m2－1＝0，
因为直线与椭圆有公共点，
所以Δ＝4m2－20(m2－1)≥0，
解得－≤m≤.
②设直线与椭圆交于A(x1，y1)，B(x2，y2)两点，
由①知，5x2＋2mx＋m2－1＝0，
所以x1＋x2＝－，x1x2＝(m2－1)，
所以|AB|＝＝
＝＝
＝ .
所以当m＝0时，|AB|最大，此时直线方程为y＝x.
题型四椭圆的中点弦问题
例4　已知椭圆＋＝1，过点P(2,1)作一弦，使弦在这点被平分，求此弦所在直线的方程．
[解]　解法一：如图，易知直线斜率存在，设所求直线的方程为y－1＝k(x－2)，

代入椭圆方程并整理，得 (4k2＋1)x2－8(2k2－k)x＋4(2k－1)2－16＝0，(*)
又设直线与椭圆的交点为A(x1，y1)，B(x2，y2)，
则x1，x2是(*)方程的两个根，
∴x1＋x2＝.
∵P为弦AB的中点，∴2＝＝，
解得k＝－，
∴所求直线的方程为x＋2y－4＝0.
解法二：设直线与椭圆交点为A(x1，y1)，B(x2，y2)，
∵P为弦AB的中点，
∴x1＋x2＝4，y1＋y2＝2.
又∵A，B在椭圆上，∴x＋4y＝16，x＋4y＝16.
两式相减，得(x－x)＋4(y－y)＝0，
即(x1＋x2)(x1－x2)＋4(y1＋y2)(y1－y2)＝0.
∴＝＝－，即kAB＝－.
∴所求直线方程为y－1＝－(x－2)．
即x＋2y－4＝0.
解法三：设所求直线与椭圆的一交点为A(x，y)，
另一交点为B(4－x，2－y)，∵A，B在椭圆上，
∴x2＋4y2＝16，①
(4－x)2＋4(2－y)2＝16.②
①－②得x＋2y－4＝0，则A，B在直线x＋2y－4＝0上，
而过A，B的直线只有一条，
∴所求直线的方程为x＋2y－4＝0.

解决椭圆中点弦问题的三种方法
(1)根与系数的关系法：联立直线方程和椭圆方程构成方程组，消去一个未知数，利用一元二次方程根与系数的关系以及中点坐标公式解决．
(2)点差法：利用端点在曲线上，坐标满足方程，将端点坐标分别代入椭圆方程，然后作差，构造出中点坐标和斜率的关系．
(3)共线法：利用中点坐标公式，如果弦的中点为P(x0，y0)，设其一交点为A(x，y)，则另一交点为B(2x0－x,2y0－y)，
则
两式作差即得所求直线方程．
这三种方法中又以点差法最为常用，点差法中体现的设而不求思想还可以用于解决对称问题，因为这类问题也与弦中点和斜率有关．
与弦中点有关的问题有平行弦的中点轨迹、过定点且被定点平分的弦所在的直线方程等．这类问题的解决，从不同的角度体现了判别式、根与系数的关系、点差法、椭圆的性质、线段的垂直平分线的性质等知识在直线与椭圆的位置关系中的作用，解法多、方法活．
[跟踪训练4]　已知椭圆E：＋＝1(a>b>0)的右焦点为F(3,0)，过点F的直线交E于A，B两点．若AB的中点坐标为(1，－1)，则E的方程为(　　)
A.＋＝1 B．＋＝1
C.＋＝1 D．＋＝1
答案　D
解析　因为直线AB过点F(3,0)和点(1，－1)，所以直线AB的方程为y＝(x－3)，代入椭圆方程＋＝1消去y，得x2－a2x＋a2－a2b2＝0，所以AB的中点的横坐标为＝1，即a2＝2b2，又a2＝b2＋c2，所以b＝c＝3，选D.
题型五椭圆中的最值(或范围)问题
例5　已知椭圆E：＋＝1，点P(x，y)是椭圆上一点．
(1)求x2＋y2的最值；
(2)若四边形ABCD内接于椭圆E，点A的横坐标为5，点C的纵坐标为4，求四边形面积的最大值．
[解]　(1)解法一：由＋＝1，得y2＝16，
∴x2＋y2＝x2＋16＝16＋.
∵x∈[－5,5]，∴16≤x2＋y2≤25，
∴x2＋y2的最大值为25，最小值为16.
解法二：令θ∈[0,2π]，
得x2＋y2＝25cos2θ＋16sin2θ＝16＋9cos2θ.
又cos2θ∈[0,1]，∴x2＋y2的最大值为25，最小值为16.
(2)如图所示，易知A(5,0)，C(0，4)，不妨设B(5cosθ，4sinθ)在椭圆上且位于第一象限，则0<θ<.

又直线AC的方程为＋＝1，即4x＋5y－20＝0.
∴点B到直线AC的距离为d1＝
＝≤.
同理可得，点D到直线AC的距离为d2≤.
∴四边形ABCD的最大面积为S＝|AC|(d1＋d2)＝20.

1．解决椭圆＋＝1(a>b>0)中的范围问题常用的关系
(1)－a≤x≤a，－b≤y≤b；
(2)离心率0 (3)一元二次方程有解，则判别式Δ≥0.
2．解决与椭圆有关的最值问题常用的几种方法
(1)利用定义转化为几何问题处理；
(2)利用三角替代(换元法)转化为三角函数的最值问题处理；
(3)利用数与形的结合，挖掘数学表达式的几何特征，进而求解；
(4)利用函数最值的研究方法，将其转化为函数的最值问题来处理，此时，应注意椭圆中x，y的取值范围，常常是化为闭区间上的二次函数的最值来求解．
[跟踪训练5]　已知椭圆C：＋＝1(a>b>0)的左、右焦点分别为F1，F2，左顶点为A，离心率为，点B是椭圆C上的动点，△ABF1的面积的最大值为.
(1)求椭圆C的方程；
(2)设经过点F1的直线l与椭圆C相交于不同的两点M，N，线段MN的中垂线为l′，若直线l′与直线l相交于点P，与直线x＝2相交于点Q，求的最小值．
解　(1)由已知，有＝，即a2＝2c2.
∵a2＝b2＋c2，∴b＝c.
设B点的纵坐标为y0(y0≠0)，
则S△ABF1＝(a－c)·|y0|≤(a－c)b＝，
即(b－b)b＝－1.
∴b＝1，a＝.
∴椭圆C的方程为＋y2＝1.
(2)由题意知直线l的斜率不为0，故设直线l：x＝my－1.
设M(x1，y1)，N(x2，y2)，P(xP，yP)，Q(2，yQ)．
联立消去x，得
(m2＋2)y2－2my－1＝0，此时Δ＝8(m2＋1)>0，
∴y1＋y2＝，y1y2＝－.
由弦长公式，得
|MN|＝ ·|y1－y2|＝·，
整理得|MN|＝2·.
又yP＝＝，
∴xP＝myP－1＝ .
∴|PQ|＝·|xP－2|＝·.
∴＝＝·
＝≥2，当且仅当＝，即m＝±1时等号成立．
∴当m＝±1，即直线l的斜率为±1时，取得最小值2.

1．椭圆＋＝1与＋＝1(0 A．有相等的长轴 B．有相等的短轴
C．有相同的焦点 D．有相等的焦距
答案　D
解析　当0 2．点A(a,1)在椭圆＋＝1的内部，则a的取值范围是(　　)
A．－
C．－2 答案　A
解析　由已知可得＋<1，∴a2<2，即－ 3．(多选)设椭圆C：＋y2＝1的左、右焦点分别为F1，F2，P是C上的动点，则下列结论正确的是(　　)
A．|PF1|＋|PF2|＝2
B．椭圆C的离心率e＝
C．△PF1F2面积的最大值为
D．以线段F1F2为直径的圆与直线x＋y－＝0相切
答案　AD
解析　由椭圆C：＋y2＝1可知，a＝，b＝1，c＝1.|PF1|＋|PF2|＝2a＝2，A正确；椭圆C的离心率e＝＝，B错误；当P为椭圆C短轴的一个端点时，△PF1F2的面积最大，最大值为×2c×b＝1，C错误；原点(0,0)到直线x＋y－＝0的距离d＝＝1＝c，故以线段F1F2为直径的圆与直线x＋y－＝0相切，D正确．故选AD.
4．若直线y＝x＋1与椭圆＋y2＝1相交于A，B两个不同的点，则|AB|＝________.
答案　
解析　由解得A，B两个不同的点的坐标分别为(0,1)，，
故|AB|＝＝.
5．已知直线l：y＝2x＋m，椭圆C：＋＝1.试问当m取何值时，直线l与椭圆C：
(1)有两个公共点；
(2)有且只有一个公共点；
(3)没有公共点．
解　直线l的方程与椭圆C的方程联立，得方程组
消去y，得9x2＋8mx＋2m2－4＝0.①
方程①的判别式Δ＝(8m)2－4×9×(2m2－4)＝－8m2＋144.
(1)当Δ>0，即－3 (2)当Δ＝0，即m＝±3时，方程①有两个相同的实数解，可知原方程组有两组相同的实数解．这时直线l与椭圆C有且只有一个公共点．
(3)当Δ<0，即m<－3或m>3时，方程①没有实数解，可知原方程组没有实数解．这时直线l与椭圆C没有公共点．

A级：“四基”巩固训练
一、选择题
1．已知椭圆＋＝1(a>b>0)的离心率为，则(　　)
A．a2＝2b2 B．3a2＝4b2
C．a＝2b D．3a＝4b
答案　B
解析　因为椭圆的离心率e＝＝，所以a2＝4c2.
又a2＝b2＋c2，所以3a2＝4b2.故选B.
2．直线y＝x＋1被椭圆＋＝1所截得的线段的中点坐标为(　　)
A. B．
C. D．
答案　C
解析　由消去y，得3x2＋4x－2＝0.设直线与椭圆的交点A(x1，y1)，B(x2，y2)，则x1＋x2＝－，∴y1＋y2＝x1＋x2＋2＝.∴AB中点的坐标为.
3．若直线kx－y＋3＝0与椭圆＋＝1有两个公共点，则实数k的取值范围是(　　)
A．－ C．k>或k<－ D．k<且k≠－
答案　C
解析　由可得(4k2＋1)x2＋24kx＋20＝0，当Δ＝(24k)2－4×(4k2＋1)×20＝16(16k2－5)>0，即k>或k<－时，直线与椭圆有两个公共点．
4．椭圆＋y2＝1的两个焦点为F1，F2，过F1作垂直于x轴的直线与椭圆相交，一个交点为P，则|PF2|为(　　)
A. B．
C．4 D．
答案　D
解析　∵|PF1|＋|PF2|＝4，|PF1|＝＝，∴|PF2|＝4－＝.
5．过椭圆C：＋＝1的左焦点F作倾斜角为60°的直线l与椭圆C交于A，B两点，则＋等于(　　)
A. B．
C． D．
答案　A
解析　由已知得直线l：y＝(x＋1)．联立
可得A(0，)，B，又F(－1，0)，∴|AF|＝2，|BF|＝，∴＋＝.
6．(多选)已知F1，F2是椭圆的两个焦点，满足·＝0的点M总在椭圆内部，则椭圆的离心率可以是(　　)
A. B．
C． D．
答案　BC
解析　由·＝0知MF1⊥MF2，∴以F1F2为直径的圆包含在椭圆内部，∴椭圆上的点均满足∠F1MF2<90°，∴只需F1，F2与短轴端点形成的角为锐角，∴c 二、填空题
7．人造地球卫星的运行轨道是以地心为一个焦点的椭圆，设地球半径为R，卫星近地点、远地点离地面的距离分别为r1，r2，则卫星运行轨道的离心率是________.
答案　
解析　由题意得∴2a＝2R＋r1＋r2，2c＝r2－r1.∴e＝＝.
8．若点O和点F分别为椭圆＋＝1的中心和左焦点，点P为椭圆上的任意一点，则O·F的最大值为________.
答案　6
解析　由椭圆＋＝1可得F(－1,0)，O(0,0)．
设P(x，y)，－2≤x≤2，则O·F＝x2＋x＋y2＝x2＋x＋3＝x2＋x＋3＝(x＋2)2＋2，当且仅当x＝2时，O·F取得最大值6.
9．如图，已知F1，F2是椭圆C：＋＝1(a>b>0)的左、右焦点，点P在椭圆C上，线段PF2与圆x2＋y2＝b2相切于点Q，且点Q为线段PF2的中点，则椭圆C的离心率为________.

答案　
解析　连接OQ，F1P，则由切线的性质，知OQ⊥PF2，又点Q为线段PF2的中点，O为F1F2的中点，∴OQ∥F1P，∴PF2⊥PF1，|PF1|＝2|OQ|＝2b，故|PF2|＝2a－2b，又|F1F2|＝2c，|F1F2|2＝|PF1|2＋|PF2|2，则4c2＝4b2＋4(a2－2ab＋b2)，解得b＝a，则c＝a，故椭圆的离心率为.
三、解答题
10．已知F为椭圆＋＝1(a>b>0)的一个焦点，过原点的直线l与椭圆交于M，N两点，且·＝0，△MNF的面积为ab.
(1)求椭圆的离心率；
(2)若F(，0)，过点F且不与坐标轴垂直的直线交椭圆于A，B两点，线段AB的垂直平分线与x轴交于点G，求点G横坐标的取值范围．
解　(1)设椭圆的半焦距为c，另一个焦点为F1.
因为·＝0，所以MF⊥NF，
由椭圆的对称性可知四边形F1MFN为矩形，|MF1|＝|NF|，
所以得4a2＝4c2＋2ab，
又a2＝b2＋c2，所以a2＝c2，
即＝，椭圆C的离心率e＝.
(2)因为F的坐标为(，0)，
e＝，所以c＝，a＝2，
b2＝a2－c2＝4－3＝1，
故椭圆的方程为＋y2＝1.
因为直线AB不与坐标轴垂直，故设直线AB的斜率为k，
且k≠0，则直线AB的方程为y＝k(x－)，
将AB方程与椭圆方程联立得
消去y得(1＋4k2)x2－8k2x＋12k2－4＝0，
由根与系数的关系得，x1＋x2＝，
设线段AB的中点坐标为(x0，y0)，则
x0＝＝，
y0＝k＝.
则AB垂直平分线的方程为y－y0＝－(x－x0)．
令y＝0，G点横坐标为xG＝x0＋ky0＝－＝＝－，
因为k≠0，所以1＋4k2>1.
故点G横坐标的取值范围为.
B级：“四能”提升训练
1．设椭圆＋＝1(a>b>0)的左焦点为F，上顶点为B.已知椭圆的短轴长为4，离心率为.
(1)求椭圆的方程；
(2)设点P在椭圆上，且异于椭圆的上、下顶点，点M为直线PB与x轴的交点，点N在y轴的负半轴上．若|ON|＝|OF|(O为原点)，且OP⊥MN，求直线PB的斜率．
解　(1)设椭圆的半焦距为c，依题意，2b＝4，＝，
又a2＝b2＋c2，可得a＝，b＝2，c＝1.
所以椭圆的方程为＋＝1.
(2)由题意，设P(xP，yP)(xP≠0)，M(xM,0)．
设直线PB的斜率为k(k≠0)，
又B(0,2)，则直线PB的方程为y＝kx＋2，与椭圆方程联立得整理得(4＋5k2)x2＋20kx＝0，
可得xP＝－，
代入y＝kx＋2得yP＝，
进而直线OP的斜率＝.
在y＝kx＋2中，令y＝0，得xM＝－.
由题意得N(0，－1)，所以直线MN的斜率为－.
由OP⊥MN，得·＝－1，
化简得k2＝，
从而k＝±.
所以直线PB的斜率为或－.
2.如图，在平面直角坐标系xOy中，椭圆C：＋＝1(a>b>0)的焦点为F1(－1,0)，F2(1,0)．过F2作x轴的垂线l，在x轴的上方，l与圆F2：(x－1)2＋y2＝4a2交于点A，与椭圆C交于点D.连接AF1并延长交圆F2于点B，连接BF2交椭圆C于点E，连接DF1.已知|DF1|＝.

(1)求椭圆C的标准方程；
(2)求点E的坐标．
解　(1)设椭圆C的焦距为2c.
因为F1(－1,0)，F2(1,0)，所以|F1F2|＝2，c＝1.
又因为|DF1|＝，AF2⊥x轴，
所以|DF2|＝＝＝.
因此2a＝|DF1|＋|DF2|＝4，从而a＝2.
由b2＝a2－c2，得b2＝3.
因此椭圆C的标准方程为＋＝1.
(2)解法一：由(1)知，椭圆C：＋＝1，a＝2.
因为AF2⊥x轴，所以点A的横坐标为1.
将x＝1代入圆F2的方程(x－1)2＋y2＝16，
解得y＝±4.
因为点A在x轴上方，所以A(1,4)．
又F1(－1,0)，所以直线AF1：y＝2x＋2.
由得5x2＋6x－11＝0，
解得x＝1或x＝－.
将x＝－代入y＝2x＋2，得y＝－.
因此B.
又F2(1,0)，所以直线BF2：y＝(x－1)．
由得7x2－6x－13＝0，
解得x＝－1或x＝.
又因为E是线段BF2与椭圆的交点，所以x＝－1.
将x＝－1代入y＝(x－1)，得y＝－.
因此E.
解法二：由(1)知，椭圆C：＋＝1.
如图，连接EF1.

因为|BF2|＝2a，|EF1|＋|EF2|＝2a，
所以|EF1|＝|EB|，
从而∠BF1E＝∠B.
因为|F2A|＝|F2B|，
所以∠A＝∠B.
所以∠A＝∠BF1E，
从而EF1∥F2A.
因为AF2⊥x轴，所以EF1⊥x轴．
因为F1(－1,0)，由得y＝±.
又因为E是线段BF2与椭圆的交点，所以y＝－.
因此E.