2022-2023学年福建省南平市高一上学期期末质量检测数学试题（解析版）

南平市2022—2023学年第一学期高一期末质量检测

数学试题

一､选择题：本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的.

1. 若全集，集合，则图中阴影部分表示的集合是（）

A.  B.  C.  D.

【答案】D

【解析】

【分析】根据韦恩图所表示的集合为，按照并集和补集的运算求解即可.

【详解】集合，则

则图中阴影部分表示的集合是.

故选：D.

2. 若幂函数图象过点，则（）

A. 1 B. 2 C.  D.

【答案】C

【解析】

【分析】把点代入得到，再结合对数的运算，即可求得本题答案.

【详解】因为幂函数图象过点，所以，得，

所以.

故选：C

3. “”是“”的（）

A. 充分而不必要条件 B. 必要而不充分条件

C. 充要条件 D. 既不充分也不必要条件

【答案】A

【解析】

【分析】由，得；反之不成立．再由充分必要条件的判定判断.

【详解】由，得；

反之，由，得.

∴“”是“”的充分不必要条件.

故选：A.

4. 为了得到函数的图象，可以将函数的图象

A. 向左平移个单位长度 B. 向右平移个单位长度

C. 向左平移个单位长度 D. 向右平移个单位长度

【答案】D

【解析】

【详解】，据此可知，为了得到函数的图象，可以将函数的图象向右平移个单位长度.

本题选择D选项.

5. 函数的零点所在的区间是（）

A.  B.  C.  D.

【答案】C

【解析】

【分析】先判断函数单调递增，再根据零点存在性定理，即可得出结果.

【详解】因为和都是增函数，所以在上显然单调递增，

又，，

根据零点存在性定理可知的零点所在的区间是，

因为函数单调递增，所以有且仅有一个零点.

故选：C

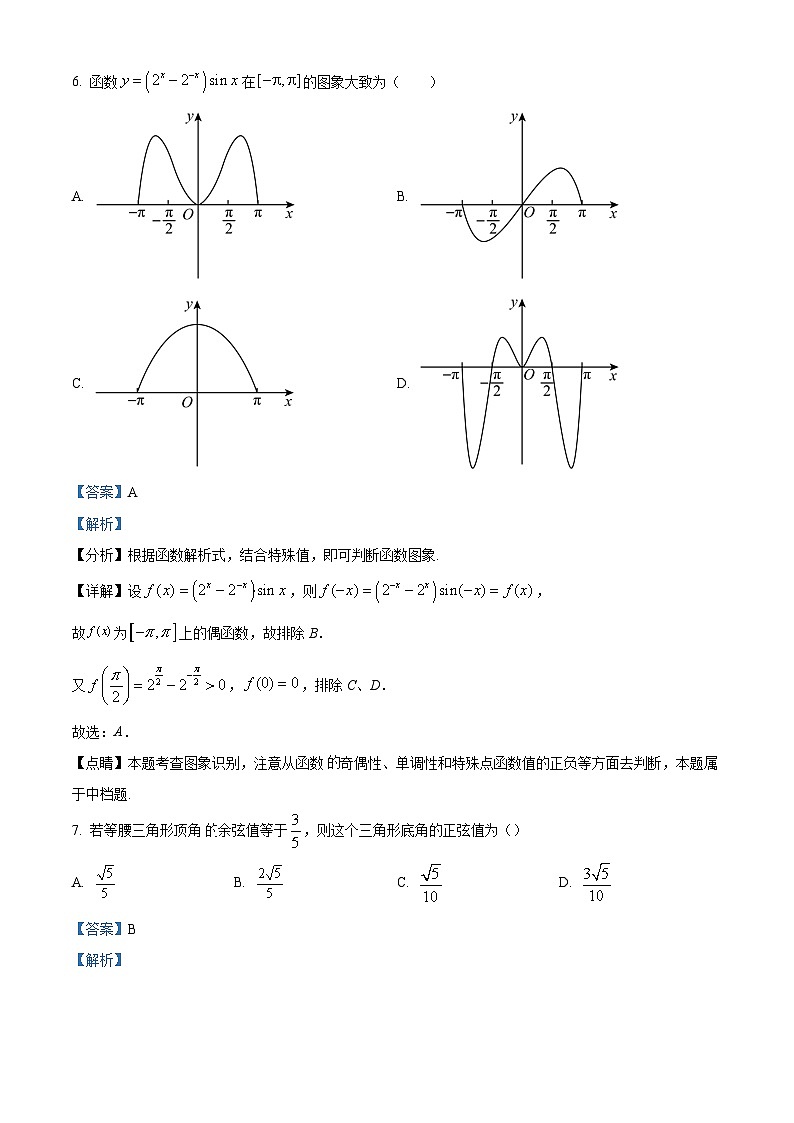
6. 函数在的图象大致为（    ）

A.  B.

C.  D.

【答案】A

【解析】

【分析】根据函数解析式，结合特殊值，即可判断函数图象.

【详解】设，则，

故为上的偶函数，故排除B．

又，，排除C、D．

故选：A．

【点睛】本题考查图象识别，注意从函数奇偶性、单调性和特殊点函数值的正负等方面去判断，本题属于中档题.

7. 若等腰三角形顶角余弦值等于，则这个三角形底角的正弦值为（）

A.  B.  C.  D.

【答案】B

【解析】

【分析】由结合倍角公式求解即可.

【详解】设顶角为，，则为锐角.

则这个三角形底角的正弦值为.

故选：B

8. 若，则（）

A.  B.  C.  D.

【答案】B

【解析】

【分析】借用中间值，可比较它们的大小，即可得到本题答案.

【详解】因为，所以，

因为，所以，

因为，所以，

所以.

故选：B

二､多选题：本题共4小题，每小题5分，共20分.在每小题给出的四个选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.

9. 下列命题正确的有（）

A. 若，则 B. 若，则

C. 若，则 D. 若，则

【答案】BD

【解析】

【分析】利用不等式的性质、特值法和基本不等式逐个选项进行判定即可.

【详解】对于A选项，当时，满足，但是，故A不正确；

对于B选项，根据不等式的性质可知准确，故B正确；

对于C选项，当时，满足，但是，故C不正确；

对于D选项，因为，所以，，当且仅当，即时，等号成立，故D正确；

故选：BD.

10. 函数的部分图象如图所示，则下列结论正确的是（）

A.  B.

C. 函数关于对称 D. 函数在上是增函数

【答案】BC

【解析】

【分析】由周期得出，由点得出，再由正弦函数的性质逐一判断即可.

【详解】因为在同一周期内，函数在时取得最大值，时取得最小值，

所以函数的最小正周期T满足，由此可得，解得；

得函数表达式为，又因为当时取得最大值2，

所以，可得，

因为，所以取，得，

所以，故A错误；

，故B正确；

令，所以函数关于对称，故C正确；

令，解得，令，则其中一个单调增区间为.故D错误.

故选：BC

11. 若定义在上的奇函数满足，且当时，，则（）

A. 为偶函数 B. 在上单调递增

C. 在上单调递增 D. 最小正周期

【答案】ABD

【解析】

【分析】由可得函数图象关于对称，通过图象的平移判断选项A正确；由函数为奇函数结合，可得函数的周期为，判断选项D正确；由时，，结合函数的奇偶性和对称性，可得函数的单调性，判断出B正确，C错误．

【详解】由得函数的图象关于对称，函数的图象是由函数的图象向左平移一个单位长度得到的，所以函数的图像关于y轴对称，所以函数是偶函数，故A正确；

由得，所以，的最小正周期为，故D正确；

当时，，因为是定义在上的奇函数，所以当时，，且，所以在上单调递增，在上单调递减，因为的最小正周期，所以在上单调递增，在上单调递减，故B正确，C错误.

故选：ABD

12. 已知函数，说法正确的是（）

A. 在区间上单调递增

B. 方程在的解为，且

C. 的对称轴是

D. 若，则

【答案】AB

【解析】

【分析】将函数写成分段函数，即可画出函数图象，再结合函数图象一一分析即可.

【详解】因为

，

即，

所以的图象如下所示：

，

由图可知函数是周期为的周期函数，函数在上单调递增，

所以在区间上单调递增，故A正确，

由图可知不是函数的对称轴，故C错误；

因为，所以与的交点即为所求，如图知有四个交点，

且，，

所以，故B正确.

由图象可知若，所以，，

则，，，，

所以，，，故D错误.

故选：AB

三､填空题：本题共4小题，每小题5分，共20分.

13. _______.

【答案】

【解析】

【分析】根据指数幂与对数的运算性质，准确运算，即可求解.

【详解】由指数幂与对数的运算性质，可得：

.

故答案为：.

14. 若是第二象限角，，则___________.

【答案】

【解析】

【分析】先确定属于第三象限，求出的值，然后利用公式展开，即可求得本题答案.

【详解】因为是第二象限角，且，

所以为第三象限角，所以，

所以.

故答案为：

15. 中国的5G技术领先世界，5G技术极大地提高了数据传输速率，最大数据传输速率C取决于信道带宽W，经科学研究表明：C与W满足，其中T为信噪比.若不改变带宽W，而将信噪比T从499提升到1999，则C大约增加________.（结果保留一位小数）

参考数据：.

【答案】22.3

【解析】

【分析】将与代入，作差后求增长率即可

【详解】当时，，

当时，

则，

所以C大约增加了，

即C大约增加了.

故答案为：22.3

16. 某市以市民需求为导向，对某公园进行升级改造，以提升市民的游园体验.已知公园的形状为如图所示的扇形区域，其半径为2千米，圆心角为，道路的一个顶点C在弧上.现在规划三条商业街道，要求街道与平行，交于点D，街道与垂直（垂足E在上），则街道长度最大值为___________千米.

【答案】

【解析】

【分析】设，利用几何关系得出，由勾股定理得出，再由正弦函数的性质得出长度的最大值.

【详解】过点作的垂线，垂足为，设，

则，

又，所以.

在直角三角形中，

，其中.

因为，所以，又，

所以当时，有最小值为，

即.

综上，街道长度的最大值为千米.

故答案为：

四､解答题：本题共6小题，共70分.解答应写出文字说明､证明过程或演算步骤.

17. 在平面直角坐标系中，角的终边与单位圆交于点，求下列各式的值.

（1）；

（2）.

【答案】（1）

（2）

【解析】

【分析】（1）由三角函数的定义，结合倍角公式计算即可；

（2）由诱导公式计算即可.

【小问1详解】

因为角的终边与单位圆交于点，所以.

；

【小问2详解】

.

18. 已知集合.

（1）求集合；

（2）若集合，且，求实数a的取值范围.

【答案】（1），，

（2）

【解析】

【分析】（1）解不等式求得集合,再根据并集的运算可求得.

（2）根据集合与集合的关系,可得关于a的不等式组,解不等式组即可求得参数a的取值范围.

【小问1详解】

等价于，解得，故集合.

等价于，解得，故集合.

所以.

【小问2详解】

由（1）可得集合，集合，所以.

于是，由，且得，解得，

即实数a的取值范围是.

19. 已知函数.

（1）求的最小正周期及单调递增区间；

（2）求在上最大值和最小值，并求出取得最值时x的值.

【答案】（1）最小正周期，单调递增区间是

（2）时，取得最小值；时，取得最大值1

【解析】

【分析】（1）由三角恒等变换化简解析式，进而由正弦函数的性质求解；

（2）由，结合正弦函数的性质求解即可.

【小问1详解】

.

所以的最小正周期.

令得

所以的单调递增区间是.

【小问2详解】

因为，所以，所以，故，所以当，即时，取得最小值；

当，即时，取得最大值1.

20. 某企业拟购买一批智能机器人生产A型电子元件，以提高生产效率，降低生产成本.已知购买x台机器人的总成本（万元）.

（1）要使所购买的机器人的平均成本最低，应购买多少台机器人？

（2）现将按（1）所求得的数量购买的机器人全部投入生产，并安排m名工人操作这些机器人（每名工人可以同时操作多台机器人）.已知每名工人操作水平无差异，但每台机器人每日生产A型电子元件的个数Q与操作工人人数有关，且满足关系式：.问在引进机器人后，需要操作工人的人数m为何值时，机器人日平均生产量达最大值，并求这个最大值.

【答案】（1）购买120台机器人；

（2）当大于等于20时，机器人日平均生产量达最大值，且最大值为19200个.

【解析】

【分析】(1)利用基本不等式即可求成本的最小值；

(2)根据分段函数讨论函数的最大值即可求解.

【小问1详解】

由总成本，

可得每台机器人的平均成本.

因为.

当且仅当，即时，等号成立.

所以要使所购机器人的平均成本最低，应购买120台机器人.

【小问2详解】

当时，120台机器人的日平均生产量为，

所以当时，120台机器人日平均生产量最大值为19200.

当时，120台机器人日平均生产量为.

所以120台机器人的日平均产量的最大值为19200个.

所以当大于等于20时，机器人日平均生产量达最大值，且最大值为19200个.

21. 函数定义在上的奇函数.

（1）求m的值；

（2）判断的单调性，并用定义证明；

（3）解关于x的不等式.

【答案】（1）

（2）在上单调递增，证明见解析

（3）答案见解析

【解析】

【分析】（1）由即可得解；

（2）由定义证明单调性即可；

（3）根据函数的奇偶性和单调性求解即可.

【小问1详解】

解法1：因为为定义在上的奇函数，

所以，所以，

得，即.

因为，所以，即.

解法2：因为为定义在上的奇函数，

所以.

当时，，

所以

【小问2详解】

在上单调递增.

由（1）得.

任取，

由于，又,所以，

所以在上单调递增.

【小问3详解】

由（2）得函数在上单调递增，且为奇函数，

所以不等式等价于

等价于，

等价于，

等价于

所以，当时，原不等式的解集为；

当时，原不等式的解集为；

当时，原不等式的解集为空集.

22. 已知函数且.

（1）若函数有零点，求a的取值范围；

（2）设函数，在（1）的条件下，若，使得，求实数m的取值范围.

【答案】（1）

（2）

【解析】

【分析】（1）函数有零点，即方程有解，则函数的图象与直线有交点，再分和两种情况讨论，即可得解；

（2），使得成立，即成立，利用基本不等式求出的最小值，分离参数，从而可得出答案.

【小问1详解】

若函数有零点，

即，即方程有解，

令，则函数的图象与直线有交点，

当时，，故方程无解，

当时，，

由方程有解可知，所以，

综上，a取值范围是；

【小问2详解】

当时，，

由（1）知，当且仅当，即时取等号，

所以的最小值是，

由题意，，使得成立，

即成立，

所以对恒成立，

设，则对恒成立，

设函数，

因为函数和函数在上都是减函数，

所以函数在上是减函数，

所以，所以，

即m的取值范围是.