2022-2023学年云南省昆明市云南民族大学附属中学高一上学期期末诊断测试数学试题（解析版）

2022-2023学年云南省昆明市云南民族大学附属中学高一上学期期末诊断测试数学试题

一、单选题

1．已知集合，集合，，则等于（    ）．

A．R B． C． D．

【答案】C

【分析】解不等式化简集合A，求出函数的值域化简集合B，再利用补集、交集的定义求解作答.

【详解】解不等式得：，即，，，即，

于是得，所以.

故选：C

2．函数的零点个数为

A．3 B．2 C．1 D．0

【答案】B

【详解】由，由，

所以函数的零点个数为2，故选B.

3．《掷铁饼者》取材于希腊的体育竞技活动，刻画的是一名强健的男了在掷铁饼过程中最具有表现力的瞬间.现在把掷铁饼者张开的双臂近似看成一张拉满弦的“弓”，掷铁饼者的一只手臂长约为米，整个肩宽约为米.“弓”所在圆的半径约为1.25米.则掷铁饼者双手之向的距离约为（    ）(参考数据：)

A．1.612米 B．1.768米 C．1.868米 D．2.045米

【答案】B

【解析】根据弧长公式求出圆心角为直角，再根据勾股定理可求得弦长.

【详解】由题得：“弓”所在的弧长为：；，

所以其所对的圆心角；

∴两手之间的距离.

故选：B.

4．函数的图象（    ）

A．关于轴对称 B．关于轴对称

C．关于坐标原点对称 D．关于直线对称

【答案】B

【分析】利用分离常数法化简函数式，可知函数为偶函数，进而判断对称性.

【详解】解：因为，

易知为偶函数，

所以函数的图象关于轴对称.

故选：B.

【点睛】本题考查函数的对称性，结合奇偶性的判断，考查分析问题能力，属于基础题.

5．已知非零向量，则“”是“”的（    ）

A．充分不必要条件 B．必要不充分条件

C．充分必要条件 D．既不充分又不必要条件

【答案】B

【分析】考虑两者之间的推出关系后可得两者之间的条件关系.

【详解】如图所示，,当时，与垂直，，所以成立，此时，

∴不是的充分条件，

当时，，∴,∴成立，

∴是的必要条件，

综上，“”是“”的必要不充分条件

故选：B.

6．若实数，，互不相等，且满足，则（    ）

A． B． C．， D．，

【答案】D

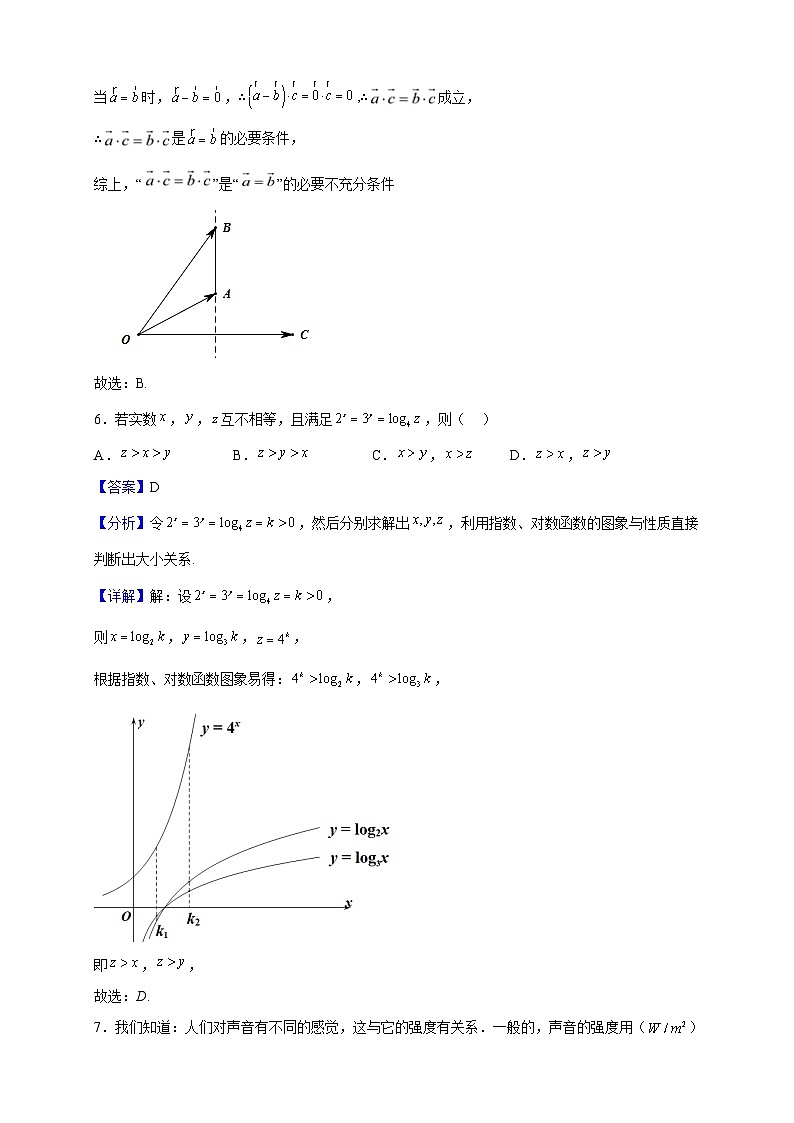
【分析】令，然后分别求解出，利用指数、对数函数的图象与性质直接判断出大小关系.

【详解】解：设，

则，，，

根据指数、对数函数图象易得：，，

即，，

故选：D.

7．我们知道：人们对声音有不同的感觉，这与它的强度有关系．一般的，声音的强度用（）表示，但在实际测量时，声音的强度水平常用（单位：分贝，，其中是人们平均能听到的最小强度，是听觉的开端）．某新建的小区规定：小区内公共场所的声音的强度水平必须保持在50分贝以下，则声音强度的取值范围是（     ）

A． B． C． D．

【答案】C

【分析】根据小区内公共场所的声音的强度水平必须保持在50分贝以下，建立不等式，然后解对数不等式即可得到答案．

【详解】解：由题意可得，，即，

所以，解得，

所以声音强度的取值范围是，．

故选：C．

8．已知具有性质：的函数，我们称为满足“倒负”变换的函数，下列函数：①；②；③.其中满足“倒负”变换的函数是（     ）

A．①② B．①③ C．②③ D．①

【答案】B

【分析】对于①②直接用定义验证，对于③因其是分段函数，所以应分段验证．

【详解】解：对于①，，满足“倒负”变换；

对于②，；

不满足“倒负”变换；

对于③，当时，，

当时，，

当时，，

满足“倒负”变换．

故选：B．

【点睛】考查新定义型题，这类题的特点是依据定义来进行运算或判断，故审题中认真了解定义是做题的关键，属于基础题．

二、多选题

9．设函数的图象为曲线，则下列结论中正确的是（    ）

A．是曲线的一个对称中心

B．若，且，则的最小值为

C．将曲线向右平移个单位长度，与曲线重合

D．将曲线上各点的横坐标缩短到原来的，纵坐标不变，与曲线重合

【答案】BD

【分析】由题意利用函数的图象变换规律，正弦函数的图象和性质，得出结论.

【详解】函数的图象为曲线，

令，求得，为最小值，故的图象关于直线对称，故A错误；

若，且，则的最小值为，故B正确；

将曲线向右平移个单位长度，可得的图象，故C错误；

将曲线上各点的横坐标缩短到原来的，纵坐标不变，可得的图象，与曲线E重合，故D正确，

故选：BD.

10．已知正实数，满足，，且，则下列不等式成立的有（    ）

A． B．

C． D．

【答案】AB

【分析】选项A，由直接由均值不等式可得，从而可判断；选项B，由条件可得，从而可判断；选项C，由，利用均值不等式，从而可判断；选项D，直接利用均值不等式可判断.

【详解】∵，当且仅当a＝b时取等号，∴A正确；

∵，∴B正确；

∵＋＝(a＋b)＝≥2＋2＝4，

当且仅当a＝b时取等号，∴C错误；

∵，，，∴，∵，

当且仅当a＝1时取等号，∴，D错误.

故选：AB.

11．已知函数，则下列结论正确的是（    ）

A．在上为增函数

B．

C．若在上单调递增，则或

D．当时，的值域为

【答案】BC

【分析】结合分段函数的单调性对选项逐一辨析即可.

【详解】易知在(－∞，0]，(0，＋∞)上单调递增，A错误，

，，B正确；

若在(a，a＋1)上单调递增，则或，即或，故C正确；

当时，，当时，，

故时，的值域为，故D错误.

故选：BC.

12．在数学中，布劳威尔不动点定理可应用到有限维空间，并是构成一般不动点定理的基石，它得名于荷兰数学家鲁伊兹·布劳威尔(L.E.J.Brouwer)，简单的讲就是对于满足一定条件的连续函数，存在一个点，使得，那么我们称该函数为“不动点”函数，下列为“不动点”函数的是（    ）

A． B．

C． D．

【答案】BCD

【分析】根据题中“不动点”函数所给定义，只需判断是否有解即可

【详解】对于A：由题意，所以，此方程无解，所以A中函数不是“不动点”函数；

对于B：由题意，即，记，因为，，，，由零点存在性定理知，函数在区间和区间上有零点，即方程有解，故B中函数是“不动点”函数；

对于C：由题意，解得：，所以C中函数是“不动点”函数；

对于D：，在同一直角坐标系下画出函数以及的图像，可确定两个函数的图像有交点，即方程有解，所以D中函数是“不动点”函数；

故选：BCD.

三、填空题

13．已知幂函数的图象过点，则___________.

【答案】

【分析】由幂函数的解析式的形式可求出和的值，再将点 代入可求的值，即可求解.

【详解】因为是幂函数，

所以，，又的图象过点，

所以，解得，

所以.

故答案为：.

14．已知＝，则sin2x＝________．

【答案】

【分析】利用诱导公式、二倍角余弦公式得sin2x＝2cos2－1，结合已知求值即可.

【详解】∵sin2x＝cos＝cos2＝2cos2－1，

∴sin2x＝2×－1＝－1＝．

故答案为：

15．若对时，不等式恒成立，则实数的取值范围是____________..

【答案】

【解析】运用换元法,参变分离法来求解不等式恒成立问题.

【详解】不等式转化为,化简为，

令,又,则,

即恒成立，令，又，

当时，取最小值，

所以，恒成立,化简得，解不等式得.

故答案为：

【点睛】方法点晴：本题考查了不等式恒成立问题,在求解过程中运用了参变分离法,注意题目中变量的取值范围.

16．函数的零点个数为_________．

【答案】2

【详解】因为

所以函数的零点个数为函数与图象的交点的个数，

函数与图象如图，由图知，两函数图象有2个交点，

所以函数有2个零点．

【解析】二倍角的正弦、余弦公式，诱导公式，函数的零点．

四、解答题

17．设集合A={x|(x-3)(x-a)=0，a∈R}，B={x|(x-4)(x-1)=0}.

（1）若a=1时，求A∩B，A∪B；

（2）设C=A∪B，若集合C的子集有8个，求实数a的取值集合.

【答案】（1）A∩B={1}，A∪B={1，3，4}；（2）{1，3，4}.

【分析】（1）当时，，，，，由此能求出，；

（2）由，集合的子集有8个，得到集合中有3个元素，由此能求出实数的取值集合．

【详解】解：（1）由集合A={x|(x-3)(x-a)=0，a∈R}，

B={x|(x-4)(x-1)=0}，

所以当a=1时，A={1，3}，B={1，4}，

所以A∩B={1}，A∪B={1，3，4}.

（2）因为C=A∪B，集合C的子集有8个，所以集合C中有3个元素，而1，3，4∈C，故实数a的取值集合为{1，3，4}.

【点睛】本题考查交集、并集、实数的取值集合的求法，考查交集、补集定义、不等式性质等基础知识，考查运算求解能力，是基础题．

18．已知函数.

(1)求f(x)的定义域与最小正周期;

(2)设，若，求α的大小.

【答案】(1)x∈Rx≠,k∈Z,

(2)α=

【分析】(1)根据正切函数性质求定义域与最小正周期；

(2)根据两角和正切公式以及二倍角余弦公式化简等式为sin 2α=，再根据角范围求结果.

【详解】（1）由2x++kπ，k∈Z，得x≠，k∈Z,

所以f(x)的定义域为x∈Rx≠，k∈Z.

f(x)的最小正周期.

（2）由=2cos 2α，得tan=2cos 2α,

即，

整理得.

因为α∈,所以sin α+cos α≠0.

因此(cos α-sin α)2=,即sin 2α=.

由α∈，得2α∈，所以2α=，即α=.

19．已知二次函数f（x）的最小值为1，且f（0）＝f（2）＝3．

（1）求f（x）的解析式；

（2）若f（x）在区间[2a，a+1]上不单调，求实数a的取值范围；

（3）在区间[﹣1，1]上，y＝f（x）的图象恒在y＝2x+2m+1的图象上方，试确定实数m的取值范围．

【答案】（1）；（2）；（3）.

【分析】（1）根据题意，设，根据，求得，即可得到函数的解析式；

（2）由函数在区间上不单调，利用二次函数的性质，得到，即可求解；

（3）把区间上，的图象恒在的图象上方，转化为不等式在区间上恒成立，令，结合二次函数的性质，即可求解.

【详解】（1）由题意，函数是二次函数，且，可得函数对称轴为，

又由最小值为1，可设，

又，即，解得，

所以函数的解析式为.

（2）由（1）函数的对称轴为，

要使在区间上不单调，则满足，解得，

即实数的取值范围是.

（3）由在区间上，的图象恒在的图象上方，

可得在区间上恒成立，

化简得在区间上恒成立，

设函数，

则在区间上单调递减

∴在区间上的最小值为，

∴.

【点睛】本题主要考查了二次函数解析式的求解，以及二次函数的图象与性质综合应用，其中解答中熟练应用二次函数的图象与性质，合理转化是解答的关键，着重考查了转化思想，以及推理与运算能力，属于中档试题.

20．已知函数．

（1）求函数的最小正周期和单调递增区间；

（2）若函数所在上有两个不同的零点，，求实数的取值范围，并计算的值．

【答案】（1）最小正周期为，单调递增区间为：[，]，k∈Z；（2）m∈[，2），tan（x1′+x2′）＝．

【分析】（1）利用正弦和角公式，降幂扩角公式以及辅助角公式化简函数解析式为标准正弦型函数，再求函数性质即可；

（2）数形结合，根据图象有2个交点，求得的范围；根据对称性，即可求得，再求正切即可.

【详解】函数f（x）＝4sin（x）cosx．

化简可得：f（x）＝2sinxcosx﹣2cos2x

＝sin2x（cos2x）

＝sin2xcos2x

＝2sin（2x）

（1）函数的最小正周期T，

由2x时单调递增，

解得：

∴函数的单调递增区间为：[，]，k∈Z．

（2）函数g（x）＝f（x）﹣m所在[0，]匀上有两个不同的零点x1′，x2′，

转化为函数f（x）与函数y＝m有两个交点

令u＝2x，∵x∈[0，]，∴u∈[，]

可得f（x）＝sinu的图象（如图）．

从图可知：m在[，2），函数f（x）与函数y＝m有两个交点，

其横坐标分别为x1′，x2′．

故得实数m的取值范围是m∈[，2），

由题意可知x1′，x2′是关于对称轴是对称的：

那么函数在[0，]的对称轴x

∴x1′+x2′2

那么：tan（x1′+x2′）＝tan

【点睛】本题考查利用三角恒等变换化简三角函数，涉及三角函数性质的性质的求解，数形结合的思想，属综合中档题.

21．已知函数f(x)=log9(9x+1)+kx是偶函数.

（1）求k的值；

（2）若方程f(x)x+b有实数根，求b的取值范围；

【答案】（1）；（2）b>0.

【分析】（1）由题意结合偶函数的性质化简可得恒成立，运算即可得解；

（2）由题转化条件得有实数根，由对数的运算法则可得，再由函数单调性即可得解.

【详解】（1）因为y=f (x)为偶函数，

所以∀x∈R，，即对于∀x∈R恒成立，

所以恒成立，

所以恒成立，而x不恒为零，所以；

（2）由题意即有实数根，

令，则有实数根，

因为，

所以g(x)在是减函数，

又，所以g(x)>0，

若有实数根，则b>0.

【点睛】本题考查了函数奇偶性、对数运算法则及对数函数性质的应用，考查了函数与方程的综合应用及转化化归思想，属于中档题.

22．近年来，我国大部分地区遭遇雾霾天气，给人们的健康、交通安全等带来了严重影响.经研究发现工业废气等污染物排放是雾霾形成和持续的重要因素，污染治理刻不容缓.为此，某工厂新购置并安装了先进的废气处理设备，使产生的废气经过过滤后排放，以降低对空气的污染.已知过滤过程中废气的污染物数量（单位：mg/L）与过滤时间（单位：h）间的关系为（，均为非零常数，e为自然对数的底数），其中为时的污染物数量.若经过5h过滤后还剩余90%的污染物.

（1）求常数的值；

（2）试计算污染物减少到40%至少需要多长时间.（精确到1h，参考数据：，，，，）

【答案】（1）（2）42h

【分析】（1）根据题意，得到，求解，即可得出结果；

（2）根据（1）的结果，得到，由题意得到，求解，即可得出结果.

【详解】（1）由已知得，当时，；当时，.

于是有，解得（或）.

（2）由（1）知，当时，有，

解得.

故污染物减少到40%至少需要42h.

【点睛】本题主要考查函数模型的应用，熟记指数函数的性质即可，属于常考题型.