还剩3页未读，继续阅读

下载需要5学贝 1学贝=0.1元

使用下载券免费下载

加入资料篮

立即下载

辽宁省锦州市2023届高三质量监测数学试题（最后一模）(无答案)

展开

这是一份辽宁省锦州市2023届高三质量监测数学试题（最后一模）(无答案)，共6页。试卷主要包含了已知集合，则，已知直线的倾斜角为，则，若，则，已知，则等内容，欢迎下载使用。

2023年普通高校招生统一考试模拟试题

数学

一､单项选择题：本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的.

1.已知集合，则（）

A. B. C. D.

2.已知是空间两个不同的平面，命题“”，命题：“平面内有无数条直线与平行”，则是的（）

A.充分而不必要条件 B.必要而不充分条件

C.充分必要条件 D.既不充分也不必要条件

3.已知复数为虚数单位为纯虚数，则在复平面内，对应的点的轨迹为（）

A.圆 B.一条线段 C.两条直线 D.不含端点的4条射线

4.已知直线的倾斜角为，则（）

A.-3 B. C. D.

5.南宋晩期的龙泉窑粉青釉刻花斗笠盏如图1所示，这只杯盏的轴截面如图2所示，其中光滑的曲线是抛物线的一部分，已知杯盏盛满茶水时茶水的深度为，则该杯盏的高度为（）

A. B. C. D.

6.若，则（）

A.1 B.-1 C.19 D.-19

7.在中，，点在线段上，，点是外接圆上任意一点，则最大值为（）

A. B. C. D.

8.已知，则（）

A. B.

C. D.

二､多项选择题：本大题共4小题，每小题5分，共20分，在每小题给出的四个选项中，有多个选项是符合题目要求的.全部选对得5分，部分选对得2分，有选错的得0分.

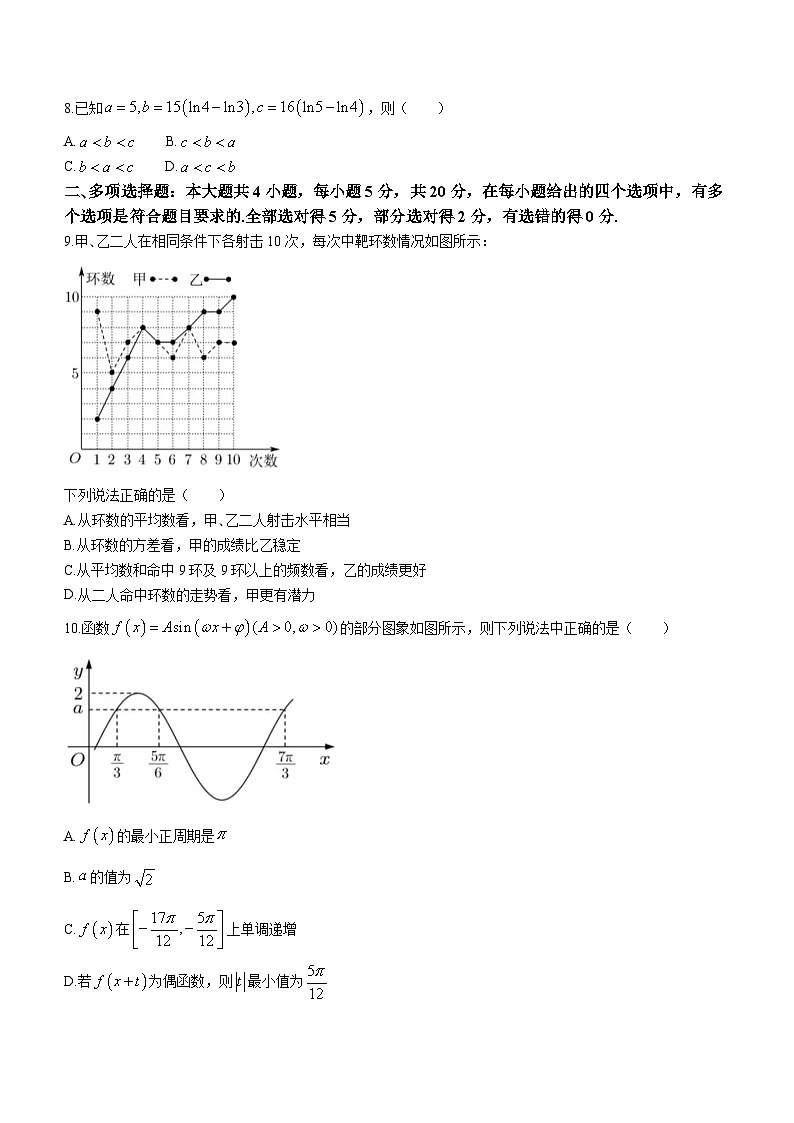
9.甲､乙二人在相同条件下各射击10次，每次中靶环数情况如图所示：

下列说法正确的是（）

A.从环数的平均数看，甲､乙二人射击水平相当

B.从环数的方差看，甲的成绩比乙稳定

C.从平均数和命中9环及9环以上的频数看，乙的成绩更好

D.从二人命中环数的走势看，甲更有潜力

10.函数的部分图象如图所示，则下列说法中正确的是（）

A.的最小正周期是

B.的值为

C.在上单调递增

D.若为偶函数，则最小值为

11.若是函数（e为自然对数的底数）图象上的任意两点，且函数在点和点处的切线互相垂直，则下列结论中正确的是（）

A. B.最小值为1

C.的最小值为 D.的最大值为

12.如图，正方体的棱长为3，点分别在棱上，满足，记平面与平面的交线为，则（）

A.存在使得平面截正方体所得截面图形为四边形

B.当时，三棱锥的外接球表面积为

C.当时，三棱锥体积为

D.当时，与平面所成的角的正弦值为

三､填空题：本大题共4小题，每小题5分，共20分.

13.某考生回答一道有4个选项的选择题，设会答该题的概率是，并且会答时一定能答对，若不会答，则在4个答案中任选1个.已知该考生回答正确，则他确实会答该题的概率是__________.

14.设为定义在上的可导函数，其导函数为偶函数，若对任意有，且，则__________.

15.已知正项等差数列，公差为，前项和为，若也是公差为的等差数列，则__________.

16.已知分别为椭圆的左､右焦点，为椭圆上的动点，点关于直线的对称点为，点关于直线的对称点为，则当最大时，的面积为__________.

四､解答题：本题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤.

17.（10分）

在直角梯形中（如图一），.将沿折起，使（如图二）.

（1）求证：平面平面；

（2）设为线段的中点，求点到直线的距离.

18.（12分）

在中，角是锐角，角所对的边分别记作，满足，.

（1）求；

（2）若，求的值.

19.（12分）

记为数列的前项和，已知.

（1）求的通项公式；

（2）设单调递增的等差数列满足，且成等比数列.

（i）求的通项公式；

（ii）设，证明：.

20.（12分）

据相关机构调查表明我国中小学生身体健康状况不容忽视，多项身体指标（如肺活量､柔韧度､力量､速度､耐力等）自2000年起呈下降趋势，并且下降趋势明显，在国家的积极干预下，这种状况得到遏制，并向好的方向发展，到2019年中小学生在肺活量､柔韧度､力量､速度､耐力等多项指标出现好转，但肥胖､近视等问题依然严重，体育事业任重道远.某学校为提高学生身体素质，日常组织学生参加中短跑锻炼，学校在一次百米短跑测试中，抽取200名女生的成绩（单位：秒）作为样本，整理得到如图所示的频率分布直方图.