
数学人教版8年级下册期末复习真题汇编卷06矩形
展开数学人教版8年级下册
期末复习真题汇编卷
矩形
一、单选题
1.(2022秋·山东泰安·八年级校考期末)如图,以正方形的对角线为一边作菱形,则( )
A. B. C. D.
2.(2023春·江苏·八年级期末)小明同学为班级设计如图所示的班徽,为正方形的中心,四块全等的阴影图形均为菱形.若,,三点共线,则图中阴影面积与空白面积之比为( )
A. B. C. D.
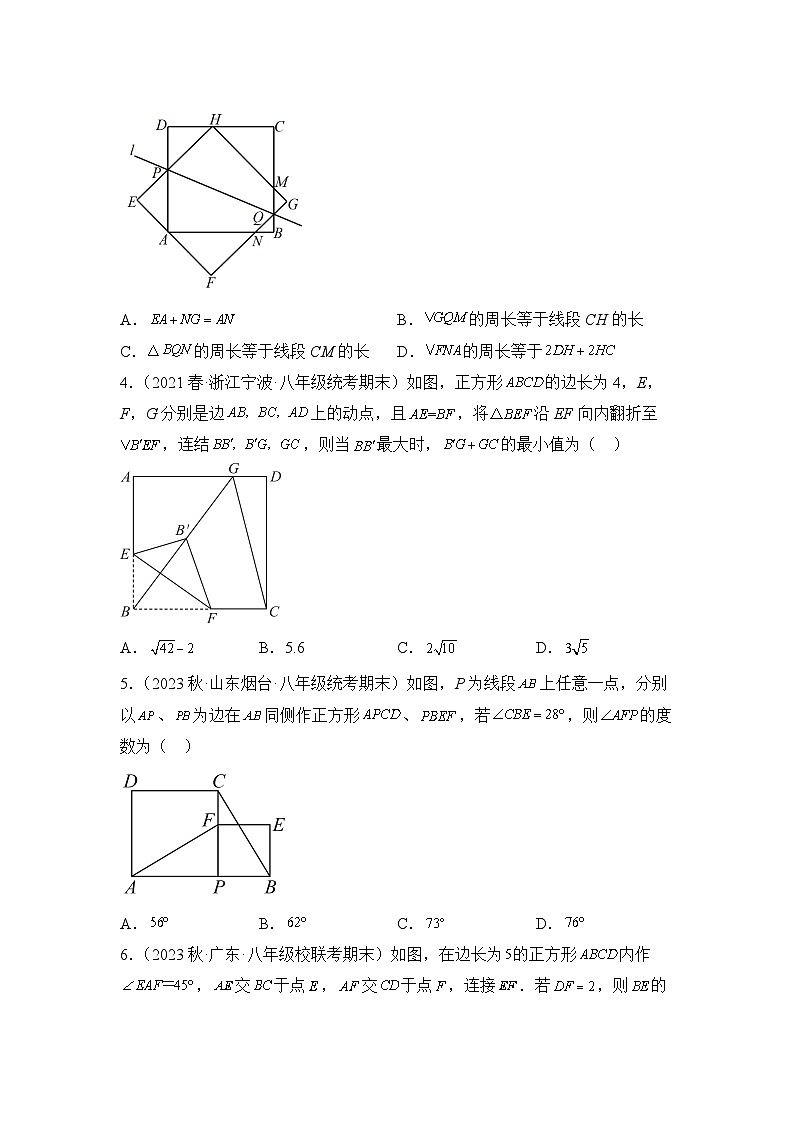
3.(2023春·浙江·八年级期末)如图,直线l交正方形的对边、于点P、Q,正方形和正方形关于直线l成轴对称,点H在边上,点A在边上,、交于点M,、交于点N.以下结论错误的是( )
A. B.的周长等于线段CH的长
C.的周长等于线段CM的长 D.的周长等于
4.(2021春·浙江宁波·八年级统考期末)如图,正方形的边长为4,E,F,G分别是边上的动点,且,将沿EF向内翻折至,连结,则当最大时,的最小值为( )
A. B.5.6 C. D.
5.(2023秋·山东烟台·八年级统考期末)如图,P为线段上任意一点,分别以、为边在同侧作正方形、,若,则的度数为( )
A. B. C. D.
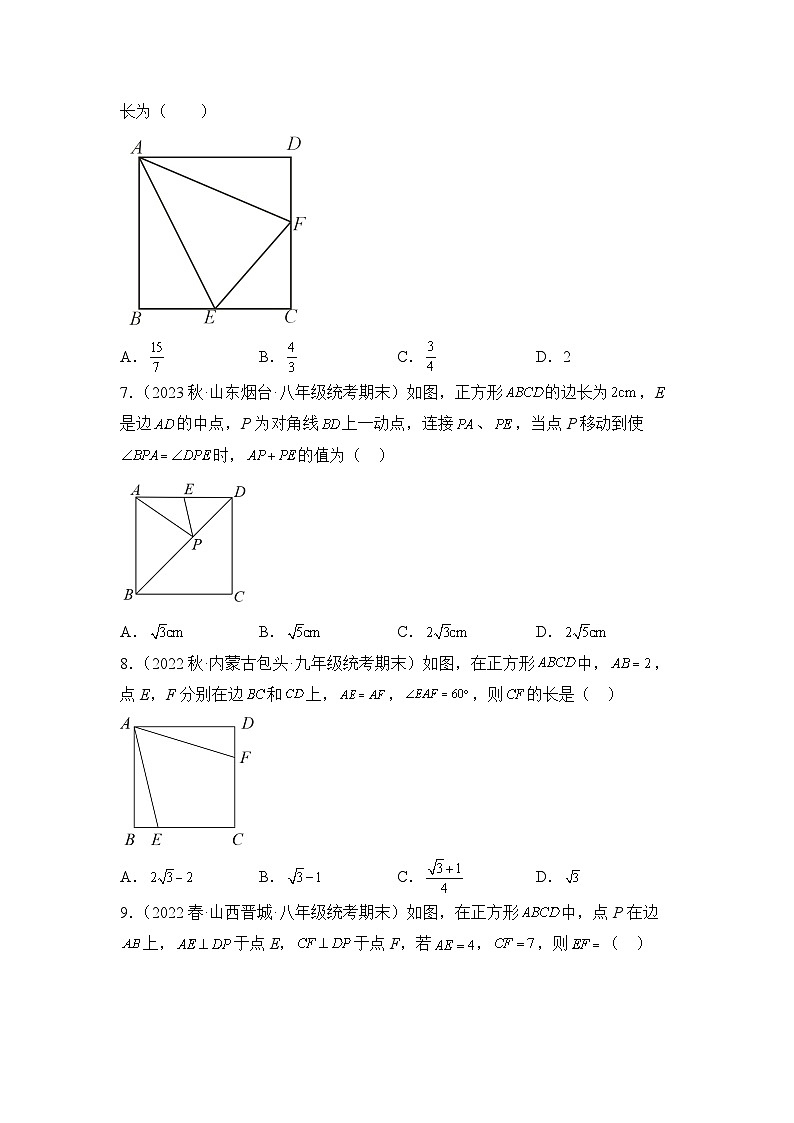
6.(2023秋·广东·八年级校联考期末)如图,在边长为的正方形内作,交于点,交于点,连接.若,则的长为( )
A. B. C. D.2
7.(2023秋·山东烟台·八年级统考期末)如图,正方形的边长为,E是边的中点,P为对角线上一动点,连接、,当点P移动到使时,的值为( )
A. B. C. D.
8.(2022秋·内蒙古包头·九年级统考期末)如图,在正方形中,,点E,F分别在边和上,,,则的长是( )
A. B. C. D.
9.(2022春·山西晋城·八年级统考期末)如图,在正方形中,点P在边上,于点E,于点F,若,,则( )
A.1 B.2 C.3 D.4
10.(2023秋·山东烟台·八年级统考期末)在边长为的正方形底座中,放置两张大小相同的正方形纸板,边在上,点,分别在上,若区域的周长比区域与区域的周长之和还大,则正方形纸板的边长为( )
A. B. C. D.
11.(2023秋·河北保定·九年级统考期末)在正方形中,点将对角线三等分,且,点E是正方形边上的一点,对于满足的点E的个数n进行探究,结论如下.结论1:若,则;结论2:若,则.下列判断正确的是( )
A.只有结论1正确 B.只有结论2正确
C.两个结论都正确 D.两个结论都不正确
12.(2023秋·四川宜宾·八年级统考期末)如图,直线L上有三个正方形a,b,c,若正方形a的边长为1,正方形c的边长为3,则正方形b的面积为( )
A.4 B.9 C.10 D.11
13.(2022春·河北保定·八年级校考期末)如图,正方形和正方形中,点D在上,,H是的中点,那么的长是( )
A.2.5 B. C. D.2
14.(2022秋·河南郑州·九年级校联考期末)如图,正方形中,,点E,F分别为上一点,且,连接交对角线于点G,点P,Q分别为的中点,则的长为( )
A.6 B. C. D.
15.(2023秋·贵州六盘水·九年级统考期末)如图,正方形的对角线相交于点O,(两直角边长均大于的长度)绕点O旋转的过程中,与正方形重叠部分的面积( )
A.由小变大 B.由大变小 C.始终不变 D.先由大变小,然后又由小变大
二、填空题
16.(2023秋·山西太原·九年级期末)如图,在正方形中,,点E,F分别在边上,,点M在对角线上运动,连接和,则的最小值等于__________.
17.(2022秋·陕西榆林·九年级统考期末)如图,在正方形中,,对角线、交于点O,点E、F分别为边、上的动点(不与端点重合),且,连接、、,则线段的最小值为________.
18.(2022秋·陕西渭南·九年级统考期末)如图,正方形的对角线,相交于点,点是上任意一点,于点,于点,若,则的长的最小值为_________.
19.(2023秋·浙江湖州·九年级统考期末)如图,已知:正方形的顶点A在矩形的边上,矩形的顶点G在正方形的边上,正方形的边长为4,的长为5,则的长为_______.
20.(2022秋·河北保定·七年级校考期末)如图,在正方形外作等边,则___________.
21.(2023秋·四川雅安·九年级统考期末)如图,已知正方形的边长为,连接,,平分交于点E,则_______.
22.(2022秋·湖南永州·八年级统考期末)如图,在正方形中,P,Q分别为的中点,若,则大小为___________.
23.(2023秋·陕西渭南·九年级统考期末)如图,点E是边长为8的正方形的对角线上的一个动点(不与点B,D重合),连接,以为边向左侧作正方形,点P为的中点,连接,,与的延长线交于点H,在点E运动过程中,线段的最小值为______.
24.(2022春·山西晋城·八年级统考期末)若点是的中点,,将正方形沿折叠,使点恰好落在边的中点处,点的对应点为点,则折痕的长为________ .
25.(2022秋·河北石家庄·八年级校考期末)如图是“赵爽弦图”,、、和是四个全等的直角三角形,四边形和都是正方形.如果,,则___________;此时的值是___________.
26.(2022秋·黑龙江绥化·九年级统考期末)如图,将n个边长都为的正方形按如图所示摆放,点、、…、分别是正方形的中心,则n个这样的正方形重叠部分的面积和为________(用n的代数式表示)
27.(2023秋·四川乐山·八年级统考期末)欧几里得是古希腊著名数学家、欧氏几何学开创者.下面问题是欧几里得证明勾股定理的证法一小片段,同学们,让我们一起来走进欧几里得的数学王国吧!
如图,分别以的三边为边长,向外作正方形、、.
(1)连接、,则、的关系是______;
(2)过点作的垂线,交于点,交于点,若,,则正方形的边长是______.
28.(2023秋·辽宁阜新·九年级阜新实验中学校考期末)如图,已知,在内部作以点O为位似中心的正方形,正方形,正方形,…,正方形,其对应顶点,,,…都在射线上,对应顶点,,,…都在射线上,将正方形的面积记作;正方形的面积记作;正方形的面积记作;…,依此类推,正方形的面积记作,若,则第n个正方形的面积______.
29.(2023秋·黑龙江哈尔滨·九年级校考期末)如图,在正方形中,点,为,上的点,且,与交于点,连接,点为中点,连接,若,,则的长为________.
30.(2022秋·河南南阳·九年级统考期末)如图,正方形的边长为6,点,分别在,上,,连接、,与相交于点,连接,取的中点,连接,则的长为________.
三、解答题
31.(2023秋·山西太原·九年级期末)如图,在中,点M和N分别在边和上,,连接,点D,E,F,G分别是的中点.求证:四边形是菱形.
32.(2022春·江苏无锡·八年级统考期末)如图,正方形的边长为6,菱形的三个顶点E、G、H分别在正方形的边上,.
(1)如图1,当时,求证:菱形是正方形.
(2)如图2,连接,当的面积等于1时,求线段的长度.
33.(2023秋·山东泰安·八年级校考期末)如图,在正方形中,P是对角线上的一点,点E在的延长线上,且,交于F.
(1)证明:;
(2)求的度数;
34.(2021春·广东广州·八年级校考期末)在正方形中,点是边上任意一点.连接,过点作于.交于.
(1)如图1,过点作于,求证:;
(2)如图2,点为的中点,连接,求证:;
(3)如图3,,连接,点为的中点,在点从点运动到点的过程中,点随之运动,请直接写出点运动的路径长.
35.(2023春·广东广州·九年级广东实验中学校考期末)在正方形ABCD中,边长为2.点E是线段BC上的动点,以AE为直角边在直线BC的上方作等腰直角三角形AEF,,其中EF交CD于点P,AF交CD于点Q,连接CF.
(1)如图1,①若时,求线段CF的长:
②当点E在线段BC上运动时,求证:.
(2)如图2,过点B作交EQ于点G,过点D作所在的直线于点H,求HG的最小值.
36.(2021春·湖北武汉·八年级统考期末)如图,点G是正方形对角线的延长线上任意一点,以线段为边作一个正方形,线段和相交于点H.
(1)求证:;
(2)若,,求的长.
37.(2023秋·辽宁朝阳·八年级统考期末)如图,在边长为6的正方形中,E是边的中点.将沿对折至,延长交于点G,连接,平分.
(1)试说明
(2)求的长.
38.(2022秋·山东烟台·八年级统考期末)如图,在正方形中,点E是的中点,连接,过点A作交于点F,交于点G.
(1)证明:;
(2)连接,求证:.
39.(2022秋·内蒙古包头·九年级统考期末)如图,在正方形中,,M是对角线上的一个动点.连接,过点M作交于点N.
(1)如图1,求证:;
(2)如图2,过点N作于H,,求.
40.(2023秋·陕西咸阳·九年级统考期末)如图,在正方形中,点E为边上一点,延长至点G,使得,过点G作,连接、,且,求证:.
41.(2022秋·广东珠海·九年级统考期末)如图,将正方形绕顶点A顺时针旋转得到正方形,与相交于点E,连接,相交于点F.
(1)填空:______度;
(2)求证:四边形是菱形.
参考答案
1.D
2.A
3.C
4.C
5.B
6.A
7.B
8.A
9.C
10.B
11.B
12.C
13.B
14.D
15.C
16.6
17.
18.
19.
20.
21.
22./70度
23.
24.
25.
26.
27.
28.
29.
30.
31.证明:∵点,分别是,的中点,
∴是的中位线,
∴,,
同理可得:,,,
∴,,
∴四边形是平行四边形,
∵,
∴,
∴平行四边形为菱形.
32.(1)证明:∵四边形是正方形,
∴,
∵四边形是菱形,
∴,
在和中,
,
∴,
∴,
∵
∴,
∴,
∴菱形为正方形;
(2)解:过F作,交的延长线于点M,连接,
∵在正方形中,,
∴,
∵在菱形中,,,
∴,
∴;
在和中,
,
∴,
∴,
设,则,
∴,
∴,即.
33.(1)证明:∵四边形是正方形,
∴,
又∵,
∴,
∴,
∵,
∴;
(2)解:由(1)知,,
∴,
∵在正方形中,,
∴,即,
∵,
∴,
∴,
∵(对顶角相等),
∴,即.
34.(1)证明:四边形是正方形,
,,
,,
,
,,
,
在和中,
,
;
(2)证明:过点作于,交的延长线于,如图2所示:
四边形是正方形,
,,
,
,
,,
,
在和中,
,
∴,
,
点为的中点,
,
,
,
,,
,
四边形是矩形,
,
,
在和中,
,
∴,
,,
四边形是正方形,
,
,
;
(3)解:如图3,取的中点,连接,延长交于,过点作于,于,
设,
由(2)得:,
,
,点为的中点,
,
,,
,
四边形是矩形,
,,
,,,
,,
,
,,
,
,
是等腰直角三角形,
,
点在线段上运动,是等腰直角三角形,
,
点的运动的路径长为.
35.(1)解:如图,过点F作于点N,
是等腰直角三角形,
,,
,
,
,
(AAS),
,,
,
,
又,
是等腰直角三角形,
,
故答案是:;
证明:如图,延长CB至K,使,连接AK,
,,,
,
,,
,
,
,
又,
,
,
,
;
(2)解:如图,连接AG、GH、AH、AC,
由(1)得,,
四边形ABCD是正方形,
,,,
,
,,
是等腰直角三角形,
,
,
,
,,
,
,
又,
,
,
点G在以点A为圆心,AB长为半径的圆上,当点G在线段AH上时,GH有最小值,
最小值为,
故答案是:.
36.(1)解:
∵四边形和四边形是正方形,
∴,,,
在和中,,,
∴,
在和中,
,
∴;
(2)解:如图,连接,与交于点O,
由(1)得:
∴,
∵四边形是正方形,,
∴,
∴,
∵,
∴,
∴.
37.(1)在正方形中,,
∵将沿对折至,
∴,
∴,
又∵,
在和中,
,
∴().
(2)∵,
∴,
设,则,
∵E为的中点,
∴,
∴,
∴在中,,
解得,
∴.
38.(1)证明:∵四边形是正方形,
∴,,
又∵,
∴,
∴,
∴;
(2)证明:如图所示,延长交的延长线于H,
∵E是的中点,
∴,
又∵,,
∴,
∴,
即B是的中点,
又∵,
∴中,.
39.(1)证明:过点M作于F,作于G,如图1所示:
∴,
∵四边形是正方形,
∴,,,
∵,,
∴,
∵,
∴四边形是正方形,
∴,
∴,
∵,
∴,
∴,
在和中,
∴,
∴;
(2)解:过点A作于F,如图2所示:
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
在和中,
∴,
∴,在等腰直角中
∵,
∴,
∴.
40.证明:∵四边形正方形,
∴,,
∵,
∴,
∴,
∵,
∴,
在和中,,,
∴,
即.
41.(1)解:∵四边形和四边形是正方形
∴
∵
∴
∴
(2)解:连接.
∵四边形和四边形是正方形
∴
∵
∴
∴
(方法不唯一,直接写由(1)得也可以)
在正方形中,
∴
∴,即.
同理,
∴.
∴四边形是平行四边形
在和中
∴
∴
∴平行四边形是菱形.
数学人教版8年级下册期末复习真题汇编卷08数据的分析: 这是一份数学人教版8年级下册期末复习真题汇编卷08数据的分析,共19页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
数学人教版8年级下册期末复习真题汇编卷07一次函数: 这是一份数学人教版8年级下册期末复习真题汇编卷07一次函数,共25页。试卷主要包含了单选题,四象限,则一次函数的图象大致是,解答题等内容,欢迎下载使用。
数学人教版8年级下册期末复习真题汇编卷05菱形: 这是一份数学人教版8年级下册期末复习真题汇编卷05菱形,共19页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。












