

2022-2023学年广东省佛山市禅城区重点中学高一(下)期中数学试卷-普通用卷
展开
这是一份2022-2023学年广东省佛山市禅城区重点中学高一(下)期中数学试卷-普通用卷,共14页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
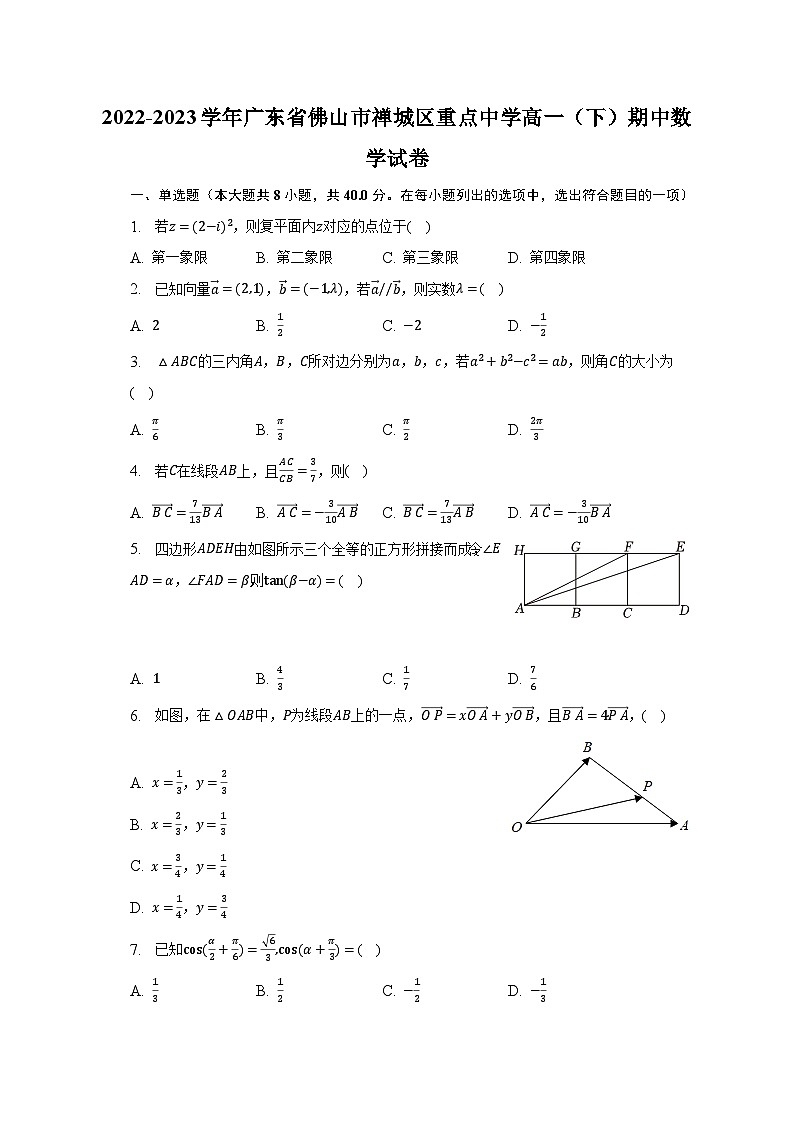
2022-2023学年广东省佛山市禅城区重点中学高一(下)期中数学试卷一、单选题(本大题共8小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)1. 若,则复平面内对应的点位于( )A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限2. 已知向量,,若,则实数( )A. B. C. D. 3. 的三内角,,所对边分别为,,,若,则角的大小为( )A. B. C. D. 4. 若在线段上,且,则( )A. B. C. D. 5. 四边形由如图所示三个全等的正方形拼接而成,令,,则( )
A. B. C. D. 6. 如图,在中,为线段上的一点,,且,( )
A. ,
B. ,
C. ,
D. ,7. 已知( )A. B. C. D. 8. 已知函数,则函数在区间上的最小值和最大值分别为( )A. , B. , C. D. ,二、多选题(本大题共4小题,共20.0分。在每小题有多项符合题目要求)9. 已知平面向量,,与的夹角为,则( )A. B.
C. D. 在上的投影向量的模为10. 下列说法正确的是( )A.
B. 圆心角为的扇形半径为,则该扇形的面积为
C. 底面是正多边形的棱锥是正棱锥
D. 长方体是直棱柱11. 已知函数的部分图像如图所示,则下列说法正确的是( )A. 最小正周期为
B. 直线是图像的一条对称轴
C. 点是图像的一个对称中心
D. 将的图像向左平移个单位长度后,图像关于轴对称
12. 在中,记角,,所对的边分别为,,,若,则( )A. B.
C. D. 内角的最大值为三、填空题(本大题共3小题,共15.0分)13. 在中,若,,,则的值为 .14. 若,则 ______ .15. 在中,,,点为边的中点,点在边上,则的最小值为______.四、解答题(本大题共7小题,共75.0分。解答应写出文字说明,证明过程或演算步骤)16. 本小题分、已知复数其中为虚数单位,则______. 17. 本小题分
设平面三点,,.
若,试求点的坐标;
试求向量与的夹角余弦值;18. 本小题分
已知复数,,若为纯虚数,求的值;
已知复数满足,求的值.19. 本小题分
已知的内角,,所对的边分别为,,,,,,且为钝角.
求;
求的面积.20. 本小题分
锐角三角形中,.,求的值.
已知求的值.21. 本小题分
已知内角,,的对边分别为,,,且.
求角;
若的周长为,且外接圆的半径为,求的面积.22. 本小题分
一年之计在于春,春天正是播种的好季节小林的爷爷对自己的一块正方形菜园做了一些计划如图,是边长为米的正方形菜园,扇形区域计划种植花生,矩形区域计划种植蔬菜,其余区域计划种植西瓜,分别在,上,在弧上,米,设矩形的面积为单位:平方米.
若,请写出单位:平方米关于的函数关系式;
求的最小值.
答案和解析 1.【答案】 【解析】解:由题意可得:,
所以复平面内对应的点为,位于第四象限.
故选:.
根据复数的四则运算化简复数,然后根据复数的几何意义判断.
本题主要考查复数的四则运算,属于基础题.
2.【答案】 【解析】解:由题设,故.
故选:.
由向量共线的坐标表示求参数即可.
本题主要考查了向量共线的坐标关系,属于基础题.
3.【答案】 【解析】【分析】本题考查利用余弦定理解三角形,属于基础题.
利用余弦定理即可得出.【解答】解:由余弦定理可得,
而,
.
故选B. 4.【答案】 【解析】解:在线段上且,
,,
则,,AB错误;
,,C错误,D正确.
故选:.
根据向量数乘运算的意义直接判断各个选项即可.
本题主要考查了向量的线性运算,属于基础题.
5.【答案】 【解析】解:依题意,设正方形的边长为,
根据正切函数的定义有:,
所以.
故选:.
由正切函数的定义即可求得,再根据正切的和差公式即可求解.
本题主要考查了两角差的正切公式的应用,属于基础题.
6.【答案】 【解析】解:在中,为线段上的一点,,且,
则:,
整理得:,
由于:,
所以:,.
故选:.
直接利用向量的共线的充要条件和向量的减法求出结果.
本题考查的知识要点:向量共线的充要条件,向量的线性运算,属于基础题型.
7.【答案】 【解析】解:由题意可得.
故选:.
以为整体,结合倍角公式求解即可.
本题主要考查了二倍角公式的应用,属于基础题.
8.【答案】 【解析】解:由题意可得:,
,则,
当,即,取到最小值;
当,即,取到最大值.
故选:.
根据三角恒等变换整理得,结合正弦函数求最值.
本题主要考查了二倍角公式,辅助角公式的应用,还考查了正弦函数性质的应用,属于中档题.
9.【答案】 【解析】解:,,与的夹角为,
对于,,故A正确;
对于:,
与不垂直,故B错误;
对于:,
,故C正确;
对于:在上的投影向量的模为,故D错误.
故选:.
根据平面向量的数量积的定义及数量积的运算律逐项判断.
本题主要考查平面向量的数量积运算,考查转化能力,属于中档题.
10.【答案】 【解析】解:对于:,且在内单调递减,
,即,故A错误;
对于:该扇形的面积为,故B正确;
对于:底面是正多边形,且侧棱长相等的棱锥是正棱锥,故C错误;
对于:侧棱垂直于底面的棱柱是直棱柱,所以长方体是直棱柱,故D正确.
故选:.
对于:根据余弦函数的性质分析判断;
对于:根据扇形的面积公式运算求解;
对于、:根据正棱锥、直棱柱的定义分析判断.
本题主要考查棱锥的结构特征、余弦函数、扇形面积公式,属于基础题.
11.【答案】 【解析】解:设函数的最小正周期为,
由图象可得:,
可得,故A正确;
则,且,解得,
可得,且图象过点,
可得,即,
,则,
可得,解得,
故.
不为最值,
则直线不是图像的一条对称轴,故B错误;
,
则点是图像的一个对称中心,故C正确;
将的图像向左平移个单位长度,得到,
且不是最值,
可知所得图像不关于轴对称,故D错误.
故选:.
根据图像最高点得到,由周期得到,再将点代入函数解析式中求得,再根据正弦型函数的图像性质,对选项逐一判断即可得到结果.
本题主要考查三角函数的图象与性质,考查转化能力,属于中档题.
12.【答案】 【解析】解:对于、:,故A选项错误,选项正确;
对于:因为,
所以,故C选项正确;
对于:因为,当且仅当时,等号成立,
所以,且,
所以,故内角的最大值为,故D选项正确.
故选:.
由向量的数量积公式计算判断、选项;结合余弦定理判断选项;由基本不等式和余弦函数的单调性判断选项.
本题主要考查平面向量的数量积运算,考查转化能力,属于中档题.
13.【答案】 【解析】解:因为,
由正弦定理,即,
所以,因为,
所以.
故答案为:.
由已知结合正弦定理计算可得.
本题主要考查了正弦定理在求解三角形中的应用,属于基础题.
14.【答案】 【解析】解:,
,
,
故答案为:.
根据二倍角的正弦公式及平方关系运算求解即可.
本题主要考查了二倍角公式及同角基本关系的应用,属于基础题.
15.【答案】 【解析】解:如图,
以为坐标原点,建立如图所示平面直角坐标系,
则,,,设,,
,,
可得,
当时,取最小值为.
故答案为:.
由题意画出图形,建立平面直角坐标系,利用平面向量数量积的坐标运算列式求解.
本题考查平面向量数量积的性质及运算,考查运算求解能力,建系是关键,是中档题.
16.【答案】略 【解析】解:,
.
故答案为:.
利用复数代数形式的乘除运算化简,然后代入复数模的计算公式求解.
本题考查复数代数形式的乘除运算,考查了复数模的求法,是基础题.
17.【答案】解:设,则,
因为,所以,解得,
所以点的坐标为.
由知,又,
所以,
故向量与的夹角余弦值为. 【解析】设,根据向量相等可列方程求解;
直接利用向量夹角公式即可求解.
本题主要考查了向量数量积的性质的坐标表示,属于中基础.
18.【答案】解:若为纯虚数,则,解得,
故的值为;
由题意可得:,
且,因此,解得,
故的值为. 【解析】根据复数的相关概念运算求解;
根据复数的四则运算结合模长公式运算求解.
本题主要考查复数的四则运算,属于基础题.
19.【答案】解:,,,
由正弦定理得,
,
又为钝角,;
,,
,又由知,
,又,,
的面积为. 【解析】根据正弦定理,即可求解;
由诱导公式和两角和的正弦公式得到,再根据三角形的面积公式,即可求解.
本题考查解三角形,正弦定理的应用,三角函数公式的应用,三角形面积公式的应用,属中档题.
20.【答案】解:因为,,且,为锐角,
所以,,
因为,则,
所以.
,
由,
所以原式. 【解析】根据同角三角关系结合诱导公式、两角和差公式运算求解;
根据诱导公式结合齐次式问题分析运算.
本题主要考查了同角基本关系,诱导公式在三角化简求值中的应用,属于中档题.
21.【答案】解:,
由正弦定理得,
因为,
所以,
因为,所以,所以,
又,所以.
设外接圆的半径为,则,
由正弦定理得,
因为的周长为,所以,
由余弦定理得,
即,所以,
所以的面积 . 【解析】由正弦定理及三角形的性质即可求角;
利用正弦定理求出边长,然后再根据周长和余弦定理列式解出,从而求解面积.
本题主要考查解三角形,考查转化能力,属于中档题.
22.【答案】解:延长交于,
则米,米,
则米,米,
.
由得:,
令,则,,
,
,
,
当时,,即当时,矩形面积的最小值为平方米. 【解析】延长交于,可用表示出,,由此可得;
令,将表示为关于的二次函数的形式,由二次函数最值的求法可求得结果.
本题主要考查函数的实际应用,考查转化能力,属于中档题.
相关试卷
这是一份2022-2023学年广东省佛山市顺德区重点学校高一(下)期中数学试卷,共18页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
这是一份2022-2023学年海南省海口重点中学高一(下)期中数学试卷-普通用卷,共17页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
这是一份2022-2023学年福建省莆田重点中学高一(下)期中数学试卷-普通用卷,共15页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。









