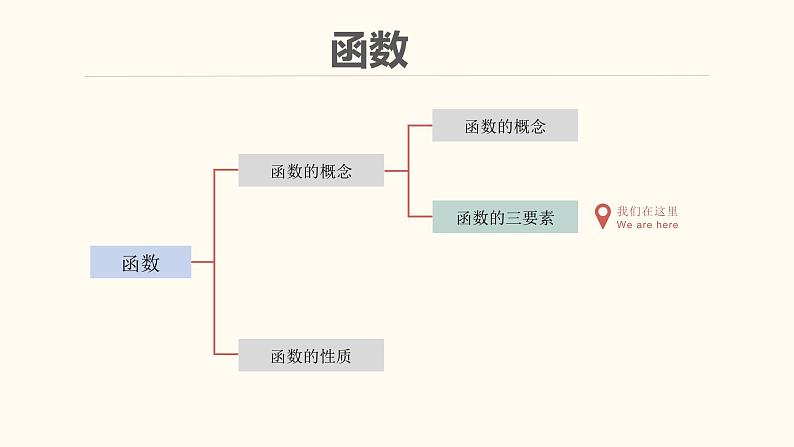
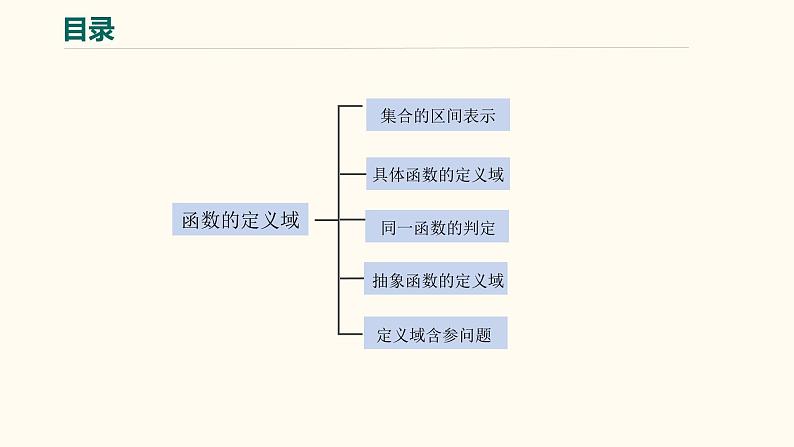
【暑假自学课】7.函数的定义域-2023年新高一数学暑假精品课（人教版2019必修第一册）课件PPT

【暑假自学课】11.函数的奇偶性-2023年新高一数学暑假精品课（人教版2019必修第一册）课件PPT： 这是一份【暑假自学课】11.函数的奇偶性-2023年新高一数学暑假精品课（人教版2019必修第一册）课件PPT，共49页。PPT课件主要包含了函数的奇偶性，奇偶性，对称美，我们生活在，一个对称的世界里，处处红花红处处，重重绿树绿重重，烷基八氮，奇偶性的概念，奇偶性的判断等内容，欢迎下载使用。

【暑假自学课】10.函数的单调性-2023年新高一数学暑假精品课（人教版2019必修第一册）课件PPT： 这是一份【暑假自学课】10.函数的单调性-2023年新高一数学暑假精品课（人教版2019必修第一册）课件PPT，共41页。PPT课件主要包含了函数单调性，单调性，单调性的概念，单调性概念的认识，P75，单调性的判断，P76，单调性小结，定义法证明单调性步骤，P77等内容，欢迎下载使用。

【暑假自学课】9.函数的值域-2023年新高一数学暑假精品课（人教版2019必修第一册）课件PPT： 这是一份【暑假自学课】9.函数的值域-2023年新高一数学暑假精品课（人教版2019必修第一册）课件PPT，共22页。PPT课件主要包含了函数值域，值域range，有界性，具体二次函数值域，换元二次函数值域，二次函数值域，分式型，双勾函数等内容，欢迎下载使用。