

福建省莆田市2021-2022学年高二下学期期末质量监测数学试卷(含答案)
展开福建省莆田市2021-2022学年高二下学期期末质量监测数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1、已知向量,且与互相垂直,则k的值为( )
A. -2 B. C. D. 2
2、甲、乙两名篮球运动员分别投篮一次,如果两人投中的概率都是0.6,且两人投篮相互独立,则两人都投中的概率为( )
A. 0.16 B. 0.24 C. 0.36 D. 0.6
3、函数的导函数是( )
A. B. C. D.
4、定义在上的函数,其导函数图像如图所示,则的单调递减区间是( )
A. B. C. D.
5、已知在空间直角坐标系中,平行四边形ABCD三个顶点的坐标分别为,则顶点D的坐标为( )
A. B. C. D.
6、“保护环境,绿色出行”是现代社会提倡的一种环保理念,李明早上上学的时候,可以乘坐公共汽车,也可以骑单车,已知李明骑单车的概率为0.7,乘坐公共汽车的概率为0.3,而且骑单车与乘坐公共汽车时,李明准时到校的概率分别为0.9与0.8,则李明准时到校的概率是( )
A. 0.9 B. 0.87 C. 0.83 D. 0.8
7、已知函数为增函数,则实数m的取值范围为( )
A. B. C. D.
8、若正六棱柱底面边长为1,高为,则直线和EF所成的角大小为( )
A. B. C. D.
二、多项选择题
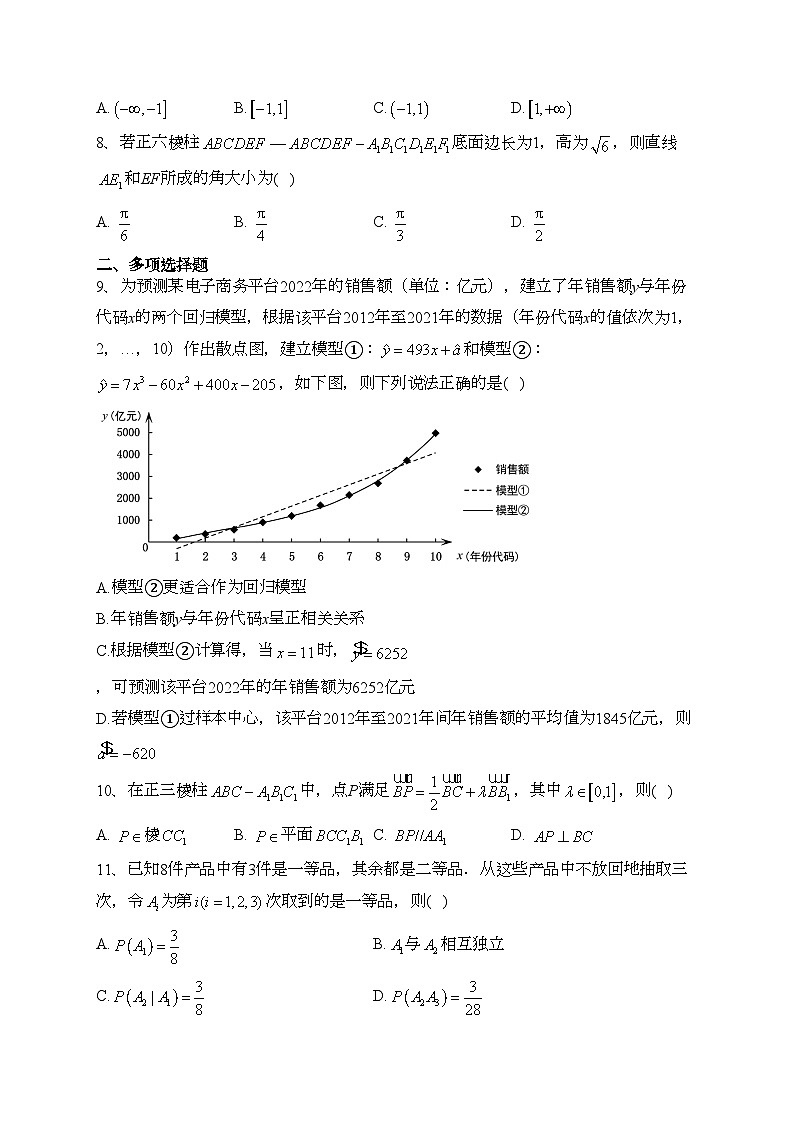
9、为预测某电子商务平台2022年的销售额(单位:亿元),建立了年销售额y与年份代码x的两个回归模型,根据该平台2012年至2021年的数据(年份代码x的值依次为1,2,…,10)作出散点图,建立模型①:和模型②:,如下图,则下列说法正确的是( )
A.模型②更适合作为回归模型
B.年销售额y与年份代码x呈正相关关系
C.根据模型②计算得,当时,,可预测该平台2022年的年销售额为6252亿元
D.若模型①过样本中心,该平台2012年至2021年间年销售额的平均值为1845亿元,则
10、在正三棱柱中,点P满足,其中,则( )
A. 棱 B. 平面 C. D.
11、已知8件产品中有3件是一等品,其余都是二等品.从这些产品中不放回地抽取三次,令为第次取到的是一等品,则( )
A. B.与相互独立
C. D.
12、已知函数,则下列说法正确的有( )
A.无最大值 B.有唯一零点
C.在单调递增 D.为的一个极小值
三、填空题
13、曲线在处的切线方程为___________.
14、已知随机变量服从标准正态分布,,则___.
15、将4个1和2个0随机排成一行代码,则代码是“101101”的概率为__________.
16、如图,在边长为2的正方体中,E,F,O分别为正方形,,ABCD的中心,点P在正方形ABCD内(含边界)运动,若直线与平面DEF无交点,则点P所形成的轨迹___点O(填“经过”或“不经过”);该轨迹长度为__________.
四、解答题
17、如图,在空间四边形ABCD中,DA,DB,DC两两垂直,,,点E在边DA上,且,F为BC的中点.
(1)用向量,,表示向量;
(2)求.
18、已知函数.
(1)求的单调区间;
(2)求在区间的最值.
19、中学生应主动承担一定的烹饪、家庭清洁、家居美化等日常生活劳动,某劳动实践基地为了解中学生对提高烹饪技术是否有兴趣,从某中学随机抽取男、女各50人进行调查.
| 有兴趣 | 没有兴趣 | 合计 |
男 | 25 |
| 50 |
女 |
|
| 50 |
合计 | 60 |
|
|
(1)请完成列联表,并判断是否有95%的把握认为对提高烹饪技术是否有兴趣与性别有关?
(2)该基地为参与调查的同学组织了一次抽奖活动.袋中装有6个除颜色外其余均相同的小球,其中4个红球、2个黄球.抽奖者从中一次抽出3个小球,抽到3个红球获得售价为88元的冰墩墩摆件;否则获得售价为3元的小礼品,设一位抽奖者获得奖品售价为X元,求.
附:,其中.
0.100 | 0.050 | 0.025 | 0010 | 0.001 | |
2.706 | 3841 | 5.024 | 6635 | 10.828 |
20、如图,在四棱锥中,底面ABCD且,,,,点M为棱PC的中点.
(1)证明:;
(2)求平面ABM与平面ABCD所成角的余弦值.
21、国家射击队队员甲、乙两人在莆田市体育训练基地射击馆进行一次队内比赛,约定赛制如下:先进行一轮25发子弹,每枪一发的常规赛,命中数多者为胜者.如果常规赛命中数相同,则进行附加赛,即每人各射击一发子弹,一人子弹命中目标而另一人子弹未命中,命中者获胜,否则每人继续射击一发,直到分出胜负为止,设甲、乙两人每发子弹命中目标的概率分别为0.9和0.8,且每发子弹是否命中目标互不影响.
(1)用X表示常规赛中甲的命中数,求和;
(2)若甲、乙两人常规赛命中数相同,求在附加赛中两人恰好各射击三发子弹甲才获胜概率.(结果保留3位小数)
参考数据:.
22、已知函数.
(1)若是的极值点,求a;
(2)当时,证明:.
参考答案
1、答案: A
解析:由与互相垂直,则,解得
故选:A
2、答案: C
解析:两人投中的概率都是0.6,根据相互独立事件的乘法公式即可得两人都投中的概率为,
故选:C
3、答案: B
解析:由得.
故选:B.
4、答案: C
解析:由导函数图像可知:当时,,函数单调递减
的单调递减区间是
故选:C
5、答案: D
解析:设,
因为与的中点相同,所以,,
解得,,所以.
故选:D.
6、答案: B
解析:李明上学骑单车准时到校的概率为,乘坐公共汽车准时到校的概率为,因此李明准时到校的概率为:,
故选:B
7、答案: A
解析:,由函数为增函数
所以恒成立,即
由,所以
故选:A
8、答案: C
解析:由题意,平移到,则为所求.
由于 ,,
故选:C.
9、答案: ABC
解析:由散点图可知年销售额y与年份代码x呈正相关关系;模型②更适合作为回归模型,故选项A,B正确.
当时,
当时,对应的年份为2022,可预测该平台2022年的年销售额为6252亿元,故选项C正确.
,解得,故选项D不正确.
故选:ABC
10、答案: BD
解析:由,
得,,共面,
又三个向量共起点,所以B,P,C,共面,
所以平面,故B正确;
则,
得,
得,
设BC得中点为O,
则,所以,
因为,所以,
即P在BC的中垂线上,故棱,故A错误;
则,
又,所以BP,不平行,故C错误;
连接OA,则,
又,OP,平面AOP,
所以平面AOP,
又平面AOP,
所以,故D正确.
故选:BD.
11、答案: AD
解析:依题意,故A正确;
,所以,故C错误
,因为,故与不独立,故B错误;
对于D:,故D正确;
故选:AD
12、答案: ACD
解析:,记
因为,且,在区间上显然递增,
所以记为的零点,则有
所以当时,,在上单调递增,
又因为,所以当时,,当时,,
所以当时,有极小值,D正确;
由上可知,在上单调递增,且当x趋近于正无穷时,也趋于正无穷,故AC正确;
易知,故B错误
故选:ACD
13、答案:
解析:因为,所以所求切线斜率,
又当时,,所以切线方程为.
故答案为:
14、答案: 0.1587
解析:随机变量服从标准正态分布,所以,
所以.
故答案为:.
15、答案:
解析:6个位置选两个位置放0,其余四个位置放1,总的排放方式共有,代码是“101101”只是15种排放方式中的一种,故概率为,
故答案为:
16、答案: ①.经过 ②
解析:因为直线与平面DEF无交点,
所以∥平面DEF,
所以需要在平面ABCD上找一点,设为Q,使平面∥平面DEF,
延长,,,分别到,,,使,,,
取正方形的中心G,的中点H,连接HG,,交平面ABCD于Q,
因为在正方体中,F,O分别为正方形,ABCD的中心,
所以,,所以四边形为平行四边形,
所以,
因为,,
所以四边形EGOF平行四边形,所以,
因为,平面DEF,DF,平面DEF,
所以平面DEF,平面DEF,
因,平面,,
平面平面DEF,
因为平面,所以平面DEF,
延长QO交CD于T,则QT为点P所形成的轨迹,
所以点P所形成的轨迹经过点O,
过G作于H,过O作于S,则
,所以,
所以,得,
所以,
所以,
故答案为:经过,
17、答案: (1)
(2)
解析:(1)依题意,得,
因为点E满足,F为BC的中点,
所以.
所以
(2)因为DA,DB,DC两两垂直.,
所以,
由(1)可得
所以
18、答案:(1) 单调递增区间为和,单调递减区间为
(2) 最大值为65,最小值为-16
解析:(1)由题意可得定义域为R,
,
令,得或.
列表如下:
x | -2 | 2 | |||
+ | 0 | - | 0 | + | |
递增↗ | 极大值16 | 递减 | 极小值-16 | 递增↗ |
所以单调递增区间为和,单调递减区间为.
(2)由(1)知在[-3,-2],单调递增,在单调递减,
又因为,,,.
所以在区间上的最大值为65,最小值为-16.
19、答案: (1) 有的把握认为对提高烹饪水平是否有兴趣与性别有关
(2)20
解析:(1)提出统计假设:对提高烹饪技术有兴趣与性别无关.
由题意,可得如下列联表:
| 有兴趣 | 没有兴趣 | 合计 |
男 | 25 | 25 | 50 |
女 | 35 | 15 | 50 |
合计 | 60 | 40 | 100 |
所以,
所以有的把握认为对提高烹饪水平是否有兴趣与性别有关.
(2)依题意X的可能取值为88,3,
所以;,
所以.
20、答案: (1)见解析
(2)
解析:(1)因为,所以.
如图,以A为原点,分别以,为x轴,y轴的正方向,过点A作,则平面xOy,以为z轴建立空间直角坐标系,
则,,,,,
因为点M为棱PC的中点,所以.
于是,
所以.
所以,即.
(2)由(1)得,
设是平面MAB的法向量,则,即
取,得,则是平面MAB的一个法向量.
又因为平面ABCD,所以是平面ABCD的一个法向量.
设平面ABM与平面ABCD所成的角为,
则,
所以平面ABM与平面ABCD所成角的余弦值为
21、答案: (1)0.272
(2)0.099
解析:(1)由题意得
所以
,
所以
(2)用A表示在附加赛中两人恰好各射击三发子弹甲才获胜,用表示在附加赛中两人各射击第一发子弹未分出胜负,用表示第二发子弹未分出胜负,用表示甲第三发子弹命中目标且乙第三发子弹未命中目标,则,且,,相互独立.
所以.
所以
解法二:
(1)同解法一;
(2)用A表示在附加赛中两人恰好各射击三发子弹甲才获胜,分以下4种情况:
①用表示在附加赛中两人各自第一发和第二发子弹都命中目标,甲第三发子弹命中目标且乙第三发子弹未命中目标,则;
②用表示在附加赛中两人各自第一发子弹均命中目标,第二发子弹均未命中目标,甲第三发子弹命中目标且乙第三发子弹未命中目标,则
;
③用表示在附加赛中两人各自第一发子弹均未命中目标,第二发子弹均命中目标,甲第三发子弹命中目标且乙第三发子弹未命中目标,则;
④用表示在附加赛中两人各自第一发和第二发子弹都未命中目标,甲第三发子弹命中目标且乙第三发子弹未命中目标,则
因为,且,、、两两互斥,
所以
22、答案: (1)
(2)见解析
解析:(1)依题意,的定义域为,
由,得,
因为是的极值点,所以,即,即
当1时,,
当时,,所以在单调递增;
当时,,所以在单调递减;
所以在处取得极大值,符合题意
因此
(2)当时,要证,只需证,
即证,等价于证明
令,则
令,则,所以对恒成立,
故 在 单调递减,
又,所以,
所以在上恰有一个零点,且.
当时,,即,所以在单调递增;
当时,,即,所以在单调递减,
所以.
又因为,即,即,即,即,
所以
所以,
又因为,所以,即,
因此,即,圆
2022-2023学年福建省莆田市高二下学期期末质量监测数学试题(含解析): 这是一份2022-2023学年福建省莆田市高二下学期期末质量监测数学试题(含解析),共20页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年福建省莆田市高二下学期期末质量监测数学试题含答案: 这是一份2022-2023学年福建省莆田市高二下学期期末质量监测数学试题含答案,共20页。试卷主要包含了单选题,多选题,填空题,双空题,解答题等内容,欢迎下载使用。
福建省莆田市2022-2023学年高二数学下学期期末质量监测试题(Word版附解析): 这是一份福建省莆田市2022-2023学年高二数学下学期期末质量监测试题(Word版附解析),共22页。试卷主要包含了 设,,,则, 某学习小组收集了7组样本数据等内容,欢迎下载使用。












