2022北京一六一中初三（上）期中数学

这是一份2022北京一六一中初三（上）期中数学，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
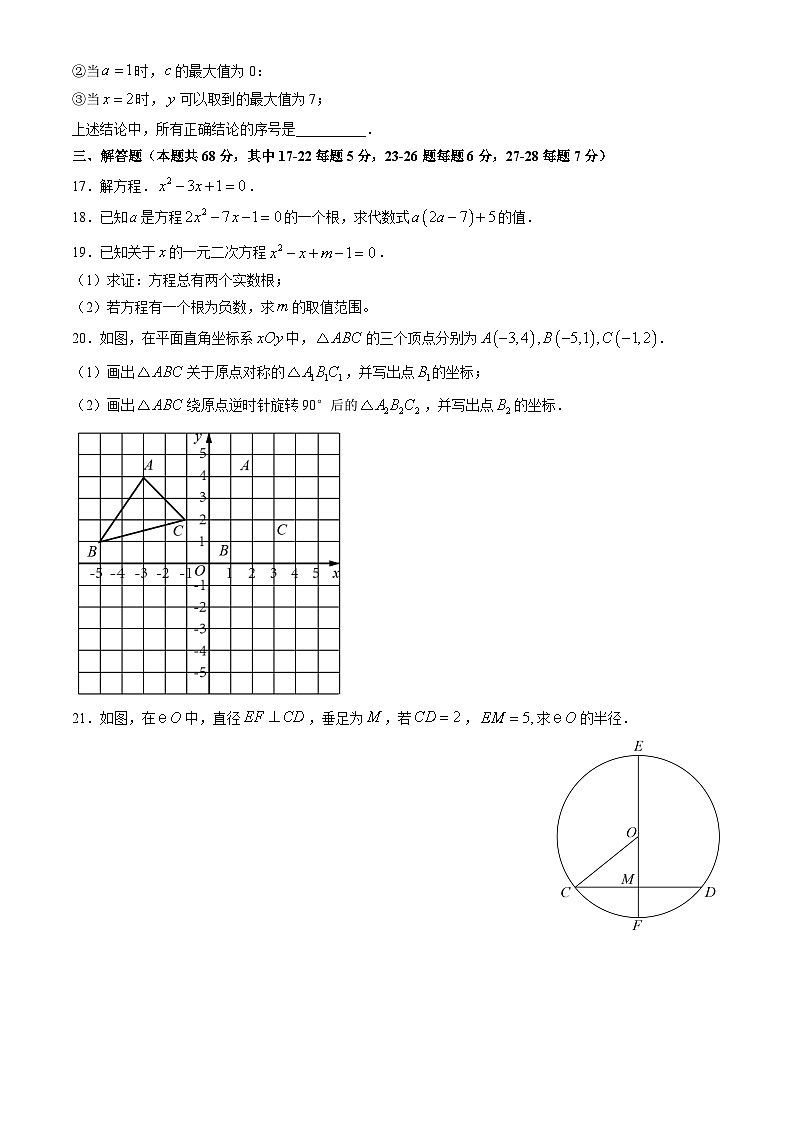
2022北京一六一中初三（上）期中数    学2022年11月班级　　         　姓名　　           学号　　         考生须知1．本试卷共4页，满分100分，考试时间120分钟。2．试卷答案一律填涂或书写在答题卡上，在试卷上作答无效。3．答题卡上选择题用2B铅笔作答，其他题用黑色字迹钢笔或签字笔作答。4．考试结束后，将答题卡交回。一、选择题（本题共16分，每小题2分）1．下列图形中，既是轴对称图形又是中心对称图形的是（    ）A． B． C． D．2．抛物线的顶点坐标为（    ）A． B． C． D．3．将一元二次方程通过配方转化为的形式，下列结果中正确的是（    ）A． B． C． D．4．如图，，，，绕点顺时针旋转到的位置，使得点在同一条直线上，那么旋转角等于（    ）A．55° B．70°C．125° D．145°5．如图，为的直径，点在上，若，则的度数为（    ）A．60° B．45° C．30° D．15°6．已知点A、均在抛物线上，则下列结论正确的是（    ）A． B． C． D．7．已知函数，其中， ，此函数的图象可以是（    ）A                 B                   C                  D8．如图，抛物线的对称轴为直线，如果关于的方程的一个根为4，那么该方程的另一个根为（    ）A． B． C．1 D．3二、填空题（本题共16分，每小题2分）9．若关于的一元二次方程的一根为1，则的值是__________．10．请写出一个开口向下，并且与轴交于点的抛物线的表达式：__________．11．某公司8月份销售额为200万元，10月份销售额为320万元，求销售额平均每月的增长率，设销售额平均每月的增长率为，则可列方程为_________________________．12．如图，点A在上，弦垂直且平分，垂足为．若半径，则的长为__________．13．将抛物线向上平移个单位长度后，所得新抛物线经过点，则的值为__________．14．如图，将绕点顺时针旋转30°得到，点的对应点恰好落在边上，则__________．15．已知抛物线与直线相交于两点，若点的横坐标，则点的横坐标，的值为__________．16．已知二次函数，当时，总有，有如下几个结论：①当时， ，②当时，的最大值为0：③当时，可以取到的最大值为7；上述结论中，所有正确结论的序号是__________．三、解答题（本题共68分，其中17-22每题5分，23-26题每题6分，27-28每题7分）17．解方程．．18．已知是方程的一个根，求代数式的值．19．已知关于的一元二次方程．（1）求证：方程总有两个实数根；（2）若方程有一个根为负数，求的取值范围。20．如图，在平面直角坐标系中，的三个顶点分别为．（1）画出关于原点对称的，并写出点的坐标；（2）画出绕原点逆时针旋转90°后的，并写出点的坐标．21．如图，在中，直径，垂足为，若，求的半径．
22．已知二次函数．（1）直接写出二次函数图象的顶点坐标________________；（2）画出这个二次函数的图象________________．（3）当0<x<4时，y的取值范围是_______________．23．如图，在中， ， ，是边上一点（点与，不重合），连结，将线段绕点逆时针旋转90°得到线段，连结交于点，连接．（1）求证：； （2）当时，求的度数．  24．已知：二次函数的图象与轴交于，两点，其中点坐标为，与轴交于点，点在抛物线上．（1）求抛物线的解析式；（2）若抛物线上有一动点，使三角形的面积为6，求点坐标。
25．某景观公园内人工湖里有一组小型喷泉，水柱从垂直于湖面的水枪喷出，水柱落于湖面的路径形状是抛物线。现测量出如下数据，在距水枪水平距离为米的地点，水柱距离湖面高度为米．（米）0.01.02.03.04.8…（米）1.01.752.01.750.04…请解决以下问题：（1）在网格中建立适当的平面直角坐标系，根据已知数据描点，并用平滑的曲线连接。（2）请结合表中所给数据或所画图象，写出水柱最高点距离湖面的高度为_________米，此时抛物线的解析式为__________________________．（3）现公园想通过喷泉设立新的游玩项目，准备通过调节水枪高度，使得公园湖中的4人平顶游船能从喷泉下方通过。已知游船宽度为1.6米，顶棚到水面的高度为2米。要求游船从喷泉水柱中间通过时，为避免游船被喷泉淋到，顶棚到水柱的垂直距离均不小于0.5米，求公园应该将水枪高度调节到多少米以上？（备注：水枪调节过程中所喷出的抛物线的形状相同）    26．在平面直角坐标系中，抛物线经过点，．（1）直接写出的值和此抛物线的对称轴；（2）若此抛物线与直线没有公共点，求的取值范围；（3）点，在此抛物线上，且当时，都有，直接写出的取值范围． 
27．在中， ，．点是内动点，连接， ，将绕点顺时针旋转，使边与重合，得到，延长与射线交于点 （点与点不重合）。（1）依题意补全图1；（2）探究与的数量关系为_________________________．（3）如图2，若平分，用等式表示线段，，之间的数量关系，并证明。28．对于平面直角坐标系中第一象限内的点和图形，给出如下定义：过点作轴和轴的垂线，垂足分别为，若图形中的任意一点满足且，则称四边形是图形的一个覆盖，点为这个覆盖的一个特征点．例：已知，，则点为线段的一个覆盖的特征点（1）已知点，①在， ，中，是的覆盖特征点的为___________；②若在一次函数的图象上存在的覆盖的特征点，求的取值范围。（2）以点为圆心，半径为1作圆，在抛物线上存在的覆盖的特征点，直接写出的取值范围___________．