2018北京育英中学四年制初一（上）期中数学（教师版）

2018北京育英中学四年制初一（上）期中

数    学

2018.11.4

一、选择题（每题3分，共24分）

1．（3分）的相反数是（　　）

A．﹣ B．3 C．﹣3 D．

2．（3分）绝对值等于2的数是（　　）

A．2 B．﹣2 C．2或﹣2 D．

3．（3分）计算的正确结果是（　　）

A． B． C．1 D．﹣1

4．（3分）与﹣π的大小关系是（　　）

A． B． C． D．无法确定

5．（3分）有理数a，b在数轴上的位置如图所示，则下列结论中，错误的是（　　）

A．a＜0＜b B．|a|＞|b| C．﹣a＞b D．b﹣a＜a+b

6．（3分）若|x﹣2|和|y+3|互为相反数，则x﹣y的值是（　　）

A．5 B．﹣5 C．1 D．﹣1

7．（3分）下列各组比中，与3：4能组成比例的是（　　）

A．4：3 B．0.8：0.6 C． D．15：20

8．（3分）若a＜﹣3，则|﹣3﹣a|﹣|a﹣4|化简后等于（　　）

A．1﹣2a B．﹣7 C．1 D．7

二、填空题（每题3分，共24分）

9．（3分）甲潜水员所在高度为﹣45米，乙潜水员在甲的上方15米处，则乙潜水员的所在的高度是　     　．

10．（3分）比较大小：﹣（﹣4.2）　 　|﹣5|．（填“＞，＜”）

11．（3分）若|x﹣3|＝2，则x的值为　    　．

12．（3分）在一幅比例尺是1：3000000的地图上，量得甲、乙两地的距离是30厘米，如果在另幅图上，甲、乙两地的距离是20厘米，另一幅地图的比例尺是 　         　．

13．（3分）数轴上的点A表示﹣3，将点A先向右移动7个单位长度，再向左移动5个单位长度，那么此时的点A到原点的距离是　 　个单位长度．

14．（3分）希望小学校舍建设用去40万元，比计划少用10万元，节约了 　   　%．

15．（3分）一件衣服进价500元，商场加价60%出售发现销量不好后，决定再打7折出售，那么每件衣服会 　   　（填“亏损，盈利”） 　   　元．

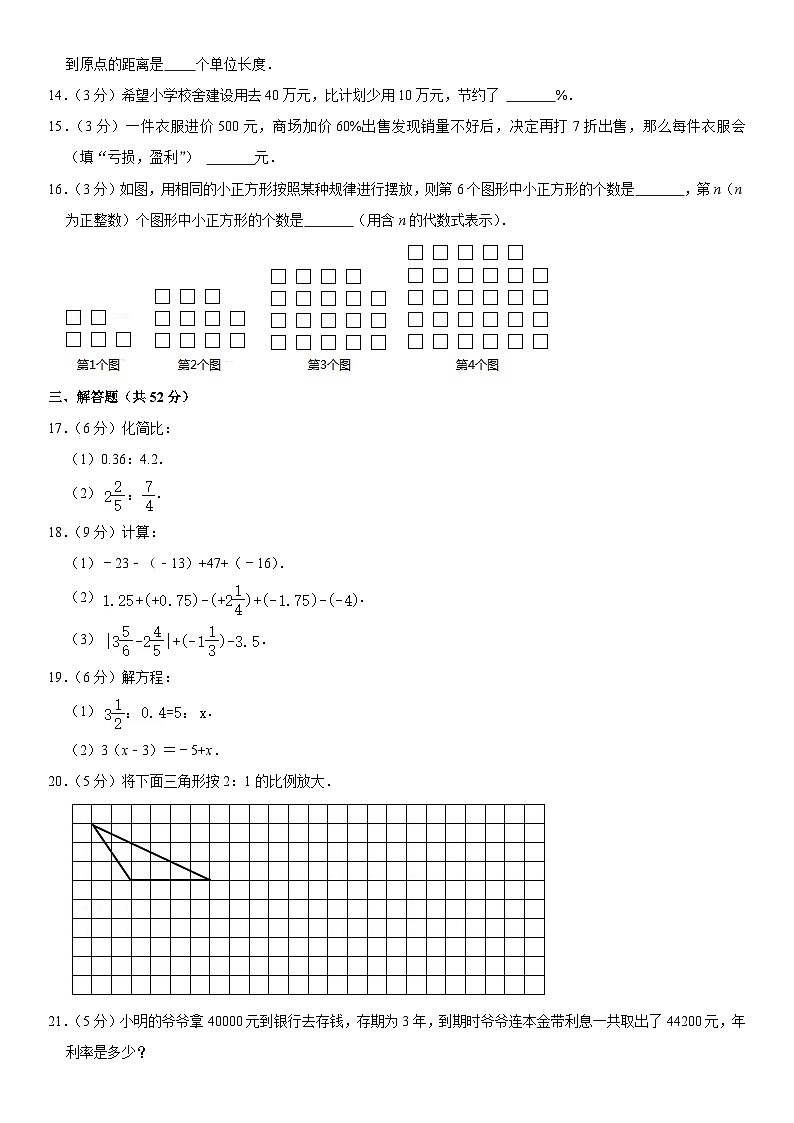
16．（3分）如图，用相同的小正方形按照某种规律进行摆放，则第6个图形中小正方形的个数是　   　，第n（n为正整数）个图形中小正方形的个数是　   　（用含n的代数式表示）．

三、解答题（共52分）

17．（6分）化简比：

（1）0.36：4.2．

（2）．

18．（9分）计算：

（1）﹣23﹣（﹣13）+47+（﹣16）．

（2）．

（3）．

19．（6分）解方程：

（1）．

（2）3（x﹣3）＝﹣5+x．

20．（5分）将下面三角形按2：1的比例放大．

21．（5分）小明的爷爷拿40000元到银行去存钱，存期为3年，到期时爷爷连本金带利息一共取出了44200元，年利率是多少？

22．（4分）小华看一本书，已看的页数和没看的页数之比是13：7，已看的页数比剩下的页数多90页，这本书一共有多少页？

23．（5分）画一条数轴，并把下面这些数用数轴上的点表示出来：，﹣（﹣4），﹣3，|﹣1.4|．

24．（7分）阅读下面材料：

小丁在研究数学问题时遇到一个定义：对于排好顺序的三个数：x1，x2，x3，称为数列x1，x2，x3．计算|x1|，，，将这三个数的最小值称为数列x1，x2，x3的价值．例如，对于数列2，﹣1，3，因为|2|＝2，＝，＝，所以数列2，﹣1，3的价值为．

小丁进一步发现：当改变这三个数的顺序时，所得到的数列都可以按照上述方法计算其相应的价值．如数列﹣1，2，3的价值为；数列3，﹣1，2的价值为1；…．经过研究，小丁发现，对于“2，﹣1，3”这三个数，按照不同的排列顺序得到的不同数列中，价值的最小值为．

根据以上材料，回答下列问题：

（1）数列﹣4，﹣3，2的价值为　              　；

（2）将“﹣4，﹣3，2”这三个数按照不同的顺序排列，可得到若干个数列，这些数列的价值的最小值为　              　，取得价值最小值的数列为　              　（写出一个即可）；

（3）将2，﹣9，a（a＞1）这三个数按照不同的顺序排列，可得到若干个数列．若这些数列的价值的最小值为1，则a的值为　              　．

25．（5分）已知数轴上两点A、B对应的数分别为﹣1，3，点P为数轴上一动点，其对应的数为x．

（1）若点P到点A、点B的距离相等，求点P对应的数；

（2）数轴上是否存在点P，使点P到点A、点B的距离之和为5？若存在，请求出x的值．若不存在，请说明理由？

（3）当点P以每分钟一个单位长度的速度从O点向左运动时，点A以每分钟5个单位长度向左运动，点B以每分钟20个单位长度向左运动，问它们同时出发，几分钟后P点到点A、点B的距离相等？

2018北京育英中学四年制初一（上）期中数学

参考答案

一、选择题（每题3分，共24分）

1．【分析】求一个数的相反数，即在这个数的前面加负号．

【解答】解：根据相反数的定义，得的相反数是﹣．

故选：A．

【点评】本题主要考查了相反数的求法，比较简单．

2．【分析】根据绝对值的定义进行选择即可．

【解答】解：∵|2|＝2，|﹣2|＝2，

∴绝对值等于2的数是±2，

故选：C．

【点评】本题考查了绝对值，掌握绝对值的定义是解题的关键．

3．【分析】根据有理数加法的运算方法，求出算式的正确结果是多少即可．

【解答】解：＝﹣（）＝﹣1．

故选：D．

【点评】此题主要考查了有理数的加法的运算方法，要熟练掌握，解答此题的关键是要明确：①同号相加，取相同符号，并把绝对值相加．②绝对值不等的异号加减，取绝对值较大的加数符号，并用较大的绝对值减去较小的绝对值．互为相反数的两个数相加得0．③一个数同0相加，仍得这个数．

4．【分析】先求出两数的绝对值，再根据两个负数比较大小，其绝对值大的反而小比较即可．

【解答】解：|﹣|＝≈3.142859142859，

|﹣π|＝π≈3.1415926，

∵＞π，

∴﹣＜π，

故选：C．

【点评】本题考查了实数的大小比较法则，能熟记实数的大小比较法则是解此题的关键，注意：正数都大于0，负数都小于0，正数大于一切负数，两个负数比较大小，其绝对值大的反而小．

5．【分析】根据数轴表示数的方法得到a＜0＜b，且|a|＞b，则﹣a＞b，b﹣a＞b+a．

【解答】解：∵a＜0＜b，且|a|＞b，

∴﹣a＞b，b﹣a＞b+a．

故选：D．

【点评】本题考查了有理数的大小比较：正数大于零，负数小于零；负数的绝对值越大，这个数反而越小．也考查了数轴．

6．【分析】根据相反数的概念列出算式，根据非负数的性质求出x、y，根据有理数的减法法则计算，得到答案．

【解答】解：∵|x﹣2|和|y+3|互为相反数，

∴|x﹣2|+|y+3|＝0，

∴x﹣2＝0，y+3＝0，

解得x＝2，y＝﹣3，

则x﹣y＝2﹣（﹣3）＝2+3＝5，

故选：A．

【点评】本题考查的是非负数的性质，掌握绝对值的非负性是解题的关键．

7．【分析】根据有理数的除法运算法则即可求出答案．

【解答】解：A、4：3≠3：4，故A不符合题意．

B、0.8：0.6＝4：3，故B不符合题意．

C、：＝4：3，故C不符合题意．

D、15：20＝3：4，故D符合题意．

故选：D．

【点评】本题考查有理数的除法，解题的关键是熟练运用有理数的除法运算，本题属于基础题型．

8．【分析】根据a＜﹣3，利用绝对值的性质对式子进行化简即可．

【解答】解：已知a＜﹣3，

原式＝﹣3﹣a+a﹣4＝﹣7．

故选：B．

【点评】本题考查了绝对值，利用绝对值的性质对式子化简是解题的关键．

二、填空题（每题3分，共24分）

9．【分析】根据题意只要把两数相加即可得出答案．

【解答】解：﹣45+15＝﹣30（米）．

故答案为：﹣30米

【点评】此题考查了正数与负数，要求熟练掌握有理数的加法法则．

10．【分析】根据相反数的定义以及绝对值的性质化简后再比较大小即可．

【解答】解：﹣（﹣4.2）＝4.2，|﹣5|＝5，

∴﹣（﹣4.2）＜|﹣5|，

故答案为：＜．

【点评】本题考查了有理数比较大小，正数大于零，零大于负数．两个负数比较时绝对值大的反而小．

11．【分析】由题意和绝对值的性质可得x﹣3＝±2，求x的值即可，注意不要漏解．

【解答】解：由题意得：x﹣3＝±2，

x＝2+3或x＝﹣2+3，

即x＝5或1．

故填5或1．

【点评】本题考查了一元一次方程的解法，涉及到绝对值的性质，比较简单，注意不要漏解．

12．【分析】根据“比例尺是1：300000的地图上量得甲乙两地相距30cm”，求出甲、乙两地的实际距离；再根据比例尺的意义知道，用图上距离比实际距离就是该图的比例尺．

【解答】解：甲、乙两地的实际距离：300000×30＝9000000（cm），

另一幅地图的比例尺是：20：9000000＝1：450000；

故答案为：1：450000．

【点评】解答此题的关键是根据甲、乙两地的实际距离不变，再根据比例尺、图上距离与实际距离的关系，解决问题．

13．【分析】本题可根据数轴上点的移动和数的大小变化规律，左减右加来计算．

【解答】解：依题意得该数为：﹣3+7﹣5＝﹣1．

∵﹣1到原点的距离为：1个单位长度．

∴此时的点A到原点的距离是1个单位长度．

故答案为1．

【点评】此题考查了数轴的有关知识，正负数在实际问题中，可以表示具有相反意义的量．本题中，向左、向右具有相反意义，可以用正负数来表示，从而列出算式求解．

14．【分析】根据题意列出算式，计算即可求出值．

【解答】解：根据题意得：10÷（40+10）×100%＝20%，

所以，节约了20%．

故答案为：20．

【点评】此题考查了有理数的混合运算，列出正确的算式是解本题的关键．

15．【分析】根据题意列出算式，计算即可作出判断．

【解答】解：根据题意得：500×（1+60%）×70%＝500×1.6×0.7＝560（元），

560﹣500＝60（元），

则每件衣服会盈利60元．

故答案为：盈利，60．

【点评】此题考查了有理数的混合运算，列出正确的算式是解本题的关键．

16．【分析】观察图形可知，第1个图形共有小正方形的个数为2×2+1；第2个图形共有小正方形的个数为3×3+2；第3个图形共有小正方形的个数为4×4+3；…；则第n个图形共有小正方形的个数为（n+1）2+n，进而得出答案．

【解答】解：第1个图形共有小正方形的个数为2×2+1；

第2个图形共有小正方形的个数为3×3+2；

第3个图形共有小正方形的个数为4×4+3；

…；

则第n个图形共有小正方形的个数为（n+1）2+n，

所以第6个图形共有小正方形的个数为：7×7+6＝55．

故答案为：55；（n+1）2+n

【点评】本题考查了规律型：图形的变化类，解决这类问题首先要从简单图形入手，抓住随着“编号”或“序号”增加时，后一个图形与前一个图形相比，在数量上增加（或倍数）情况的变化，找出数量上的变化规律，从而推出一般性的结论．

三、解答题（共52分）

17．【分析】根据有理数的除法运算法则即可求出答案．

【解答】解：（1）0.36：4.2＝3：35．

（2）2：＝48：35．

【点评】本题考查有理数的除法，解题的关键是熟练运用有理数的除法运算，本题属于基础题型．

18．【分析】（1）根据有理数的加减运算法则即可求出答案．

（2）根据有理数的加减运算法则即可求出答案．

（3）根据有理数的加减运算法则以及绝对值的性质即可求出答案．

【解答】解：（1）原式＝﹣23+13+47﹣16

＝﹣10+47﹣16

＝﹣37﹣16

＝﹣53．

（2）原式＝+﹣﹣+4

＝﹣﹣+4

＝﹣+4

＝﹣2+4

＝2．

（3）原式＝|﹣|﹣﹣

＝﹣﹣

＝．

【点评】本题考查有理数的加减，解题的关键是熟练运用有理数的加减法运算，本题属于基础题型．

19．【分析】（1）由比例的性质化为乘积式可得2＝x，求解即可；

（2）先去括号，再移项、合并同类项，即可求解．

【解答】解：（1），

化为：5×0.4＝x，

可得2＝x，

解得x＝；

（2）3（x﹣3）＝﹣5+x，

去括号得，3x﹣9＝﹣5+x，

移项、合并同类项，得2x＝4，

解得x＝2．

【点评】本题考查一元一次方程的解，熟练掌握一元一次方程的解法是解题的关键．

20．【分析】以A为位似中心，作出△CDE，使得△CDE∽△CBA且相似比为2．

【解答】解：如图，△CDE即为所求．

【点评】本题考查作图﹣位似变换，解题的关键是掌握位似变换的性质，正确作出图形．

21．【分析】本题中，本金是40000元，时间是3年，本金和利息共44200元，根据关系式：本息＝本金+本金×利率×时间，推出：（本息﹣本金）÷本金÷时间，解决问题．

【解答】解：设年利率是x，根据题意得：

44200＝40000x×3+40000，

解得：x＝3.5%，

答：年利率是3.5%．

【点评】此题考查一元一次方程的应用，属于利息问题，灵活运用关系式：本息＝本金+本金×利率×时间，进行解答．

22．【分析】先设这本书一共有x页，然后根据已看的页数和没看的页数之比是13：7，已看的页数比剩下的页数多90页，可以列出相应的方程，然后求解即可．

【解答】解：设这本书一共有x页，

由题意可得，﹣x＝90，

解得x＝300，

答：这本书一共有300页．

【点评】本题考查一元一次方程的应用，解答本题的关键是明确题意，找出等量关系，列出相应的方程．

23．【分析】先化简相反数，绝对值，然后利用数轴表示各数．

【解答】解：∵2＝，﹣（﹣4）＝4，|﹣1.4|＝1.4，

∴它们在数轴上的位置如下：

【点评】本题主要考查绝对值，相反数，利用数轴表示数，理解绝对值和相反数的概念，利用数形结合思想在数轴上准确表示各数是解题关键．

24．【分析】（1）根据上述材料给出的方法计算其相应的价值即可；

（2）按照三个数不同的顺序排列算出价值，由计算可以看出，要求得这些数列的价值的最小值；只有当前两个数的和的绝对值最小，最小只能为|﹣3+2|＝1，由此得出答案即可；

（3）分情况算出对应的数值，建立方程求得a的数值即可．

【解答】解：（1）因为|﹣4|＝4，||＝3.5，||＝，

所以数列﹣4，﹣3，2的价值为．

（2）数列的价值的最小值为||＝，

数列可以为：﹣3，2，﹣4，；或2，﹣3，﹣4．

（3）当||＝1，则a＝0，不合题意；

当||＝1，则a＝11或7（舍弃）；

当||＝1，则a＝4或10（舍弃）．

∴a＝11或4．

故答案为：；，﹣3，2，﹣4，；或2，﹣3，﹣4；11或4．

【点评】此题考查数字的变化规律，理解运算的方法是解决问题的关键．

25．【分析】（1）根据点P到点A、点B的距离相等，结合数轴可得答案；

（2）此题要分两种情况：①当P在AB左侧时，②当P在AB右侧时，然后再列出方程求解即可；

（3）点P、点A、点B同时向左运动，点B的运动速度最快，点P的运动速度最慢．故P点总位于A点右侧，B可能追上并超过A．P到A、B的距离相等，应分两种情况讨论．

【解答】解：（1）如图，若点P到点A、点B的距离相等，P为AB的中点，BP＝PA．

依题意得3﹣x＝x﹣（﹣1），

解得x＝1；

（2）由AB＝4，若存在点P到点A、点B的距离之和为5，P不可能在线段AB上，只能在A点左侧，或B点右侧．

①P在点A左侧，PA＝﹣1﹣x，PB＝3﹣x，

依题意得（﹣1﹣x）+（3﹣x）＝5，

解得  x＝﹣1.5；

②P在点B右侧，PA＝x﹣（﹣1）＝x+1，PB＝x﹣3，

依题意得（x+1）+（x﹣3）＝5，

解得x＝3.5；

（3）设运动t分钟，此时P对应的数为﹣t，B对应的数为3﹣20t，A对应的数为﹣1﹣5t．

①B未追上A时，PA＝PB，则P为AB中点．B在P的右侧，A在P的左侧．

PA＝﹣t﹣（﹣1﹣5t）＝1+4t，PB＝3﹣20t﹣（﹣t）＝3﹣19t，

依题意有1+4t＝3﹣19t，

解得 t＝；

②B追上A时，A、B重合，此时PA＝PB．A、B表示同一个数．

依题意有﹣1﹣5t＝3﹣20t，

解得t＝．

即运动或分钟时，P到A、B的距离相等．

【点评】此题主要考查了一元一次方程的应用，以及数轴，关键是理解题意，表示出两点之间的距离，利用数形结合法列出方程．