四川省攀枝花市2018年中考数学试卷【含答案】

四川省攀枝花市2018年中考数学试卷

一、选择题：

1．下列实数中，无理数是（　　）

A．0 B．﹣2 C． D．

2．下列运算结果是a5的是（　　）

A．a10÷a2 B．（a2）3 C．（﹣a）5 D．a3•a2

3．如图，实数﹣3、x、3、y在数轴上的对应点分别为M、N、P、Q，这四个数中绝对值最小的数对应的点是（　　）

A．点M B．点N C．点P D．点Q

4．如图，等腰直角三角形的顶点A，C分别在直线a、b上，若a∥b，∠1=30°，则∠2的度数为（　　）

A．30° B．15° C．10° D．20°

5．下列平面图形中，既是中心对称图形，又是轴对称图形的是（　　）

A．菱形 B．等边三角形 C．平行四边形 D．等腰梯形

6．抛物线y=x2﹣2x+2的顶点坐标为（　　）

A．（1，1） B．（﹣1，1） C．（1，3） D．（﹣1，3）

7．若点A（a+1，b﹣2）在第二象限，则点B（﹣a，1﹣b）在（　　）

A．第一象限 B．第二象限 C．第三象限 D．第四象限

8．布袋中装有除颜色外没有其他区别的1个红球和2个白球，搅匀后从中摸出一个球，放回搅匀，再摸出第二个球，两次都摸出白球的概率是（　　）

A． B． C． D．

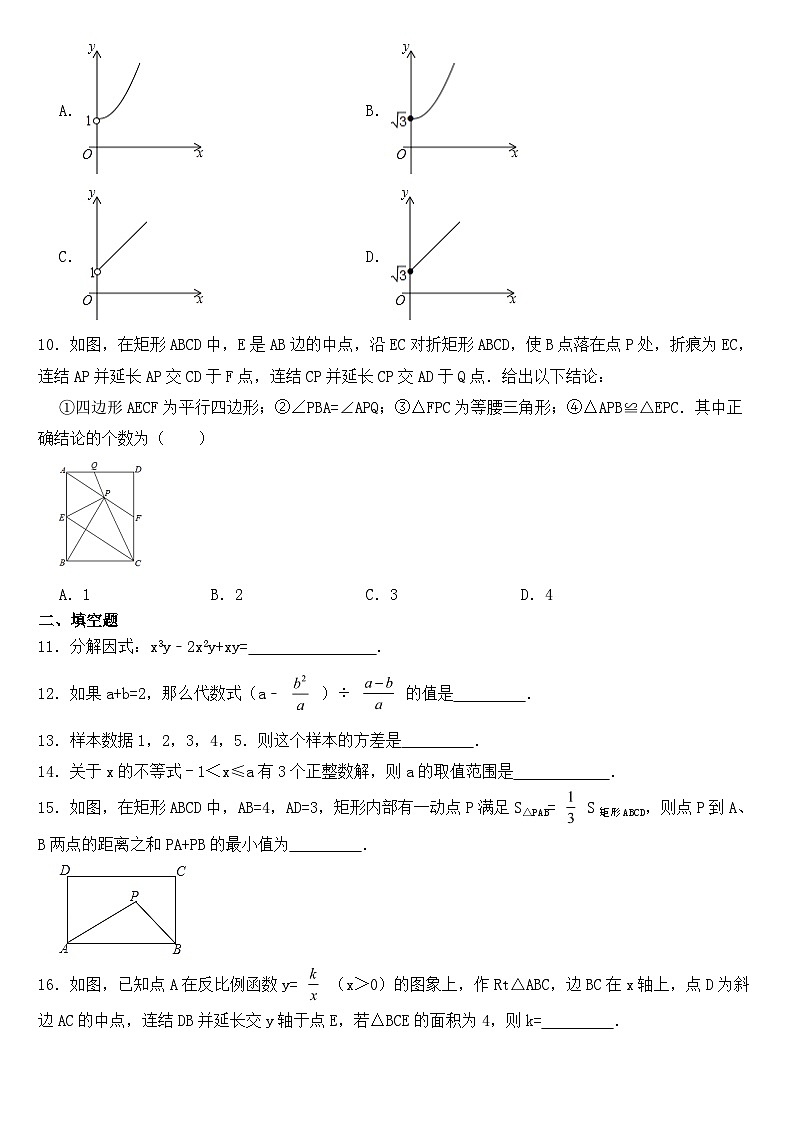
9．如图，点A的坐标为（0，1），点B是x轴正半轴上的一动点，以AB为边作Rt△ABC，使∠BAC=90°，∠ACB=30°，设点B的横坐标为x，点C的纵坐标为y，能表示y与x的函数关系的图象大致是（　　）

A． B．

C． D．

10．如图，在矩形ABCD中，E是AB边的中点，沿EC对折矩形ABCD，使B点落在点P处，折痕为EC，连结AP并延长AP交CD于F点，连结CP并延长CP交AD于Q点．给出以下结论：

①四边形AECF为平行四边形；②∠PBA=∠APQ；③△FPC为等腰三角形；④△APB≌△EPC．其中正确结论的个数为（　　）

A．1 B．2 C．3 D．4

二、填空题

11．分解因式：x3y﹣2x2y+xy=　            　．

12．如果a+b=2，那么代数式（a﹣ ）÷ 的值是　     　．

13．样本数据1，2，3，4，5．则这个样本的方差是　     　．

14．关于x的不等式﹣1＜x≤a有3个正整数解，则a的取值范围是　        　．

15．如图，在矩形ABCD中，AB=4，AD=3，矩形内部有一动点P满足S△PAB= S矩形ABCD，则点P到A、B两点的距离之和PA+PB的最小值为　     　．

16．如图，已知点A在反比例函数y= （x＞0）的图象上，作Rt△ABC，边BC在x轴上，点D为斜边AC的中点，连结DB并延长交y轴于点E，若△BCE的面积为4，则k=　     　．

三、解答题

17．解方程： =1．

18．某校为了预测本校九年级男生毕业体育测试达标情况，随机抽取该年级部分男生进行了一次测试（满分50分，成绩均记为整数分），并按测试成绩m（单位：分）分成四类：A类（45＜m≤50），B类（40＜m≤45），C类（35＜m≤40），D类（m≤35）绘制出如图所示的两幅不完整的统计图，请根据图中信息解答下列问题：

（1）求本次抽取的样本容量和扇形统计图中A类所对的圆心角的度数；

（2）若该校九年级男生有500名，D类为测试成绩不达标，请估计该校九年级男生毕业体育测试成绩能达标的有多少名？

19．攀枝花市出租车的收费标准是：起步价5元（即行驶距离不超过2千米都需付5元车费），超过2千米以后，每增加1千米，加收1.8元（不足1千米按1千米计）．某同学从家乘出租车到学校，付了车费24.8元．求该同学的家到学校的距离在什么范围？

20．已知△ABC中，∠A=90°．

（1）请在图1中作出BC边上的中线（保留作图痕迹，不写作法）；

（2）如图2，设BC边上的中线为AD，求证：BC=2AD．

21．如图，在平面直角坐标系中，A点的坐标为（a，6），AB⊥x轴于点B，cos∠OAB═ ，反比例函数y= 的图象的一支分别交AO、AB于点C、D．延长AO交反比例函数的图象的另一支于点E．已知点D的纵坐标为 ．

（1）求反比例函数的解析式；（2）求直线EB的解析式；（3）求S△OEB．

22．如图，在△ABC中，AB=AC，以AB为直径的⊙O分别与BC、AC交于点D、E，过点D作DF⊥AC于点F．

（1）若⊙O的半径为3，∠CDF=15°，求阴影部分的面积；

（2）求证：DF是⊙O的切线；

（3）求证：∠EDF=∠DAC．

23．如图，在△ABC中，AB=7.5，AC=9，S△ABC= ．动点P从A点出发，沿AB方向以每秒5个单位长度的速度向B点匀速运动，动点Q从C点同时出发，以相同的速度沿CA方向向A点匀速运动，当点P运动到B点时，P、Q两点同时停止运动，以PQ为边作正△PQM（P、Q、M按逆时针排序），以QC为边在AC上方作正△QCN，设点P运动时间为t秒．

（1）求cosA的值；

（2）当△PQM与△QCN的面积满足S△PQM= S△QCN时，求t的值；

（3）当t为何值时，△PQM的某个顶点（Q点除外）落在△QCN的边上．

24．如图，对称轴为直线x=1的抛物线y=x2﹣bx+c与x轴交于A（x1，0）、B（x2，0）（x1＜x2）两点，与y轴交于C点，且 ﹣ ．

（1）求抛物线的解析式；

（2）抛物线顶点为D，直线BD交y轴于E点；

①设点P为线段BD上一点（点P不与B、D两点重合），过点P作x轴的垂线与抛物线交于点F，求△BDF面积的最大值；

②在线段BD上是否存在点Q，使得∠BDC=∠QCE？若存在，求出点Q的坐标；若不存在，请说明理由．

1．C

2．D

3．B

4．B

5．A

6．A

7．D

8．A

9．C

10．B

11．xy（x﹣1）2

12．2

13．2

14．3≤a＜4

15．4

16．8

17．解：去分母得：3（x﹣3）﹣2（2x+1）=6，去括号得：3x﹣9﹣4x﹣2=6，移项得：﹣x=17，系数化为1得：x=﹣17．

18．（1）解：本次抽取的样本容量为10÷20%=50，扇形统计图中A类所对的圆心角的度数为360°×20%=72°；

（2）解：估计该校九年级男生毕业体育测试成绩能达标的有500×（1﹣ ）=470名．

19．解：设该同学的家到学校的距离是x千米，依题意：24.8﹣1.8＜5+1.8（x﹣2）≤24.8，解得：12＜x≤13．

故该同学的家到学校的距离在大于12小于等于13的范围．

20．（1）解：如图1，AD为所作；

（2）解：证明：延长AD到E，使ED=AD，连接EB、EC，如图2．∵CD=BD，AD=ED，∴四边形ABEC为平行四边形．

∵∠CAB=90°，∴四边形ABEC为矩形，∴AE=BC，∴BC=2AD．

21．（1）解：∵A点的坐标为（a，6），AB⊥x轴，∴AB=6．

∵cos∠OAB═ = ，∴ = ，∴OA=10，由勾股定理得：OB=8，∴A（8，6），∴D（8， ）．

∵点D在反比例函数的图象上，∴k=8× =12，∴反比例函数的解析式为：y= ；

（2）解：设直线OA的解析式为：y=bx．

∵A（8，6），∴8b=6，b= ，∴直线OA的解析式为：y= x，则 = x，x=±4，∴E（﹣4，﹣3），设直线BE的解式为：y=mx+n，把B（8，0），E（﹣4，﹣3）代入得： ，解得： ，∴直线BE的解析式为：y= x﹣2；

（3）解：S△OEB= OB•|yE|= ×8×3=12．

22．（1）解：连接OE，过O作OM⊥AC于M，则∠AMO=90°．∵DF⊥AC，∴∠DFC=90°．

∵∠FDC=15°，∴∠C=180°﹣90°﹣15°=75°．

∵AB=AC，∴∠ABC=∠C=75°，∴∠BAC=180°﹣∠ABC-∠C=30°，∴OM= OA= = ，AM= OM= ．

∵OA=OE，OM⊥AC，∴AE=2AM=3 ，∴∠BAC=∠AEO=30°，∴∠AOE=180°﹣30°﹣30°=120°，∴阴影部分的面积S=S扇形AOE﹣S△AOE= ；

（2）解：证明：连接OD，∵AB=AC，OB=OD，∴∠ABC=∠C，∠ABC=∠ODB，∴∠ODB=∠C，∴AC∥OD．

∵DF⊥AC，∴DF⊥OD．

∵OD过O，∴DF是⊙O的切线；

（3）解：证明：连接BE，

∵AB为⊙O的直径，∴∠AEB=90°，BE⊥AC．

∵DF⊥AC，∴BE∥DF，∴∠FDC=∠EBC．

∵∠EBC=∠DAC，∴∠FDC=∠DAC．

∵A、B、D、E四点共圆，∴∠DEF=∠ABC．

∵∠ABC=∠C，∴∠DEC=∠C．

∵DF⊥AC，∴∠EDF=∠FDC，∴∠EDF=∠DAC．

23．（1）解：如图1中，作BE⊥AC于E．

∵S△ABC= •AC•BE= ，∴BE= ．在Rt△ABE中，AE= =6，∴coaA= = ．

（2）解：如图2中，作PH⊥AC于H．∵PA=5t，PH=3t，AH=4t，HQ=AC﹣AH﹣CQ=9﹣9t，∴PQ2=PH2+HQ2=9t2+（9﹣9t）2．

∵S△PQM= S△QCN，∴ •PQ2= × •CQ2，∴9t2+（9﹣9t）2= ×（5t）2，整理得：5t2﹣18t+9=0，解得t=3（舍弃）或 ，∴当t= 时，满足S△PQM= S△QCN．

（3）解：①如图3中，当点M落在QN上时，作PH⊥AC于H．易知：PM∥AC，∴∠MPQ=∠PQH=60°，∴PH= HQ，∴3t= （9﹣9t），∴t= ．②如图4中，当点M在CQ上时，作PH⊥AC于H．

同法可得PH= QH，∴3t= （9t﹣9），∴t= ．综上所述：当t= s或 s时，△PQM的某个顶点（Q点除外）落在△QCN的边上．

24．（1）解：∵抛物线对称轴为直线x=1

∴﹣

∴b=2

由一元二次方程根与系数关系：

x1+x2=﹣ ，x1x2=

∴

∴

则c=﹣3

∴抛物线解析式为：y=x2﹣2x﹣3

（2）解：由（1）点D坐标为（1，﹣4）当y=0时，x2﹣2x﹣3=0解得x1=﹣1，x2=3∴点B坐标为（3，0）①设点F坐标为（a，b）∴△BDF的面积S= ×（4﹣b）（a﹣1）+ （﹣b）（3﹣a）﹣ ×2×4整理的S=2a﹣b﹣6∵b=a2﹣2a﹣3∴S=2a﹣（a2﹣2a﹣3）﹣6=﹣a2+4a﹣3∵a=﹣1＜0

∴当a=2时，S最大=﹣4+8﹣3=1②存在

由已知点D坐标为（1，﹣4），点B坐标为（3，0）∴直线BD解析式为：y=2x﹣6则点E坐标为（0，﹣6）连BC、CD，则由勾股定理

CB2=（3﹣0）2+（﹣3﹣0）2=18CD2=12+（﹣4+3）2=2BD2=（﹣4）2+（3﹣1）2=20

∴CB2+CD2=BD2

∴∠BCD=90°

∴tan∠BDC=3当点Q使得∠BDC=∠QCE时，连结QC并延长交x轴于点N，过点Q作QM⊥x轴于点M，∵∠OCN=∠QCE，CO=3∴在RtNOC中，NO=3OC=9由已知，MQ∥OE，OE=6，OB=3∴设BM=a，则MQ=2a，则MN=12-a，∵∠MQN=∠QCE，∴RtMNQ中，3MQ=MN，∴12-a=3（2a）∴a=则OM=3-=，MQ=则点Q坐标为（，）