河南省郑州市金水区一八初级中学2023年中考三模数学试卷(含答案)

2023年中招第三次适应性测试

数学试题卷

（时间：100分钟，满分：120分）

一、选择题（本大题共10小题，共30分）

1．－的相反数是（    ）

A. －             B.               C.                 D. －

2. 一个几何体的三视图如图所示，则该几何体为（    ）

A.圆柱              B.圆锥            C.四棱柱             D.四棱锥

        第2题图             第5题图                      第10题图

3．2023年1至4月，我国取得了13万亿人民币的进出口贸易。13万亿用科学记数法表示为（    ）

A．13×1012          B．1.3×10-13          C．1.3×1013          D．1.3×1011 

4. 下列运算正确的是（    ）

A. 2m×2n＝2mn        B. (x3)2＝x5                C. (3－x)2＝9－x2      D. 2x2－x2＝x2

5. 将一把直尺和一块含30°角的三角板ABC按如图所示的位置放置，若∠1＝48°，则∠2的度数为（    ）

A. 138°              B. 124°              C.  116°             D.  108°

6. 下列说法中，正确的是（    ）

A. 将一枚硬币抛掷20次，一定有10次正面朝上

B. 调查某校七年级(一)班学生的视力情况适合采用全面调查

C. 方差是反映一组数据波动大小的一个量，方差越大，波动越大；反之不成立

D. 可能性是2%的事件在一次试验中一定不会发生

7. 为了准备第八届中国诗歌节，某校组织了一次诗歌比赛，有2名女生和2名男生获得一等奖，现准备从这4名获奖学生中随机选出2名学生进行培训，将来代表学校参加第八届中国诗歌节比赛，则选出的结果是“一男一女”的概率是（    ）

A.                B.                C.                 D.

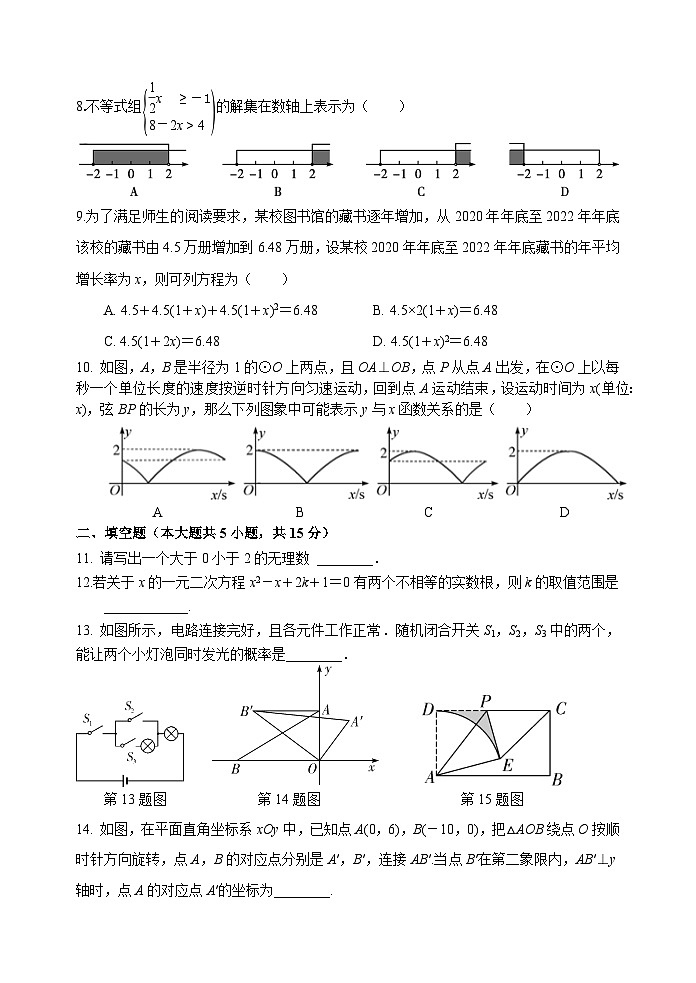
8.不等式组的解集在数轴上表示为（    ）

9.为了满足师生的阅读要求，某校图书馆的藏书逐年增加，从2020年年底至2022年年底该校的藏书由4.5万册增加到6.48万册，设某校2020年年底至2022年年底藏书的年平均增长率为x，则可列方程为（    ）

A. 4.5＋4.5(1＋x)＋4.5(1＋x)2＝6.48        B. 4.5×2(1＋x)＝6.48

C. 4.5(1＋2x)＝6.48                      D. 4.5(1＋x)2＝6.48

10. 如图，A，B是半径为1的⊙O上两点，且OA⊥OB，点P从点A出发，在⊙O上以每秒一个单位长度的速度按逆时针方向匀速运动，回到点A运动结束，设运动时间为x(单位：x)，弦BP的长为y，那么下列图象中可能表示y与x函数关系的是（    ）

       A                   B                 C                  D

二、填空题（本大题共5小题，共15分）

11. 请写出一个大于0小于2的无理数 ________．

12.若关于x的一元二次方程x2－x＋2k＋1＝0有两个不相等的实数根，则k的取值范围是____________. 

13. 如图所示，电路连接完好，且各元件工作正常．随机闭合开关S1，S2，S3中的两个，能让两个小灯泡同时发光的概率是________．

    第13题图             第14题图                    第15题图

14. 如图，在平面直角坐标系xOy中，已知点A(0，6)，B(－10，0)，把△AOB绕点O按顺时针方向旋转，点A，B的对应点分别是A′，B′，连接AB′.当点B′在第二象限内，AB′⊥y轴时，点A的对应点A′的坐标为________.        

15.如图，在矩形ABCD中，AB＝，AD＝1，点P为DC边上的一个动点，将△ADP沿AP折叠得到△AEP，DE︵为点D关于AP对称时对称点E的轨迹， 当线段EC的长度最短时，则图中阴影部分的面积是________．

三、解答题（本大题共8小题，共75分）

16.(10分)计算与化简

（1）

（2）先化简，再求值：（1）• ，其中m＝2．

17. (9分) 为参加全国防震减灾知识竞赛测试，某中学举办了校级预赛，现从八、九两个年级中各随机抽取20名学生的成绩(百分制)进行统计，将这20名学生的成绩进行了整理与分析，过程如下：

收集数据：

八年级 93 92 84 55 85 82 66 74 88 67  87 87 67 61 87 61 78 57 72 75

九年级 68 66 70 86 91 76 74 87 51 84  90 86 87 75 60 74 63 56 88 86

整理数据：

分析数据：

应用数据：

（1）填空：a＝________，b＝________，c＝________ ;

（2）你认为哪个年级学生成绩的整体水平更好，请说明理由；

（3）若该校九年级共有500名学生参加本次预赛，请你估计该校九年级学生本次成绩在80～90分(含80分但不含90分)的人数．

18. (9分) 如图，在Rt△ABC中，∠C＝90°，点O为AB边上一点，以OA为半径的☉O与BC相切于点D，分别交AB，AC边于点E，F.

（1）求证：AD平分∠BAC；

（2）若AC＝6，tan∠CAD＝，求AE的长.

19. (9分)河南省登封市境内的嵩岳寺塔是中国现存年代最久的佛塔，堪称世界上最早的筒

体建筑。某校数学社闭的同学利用所学知识来测量嵩岳寺塔的高度，如图，CD是嵩岳寺塔

附近不远处的某建筑物，他们在建筑物CD底端D处利用测角仪测得嵩岳寺塔顶端B的仰角

为60°，在建筑物CD顶端C处利用测角仪测得嵩岳寺塔底端A的俯角为35°，已知建筑物CD

的高为15米，AB⊥AD,CD⊥AD,点A,D在同一水平线上。)求嵩岳寺塔AB的高度：（结果

精确到0.1m.参考数据：sin35°≈0.57, cos35°≈0.82, tan35°≈0.70. ≈1.73

20. (9分) 如图，一次函数y＝k1x+b（k1≠0）与反比例函数y（k2≠0）的图象交于点A

（2，3），B（n，﹣1），与y轴交于点C．

（1）求反比例函数和一次函数的解析式；

（2）求△AOB的面积；

（3）直接写出不等式k1x+b≥的解集．

21. (9分) 某文具店准备购进A，B两款精美笔记本，进货价和销售价如下表：（注：利润＝销售价－进货价）

（1）文具店第一次用850元购进A、B两款笔记本共30本，求两款笔记本分别购进的本数；

（2）第一次购进的精美笔记本售完后，该文具店计划再次购进A、B两款精美笔记本共80本（进货价和销售价都不变），且进货总价不高于2200元．应如何设计进货方案，才能获得最大销售利润，最大销售利润是多少？

22. (10分) 在平面直角坐标系xOy中，已知抛物线y＝ax2＋bx-4经过点A(－4，0)，对称轴为直线x＝－1．

（1）求抛物线的解析式；

（2）当-2＜x＜3时，求y的取值范围；

（3）抛物线与y轴交于点B，直线AB上有一动点P， 将点P向下平移1.5个单位长度，得到点Q，若抛物线与线段PQ只有一个公共点，请直接写出点P的横坐标xp的取值范围．

          （备用图）

23. (10分) 在Rt△ABC中，，，点为边的中点，以为一边作正方形，

（1）如图1，点E恰好与点A重合，则线段BE与AF的数量关系为______；

（2）在（1）的条件下，

①如果正方形绕点旋转，连接、、，线段与AF的数量关系有无变化？请仅就图2的情形给出证明；

②正方形绕点旋转的过程中，当以点A，B，C，E为顶点的四边形是平行四边形时．直接写出线段AF的长．

2022-2023学年下期九年级三测数学试卷答案

一、选择题（本大题共10小题，共30分）

1．B    2. B    3．C    4. D  5. A    6. B　  7. C   8.A  9. D.   10. A

二、填空题（本大题共5小题，共15分）

11. (答案不唯一）   12.k＜－   13.     14. (，)     15.

三、解答题（本大题共8小题，共75分）

16.(10分)计算与化简

（1）

解：原式＝3-1+2  ------------------------------------3分

＝4．------------------------------------------5分

（2）先化简，再求值：（1）• ，其中m＝2．

解：原式＝（）•，

• ＝m+1，--------------------------------------------------4分

∵m＝2，

∴m+1＝2+1＝3．-------------------------------------5分

17. (9分) 解：(1)5，7，75.5；----------------------------------------------------3分

(2)八年级学生成绩的整体水平更好；

理由：∵八年级和九年级学生成绩的平均数相同，均为75.9分，九年级学生成绩的中位数和众数都小于八年级学生成绩的中位数和众数，∴八年级学生成绩的整体水平更好；----------------------------------------------------------------------------------------6分

(3)500×＝175(人)．

答：该校九年级学生本次成绩在80～90分(含80分但不含90分)的人数约有175人．------------------------------------------------------------------------------9分

18. (9分)      

（1）证明：如图，连接OD.------------------------------------------------------------1分

∵BC是☉O的切线，OD是☉O的半径，D是切点，

∴OD⊥BC.

∴∠ODB＝∠C＝90°.

∴OD∥AC.------------------------------------------------------3分

∴∠ODA＝∠CAD.

∵OD＝OA，∴∠ODA＝∠OAD.

∴∠OAD＝∠CAD.

∴AD平分∠BAC. ---------------------------------------5分

（2）解：如图，连接DE，

∵在Rt△ACD中，tan∠CAD＝, AC＝6，

∴CD=,------------------------------------------------------------------6分

∴AD=------------------------------------------7分

∵AE是直径， ∴∠ADE＝90°.

∴∠ADE＝∠C,

由（1）知∠EAD＝∠CAD.

∴△ADE∽△ACD,----------------------------------------------------------------8分

∴, 即：，

∴AE=7.5. ----------------------------------------------------------------------------9分

19. 解：(1)由题意得CD=15米，∠BDA=60°，∠CAD=35°，

在Rt△CAD中，tan∠CAD=,

∴AD=-------------------------------------3分

在Rt△ABD中，tan∠BDA=,

∴AB=AD·tan 60°， -------------------------------------------6分

∴AB=(米)，-------------------------8分

答：嵩岳寺塔AB的高度约为37.1米：----------------------9分

20. (9分)解：（1）将A（2，3）代入y得3，

解得k2＝6，∴y.-----------------------------------------------------------------1分

把B（n，﹣1）代入y得﹣1，

解得n＝﹣6，∴点B坐标为（﹣6，﹣1）．-----------------------------------2分

把A(2，3)，B（﹣6，﹣1）代入y＝k1x+b

得，---------------------------------------------------------------3分

解得，∴yx+2．---------------------------------------------------4分

（2）把x=0代入yx+2得y=2, ∴C(0,2)---------------------------------------5分

∴

=8．------------------------------------------------------------------7分

（3）x≥2或﹣6≤x＜0．------------------------------------------------------------------9分

21. 解：（1）设购进A款笔记本x本，B款笔记本y本，

依题意得：，------------------------------------------------------------------3分

解得：．------------------------------------------------------------------------------------4分

答：购进A款笔记本20本，B款笔记本10本．---------------------------------------------5分

（2）设购进m本A款笔记本，则购进本B款笔记本，

依题意得：，解得：m≤40．---------------------------------------6分

设再次购进的A、B两款精美笔记本全部售出后获得的总利润为w元，则

．-------------------------------------------7分

∵，∴w随m的增大而增大，

∴当m＝40时，w取得最大值，最大值，----------------------8分

此时．

答：当购进40本A款笔记本，40本B款笔记本时，才能获得最大销售利润，最大销售利润是1080元．--------------------------------------------------------------------------------------9分

22.解：(1)∵抛物线的对称轴为直线x＝－＝－1，①

将点A(－4，0)代入y＝ax2＋bx-4中，得②

由①，②解得a＝，b＝1.

∴抛物线的解析式为y＝x2+x－4；--------------------------3分

(2)      ∵>0,  y＝x2+x－4＝(x+1)2－,

      ∴抛物线开口向上，且当x=-1时，y最小=-. -------------5分

      ∵（-1）-（-2）＜3-（-1），

         当x=3时，y=.

      ∴当-2＜x＜3时, 当-≤y＜.--------------------------8分

(3)-4≤xp≤-3，或-1≤xp≤0.----------------------------------------10分

23. (10分) 解：（1）；-----------------------------------------2分

（2）①无变化-----------------------------------------------------3分

理由如下：在Rt△ABC中，

∵∴

∴---------------------------------5分

在正方形中，

在Rt△CEF中，

----------------------------------------6分     

∴

∵

∴  ∴

∴△ACF∽△BCE------------------------------------------------------7分

∴   ∴

∴线段与的数量关系无变化------------------------------------------8分

②或--------------------------------------10分