第02讲 菱形的判定、判定与性质综合-【暑假自学课】2023年新九年级数学暑假精品课（北师大版）

第02讲 菱形的判定、判定与性质综合

1. 掌握菱形的判定定理
2. 学会利用菱形的判定与性质综合解题

菱形的判定

菱形的判定方法有三种：

1.定义：有一组邻边相等的平行四边形是菱形.

2.对角线互相垂直的平行四边形是菱形.

3.四条边相等的四边形是菱形.

要点：前两种方法都是在平行四边形的基础上外加一个条件来判定菱形，后一种方法是在四边形的基础上加上四条边相等.

考点一：菱形的判定

例1．在下列条件中，能够判定为菱形的是（    ）

A． B． C． D．

例2．如图，添加下列条件不能判定是菱形的是（    ）.

A． B． C．平分 D．

例3．下列条件中能判断四边形是菱形的是（       ）

A．对角线互相垂直 B．对角线互相垂直且平分

C．对角线相等 D．对角线相等且互相平分

例4．如图所示，四边形，当 ，时，再下列选项中，添加一个条件，使得四边形是菱形的是（    ）

A．对角线互相平分 B．对角线相等 C．对角线互相垂直 D．有一个内角是直角

例5．在平行四边形中，添加下列条件，能判定平行四边形是菱形的是(    )

A． B． C． D．

例6．在平行四边形的对角线与相交于点O，，，，则四边形（   ）

A．平行四边形 B．矩形 C．菱形 D．正方形

例7．如图，在中，对角线、交于点O，请添加一个条件：____________，使平行四边形为菱形（不添加任何辅助线）．

例8．如图，用直尺和圆规作菱形，作图过程如下：①作锐角；②以点为圆心，以任意长度为半径作弧，与的两边分别交于点，；③分别以点，为圆心，以的长度为半径作弧，两弧相交于点，分别连接，，则四边形即为菱形，其依据是（    ）

A．一组邻边相等的四边形是菱形

B．四条边相等的四边形是菱形

C．对角线互相垂直的平行四边形是菱形

D．每条对角线平分一组对角的平行四边形是菱形

考点二：利用菱形的判定与性质求长度、角度、面积

例9．如图，在菱形中，相交于，，是线段上一点，则的度数可能是（    ）

A． B． C． D．

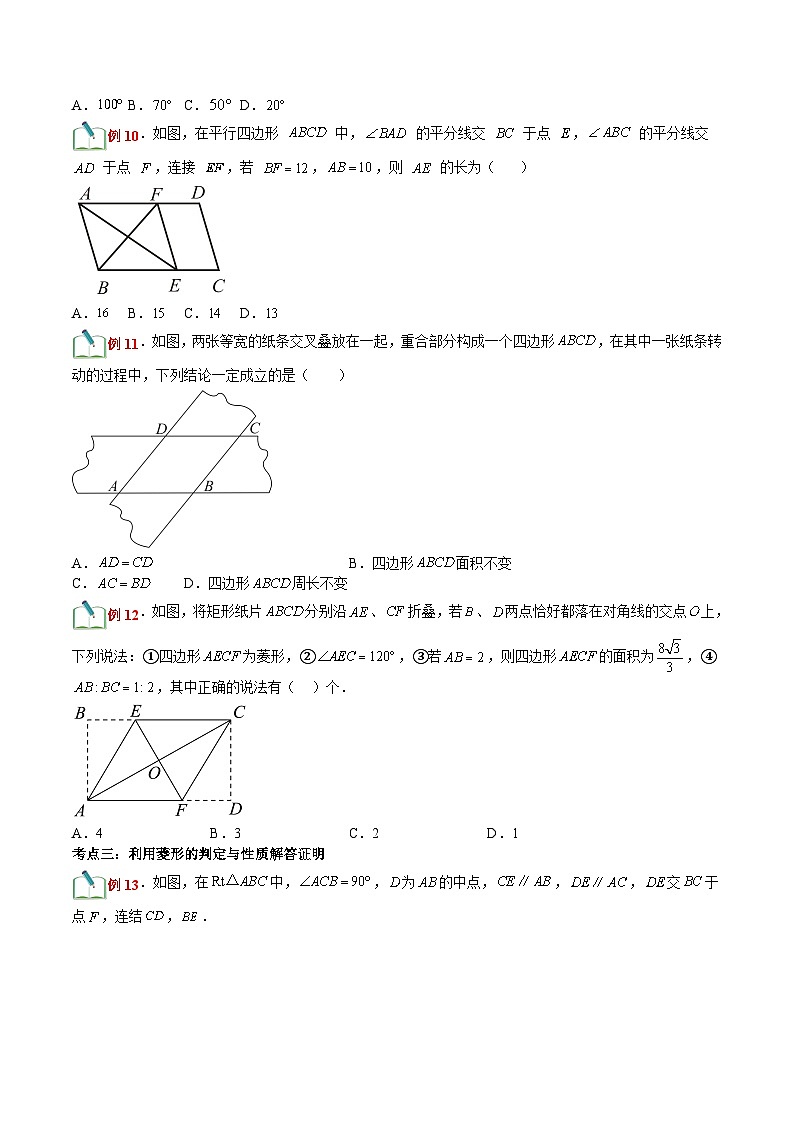
例10．如图，在平行四边形 中， 的平分线交 于点 ， 的平分线交 于点 ，连接 ，若 ，，则 的长为（      ）

A． B． C． D．

例11．如图，两张等宽的纸条交叉叠放在一起，重合部分构成一个四边形，在其中一张纸条转动的过程中，下列结论一定成立的是（　　）

A．  B．四边形面积不变

C．  D．四边形周长不变

例12．如图，将矩形纸片分别沿、折叠，若、两点恰好都落在对角线的交点上，下列说法：①四边形为菱形，②，③若，则四边形的面积为，④，其中正确的说法有（    ）个．

A．4 B．3 C．2 D．1

考点三：利用菱形的判定与性质解答证明

例13．如图，在中，，为的中点，，，交于点，连结，．

(1)求证：四边形是菱形；

(2)若，，则四边形的面积是________．

例14．如图，矩形的对角线，相交于点O，，．

(1)判断四边形的形状，并进行证明；

(2)若，，求四边形的面积．

例15．如图，在Rt△ABC中，∠BAC＝90°，D是BC的中点，，．

(1)求证：四边形ADCE是菱形；

(2)若AC＝6，AB＝8，求菱形ADCE的面积．

例16．如图，的对角线，相交于点，点作的垂线，与，分别相文于点，，连接，．

(1)求证：四边形是菱形；

(2)若，的面积是2，求的面积．

例17．如图，在平行四边形中，E为对角线上一点，过点B作，，连接，，，线段交于点H．

(1)若，求证：四边形为菱形；

(2)在（1）问的基础上，若，，求四边形的面积．

一、单选题

1．（2022·湖北襄阳·统考中考真题）如图，▱ABCD的对角线AC和BD相交于点O，下列说法正确的是（    ）

A．若OB＝OD，则▱ABCD是菱形 B．若AC＝BD，则▱ABCD是菱形

C．若OA＝OD，则▱ABCD是菱形 D．若AC⊥BD，则▱ABCD是菱形

2．（2022·甘肃兰州·统考中考真题）如图，菱形ABCD的对角线AC与BD相交于点O，E为AD的中点，连接OE，，，则（    ）

A．4 B． C．2 D．

3．（2021·内蒙古·统考中考真题）如图，在中，，和关于直线BC对称，连接AD，与BC相交于点O，过点C作，垂足为C，与AD相交于点E．若，，则的值为（   ）

A． B． C． D．

二、解答题

4．（2022·湖南郴州·统考中考真题）如图，四边形ABCD是菱形，E，F是对角线AC上的两点，且，连接BF．FD，DE，EB．

求证：四边形DEBF是菱形．

5．（2022·山东聊城·统考中考真题）如图，中，点D是AB上一点，点E是AC的中点，过点C作，交DE的延长线于点F．

(1)求证：；

(2)连接AF，CD．如果点D是AB的中点，那么当AC与BC满足什么条件时，四边形ADCF是菱形，证明你的结论．

一、单选题

1．在一组对边平行的四边形中，增加一个条件，使得这个四边形是菱形，那么增加的条件可以是（    ）

A．另一组对边相等，对角线相等 B．另一组对边相等，对角线互相垂直

C．另一组对边平行，对角线相等 D．另一组对边平行，对角线相互垂直

2．两个边长为2的等边三角形如图所示拼凑出一个平行四边形，则对角线的长为（    ）

A．2 B．4 C． D．

3．如图，在中，、分别为边、的中点，点、在上，且，若添加一个条件使四边形是菱形，则下列可以添加的条件是　　

A． B． C． D．

4．如图，在菱形ABCD中，对角线AC，BD相交于点O，点E为CD的中点．若OE＝3，则菱形ABCD的周长为（    ）

A．6 B．12 C．24 D．48

5．如图，菱形ABCD的对角线交于点O，过点A作于点E，连接OE．若，，则DE的长度为（      ）

A． B． C． D．

6．如图，在四边形中，，且，则下列说法：①四边形是平行四边形；②；③；④平分；⑤若，则四边形的面积为24．其中正确的有（     ）

A．2个 B．3个 C．4个 D．5

7．菱形中，．点、分别在边、上，且．若，则的面积为（    ）．

A． B． C． D．

8．在中，，，，点D（不与C重合）是线段上的动点，将沿翻折得，当时，四边形的面积为（    ）

A． B． C． D．

9．已知菱形 在平面直角坐标系的位置如图所示，顶点 ，点 是对角线 上的一个动点，，当 最短时，点 的坐标为（　　）

A． B． C． D．

10．如图，把菱形ABCD向右平移至DCEF的位置，作EG⊥AB，垂足为G，EG与CD相交于点K，GD的延长线交EF于点H，连接DE，则下列结论：①BG=AB+HF；②DG=DE；③∠DHE=∠BAD；④∠B=∠DEF，其中正确结论的个数是（    ）

A．1个 B．2个 C．3个 D．4个

二、填空题

11．如图，已知AD是△ABC的角平分线，DE∥AC交AB于点E，请你添加一个条件________，使四边形AEDF是菱形．

12．若▱ABCD的对角线AC平分∠DAB，则对角线AC与BD的位置关系是________．

13．四边形中，E，F，G，H分别是边，，，的中点．若四边形为菱形，则四边形应满足条件_____．

14．如图，等边的边长为，将向右平移到的位置，连接，，则的长为______．

15．如图，在四边形ABCD中，对角线AC，BD交于点O，AC与BD互相垂直且平分，BD＝6，AC＝8，则四边形周长为_____，面积为_____．

16．如图，在给定的一张平行四边形纸片上，用尺规作出四边形，具体作法如下：分别作的平分线，分别交于，连接，若，则四边形的周长是______．

17．如图，在菱形ABCD中，，∠BCD＝60°，对角线AC、BD相交于点O，点E是OC上一点，连接ED，若，则DE的长为______．

18．如图，菱形ABCD中，，AC与BD交于点O，E为CD延长线上一点，且，连结BE，分别交AC，AD于点F、G，连结OG，则下列结论：①；②；③由点A、B、D、E构成的四边形是菱形；④．其中正确的结论是______（请填写正确的序号）

三、解答题

19．已知：如图，在中，，O为垂足．求证：是菱形．

20．如图，四边形的对角线与交于点，若，，

(1)求证：四边形是平行四边形

(2)请你在不添加辅助线的情况下，添一个条件 ，使四边形是菱形

21．如图，在四边形中，与相交于点O．且，点E在上，满足．

(1)求证：；

(2)若，求证：四边形是菱形．

22．如图，平行四边形ABCD的对角线，相交于点O，且，，．

(1)求证：四边形是菱形．

(2)若，，求的长．

23．如图，线段，D是线段AC上一点，连接DE交AB于点F，若AF＝BF，求证：

(1)DF=EF；

(2)连接AE，BD，若△ABC是等边三角形∠E=30°， 求证：四边形ADBE是菱形．

24．如图，在中，交于点，点在上，．

(1)求证：四边形是平行四边形；

(2)若求证：四边形是菱形．

25．如图，在菱形中，对角线，相交于点，点，分别在，上，连接，，，．

(1)求证：；

(2)若，求菱形的周长．

26．已知在菱形ABCD中，点P在CD上，连接AP．

(1)在BC上取点Q，使得∠PAQ＝∠B，

①如图1，当AP⊥CD于点P时，求证：AP=AQ ．

②如图2，当AP与CD不垂直时，判断①中的结论（即AP=AQ）是否仍然成立，若成立，请给出证明，若不成立，则需说明理由．

(2)如图3，在CD的延长线取点N，连接AN，使得∠PAN＝∠B，若AB＝6，∠B＝60°，∠ANC＝45°，求此时线段DN的长．