




【期末分层模拟】(基础卷·浙教版)2022-2023学年八年级数学下学期期末模拟卷(原卷版+解析版)
展开编者小注:
本套专辑为浙江地区2022-2023学年第二学期期末考试研发。
7-8年级(满分100分制),分基础卷(适合80分以下学生使用)、提升卷(适合80-95分学生使用)、满分卷(适合95分以上学生使用)。
来源为近两年浙教版数学教材使用地期末原题,包含详细解析。
所有资料研发均为原创,希望助广大中学生一臂之力。
(基础卷)2022-2023学年八年级数学下学期期末考试卷(原卷版)(浙教版)
学校:___________姓名:___________班级:___________考号:___________
一、单选题(共0分
1.若反比例函数的图象经过点(2,1),则下列各点中,不在该函数图象上的是( )
A.(1,2) B.(-1,-2)
C.(-2,-1) D.(-2,1)
2.若用反证法证明命题“四边形中至少有一个角是钝角或直角”时,则首先应该假设这个四边形中( )
A.至少有一个角是钝角或直角 B.没有一个角是锐角
C.每一个角都是钝角或直角 D.每一个角是锐角
3.双减政策落地,各地学校大力提升学生核心素养,学生的综合评价分学习、体育和艺术三部分,学习成绩、体育成绩与艺术成绩按::计入综合评价,若宸宸学习成绩为分,体育成绩为分,艺术成绩为分,则他的综合评价得分为( )
A. B. C. D.
4.为了宣传环保,某学生写了一份倡议书在微博传播,规则为:将倡议书发表在自己的微博,再邀请n个好友转发倡议书,每个好友转发倡议书,又邀请n个互不相同的好友转发倡议书,以此类推,已知经过两轮传播后,共有1641人参与了传播活动,则方程列为( )
A. B. C. D.
5.已知关于方程的两个实数根是,,则方程的两个实数根是( )
A., B.,
C., D.;
6.代数式中中,x的取值范围是( )
A. B. C. D.
7.被称为“几何之父”的古希腊数学家欧几里得,在他的几何原本中,记载了用图解法解方程的方法,类似地我们可以用折纸的方法求方程的一个正根如图,一张边长为的正方形的纸片,先折出,的中点,,再沿过点的直线折叠使落在线段上,点的对应点为点,折痕为,点在边上,连接,,则长度恰好是方程的一个正根的线段为( )
A.线段 B.线段 C.线段 D.线段
8.如图,四边形是矩形,点E在线段的延长线上,连接交于点F,,点G是的中点,若,则的长为( )
A.8 B.9 C. D.
9.如图,在平行四边形中,,则的度数是( )
A. B. C. D.
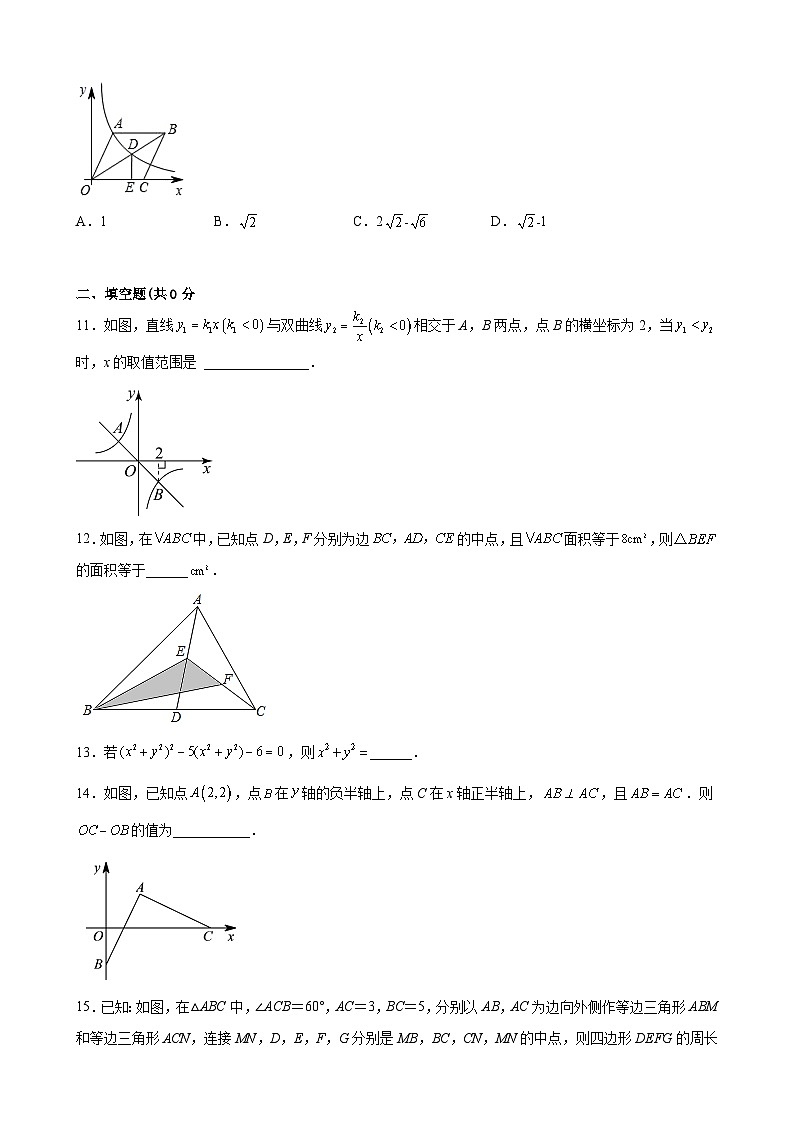
10.如图,在平面直角坐标系中,菱形ABCO的顶点O为坐标原点,边CO在x轴正半轴上,∠AOC=60°,反比例函数y=(x>0)的图象经过点A,交菱形对角线BO于点D,DE⊥x轴于点E,则CE长为( )
A.1 B. C.2﹣ D.﹣1
二、填空题(共0分
11.如图,直线与双曲线相交于A,B两点,点B的横坐标为2,当时,x的取值范围是 _______________.
12.如图,在中,已知点D,E,F分别为边的中点,且面积等于,则的面积等于______.
13.若,则______.
14.如图,已知点,点在轴的负半轴上,点C在x轴正半轴上,,且.则的值为___________.
15.已知:如图,在△ABC中,∠ACB=60°,AC=3,BC=5,分别以AB,AC为边向外侧作等边三角形ABM和等边三角形ACN,连接MN,D,E,F,G分别是MB,BC,CN,MN的中点,则四边形DEFG的周长为______.
16.已知平行四边形ABCD的两条对角线相交于平面直角坐标系中的原点O,点A(-1,3),则点C的坐标为____________.
17.若,且,,则的值是______.
18.已知,化简二次根式的正确结果为___________.
三、解答题(共0分
19.计算:
(1)×÷;
(2)(﹣)×;
(3).
20.如图1,将一长方体放置于一水平玻璃桌面上,按不同的方式摆放,记录桌面所受压强与受力面积的关系如下表所示:
桌面所受压强P(Pa) | 400 | 500 | 800 | 1000 | 1250 |
受力面积S() | 0.5 | 0.4 | a | 0.2 | 0.16 |
(1)根据表中数据,求出压强P(Pa)关于受力面积S()的函数表达式及a的值.
(2)如图2,将另一长,宽,高分别为60cm,20cm,10cm,且与原长方体相同重量的长方体放置于该水平玻璃桌面上.若玻璃桌面能承受的最大压强为2000Pa,问:这种摆放方式是否安全?请判断并说明理由.
21.为进一步提升校园阅读氛围,在第25个“世界读书日”之际,学校开展了“读书四月(单位:小时)的样本数据,结果统计如下:
四月课外阅读时间(小时) | 9 | 10 | 11 | 12 | 13 |
人数 | 7 | 11 | 10 | 9 | 8 |
(1)求出上述样本数据的众数、中位数及平均数;
(2)若该校学生人数为540人,请估计四月课外阅读时间达到12小时及以上的学生人数约为多少人.
22.已知关于x的一元二次方程.
(1)求证:方程有两个不相等的实数根;
(2)如果方程的两实根为、,且,求m的值.
23.如图,直线与双曲线交于A、B两点,与x轴交于点C,点A的纵坐标6,点B的坐标为(-3,-2).
(1)求直线和双曲线的解析式;
(2)结合图像直接写出时的取值范围.
24.如图①正方形中,点E是对角线上任意一点,连接.
(1)求证:;
(2)当时,求的度数;
(3)如图②,过点E作交于点F,当时,若.求的长.
25.如图所示,已知四边形是平行四边形,,若分别是的平分线.求的长.
26.某水果店销售一批草莓,草莓的进价为10元/千克,市场调研发现:当草莓的售价为15元/千克时,平均每天能售出8千克,而当草莓的售价每降0.5元/千克时,平均每天能多售出4千克.
(1)当草莓的售价定为12元/千克时,求该水果店每天草莓的销售量和销售利润.
(2)该水果店想在每天成本不超过200元的情况下,使得每天草莓的销售利润达到64元,售价应定为多少?
【期末分层模拟】(基础卷·苏科版)2022-2023学年八年级数学下学期期末模拟卷(原卷版+解析版): 这是一份【期末分层模拟】(基础卷·苏科版)2022-2023学年八年级数学下学期期末模拟卷(原卷版+解析版),文件包含基础卷期末考试卷解析版苏科版docx、基础卷期末考试卷原卷版苏科版docx等2份试卷配套教学资源,其中试卷共25页, 欢迎下载使用。
【期末分层模拟】(提升卷·浙教版)2022-2023学年八年级数学下学期期末模拟卷(原卷版+解析版): 这是一份【期末分层模拟】(提升卷·浙教版)2022-2023学年八年级数学下学期期末模拟卷(原卷版+解析版),文件包含提升卷期末考试卷解析版浙教版docx、提升卷期末考试卷原卷版浙教版docx等2份试卷配套教学资源,其中试卷共35页, 欢迎下载使用。
【期末分层模拟】(提升卷·浙教版)2022-2023学年七年级数学下学期期末模拟卷(原卷版+解析版): 这是一份【期末分层模拟】(提升卷·浙教版)2022-2023学年七年级数学下学期期末模拟卷(原卷版+解析版),文件包含提升卷期末考试卷解析版浙教版docx、提升卷期末考试卷原卷版浙教版docx等2份试卷配套教学资源,其中试卷共27页, 欢迎下载使用。












