【期末满分攻略】2022-2023学年人教版八年级数学下册讲学案-专题11 勾股定理之风吹荷花模型综合应用（2大类型）（原卷版+解析版）

这是一份【期末满分攻略】2022-2023学年人教版八年级数学下册讲学案-专题11 勾股定理之风吹荷花模型综合应用（2大类型）（原卷版+解析版），文件包含专题11勾股定理之风吹荷花模型综合应用2大类型解析版docx、专题11勾股定理之风吹荷花模型综合应用2大类型原卷版docx等2份学案配套教学资源，其中学案共21页， 欢迎下载使用。
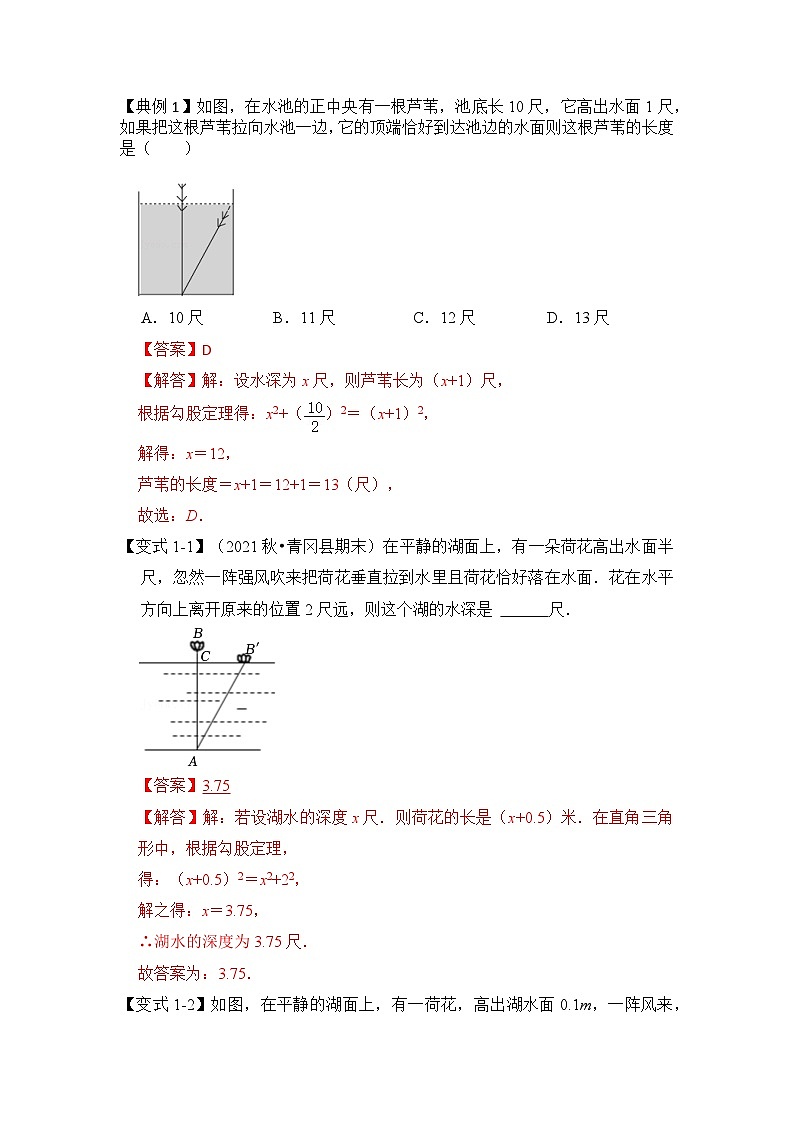
专题11  勾股定理之风吹荷花模型综合应用（2大类型）  “印度荷花问题”湖静浪平六月天，荷花半尺出水面;忽来一阵狂风急，吹倒花儿水中偃。湖面之上不复见，入秋渔翁始发现;残花离根二尺遥，试问水深尽若干?——印度数学家拜斯迦罗（公元 1114—1185 年）【模型】读诗求解“出水3尺一红莲，风吹花朵齐水面，水面移动有6尺，求水深几何请你算”。【思路】利用勾股定理建立方程，求出水深为 4.5 尺.【解析】设水深AP＝x尺， PB＝PC＝（x＋3）尺，根据勾股定理得：PA²＋AC²＝PC²，x²＋4²＝（x＋3）².解得 x=4.5.答∶水深 4.5 尺. 【典例分析】【典例1】如图，在水池的正中央有一根芦苇，池底长10尺，它高出水面1尺，如果把这根芦苇拉向水池一边，它的顶端恰好到达池边的水面则这根芦苇的长度是（　　）A．10尺 B．11尺 C．12尺 D．13尺【变式1-1】（2021秋•青冈县期末）在平静的湖面上，有一朵荷花高出水面半尺，忽然一阵强风吹来把荷花垂直拉到水里且荷花恰好落在水面．花在水平方向上离开原来的位置2尺远，则这个湖的水深是 　  　尺．【变式1-2】如图，在平静的湖面上，有一荷花，高出湖水面0.1m，一阵风来，荷花被吹到一边，花朵齐及水面．已知荷花移动的水平距离为0.3m，则这里的水深是 　 　m．【典例2】（2019春•南昌期中）如图是盼盼家新装修的房子，其中三个房间甲、乙、丙，他将一个梯子斜靠在墙上，梯子顶端距离地面的垂直距离记作MA，如果梯子的底端P不动，顶端靠在对面墙上，此时梯子的顶端距离地面的垂直距离记作NB．（1）当盼盼在甲房间时，梯子靠在对面墙上，顶端刚好落在对面墙角B处，若MA＝1.6米，AP＝1.2米，则甲房间的宽度AB＝　  　米．（2）当他在乙房间时，测得MA＝2.4米，MP＝2.5米，且∠MPN＝90°，求乙房间的宽AB；（3）当他在丙房间时，测得MA＝2.8米，且∠MPA＝75°，∠NPB＝45°．①求∠MPN的度数；②求丙房间的宽AB．  【变式2-1】（2020春•镇原县期末）如图，梯子AB靠在墙上，梯子的底端A到墙根O的距离为3m，梯子的底端A向外移动到A′，使梯子的底端A′到墙根O的距离等于4m，同时梯子的顶端B下降至B′，求BB′的长（梯子AB的长为5m）．       【变式2-2】（2022春•宁乡市期末）如图，有一架秋千，当它静止时，踏板离地的垂直高度DE＝1m，将它往前推送4m（水平距离BC＝4m）时，秋千的踏板离地的垂直高度BF＝3m，若秋千的绳索始终拉得很直，求绳索AD的长度．              【夯实基础】1．（2022春•昭化区期末）如图，将一根长为16cm的橡皮筋固定在笔直的木棒上，两端点分别记为A，B，然后将中点C向上竖直拉升6cm至点D处，则拉伸后橡皮筋的长为（　　）A．20cm B．22cm C．28cm D．32cm2．（2022秋•海淀区校级期末）如图，一支铅笔放在圆柱体笔筒中，笔筒的内部底面直径是9cm，内壁高12cm．若这支铅笔长为18cm，则这只铅笔在笔筒外面部分长度不可能的是（　　）A．2cm B．3cm C．4cm D．6cm3．有一个边长为10尺的正方形池塘，一棵芦苇生长在它的正中央，高出水面的部分为1尺，如果把该芦苇的顶端沿水池边垂直的方向拉到岸边，发现芦苇顶端恰与水面齐平，则芦苇的长度是 　 　尺．4．古诗赞美荷花：“竹色溪下绿，荷花镜里香”．平静的湖面上，一朵荷花亭亭玉立，露出水面10cm，忽见它随风斜倚，花朵恰好浸入水面，仔细观察，发现荷花偏离原地40cm（如图）．请问荷花入水部分BC长多少厘米？ 5．（2022秋•晋源区校级月考）如图，笔直的公路上A、B两点相距17km，C，D为两村庄，DA⊥AB于点A，CB⊥AB于点B，已知DA＝12km．CB＝5km，现在要在公路的AB段上建一个公交车站E，使得C，D两村到公交车站E的距离相等．则公交车站E应建在离A点多远处？   6．（2022秋•蒲江县校级期中）一架梯子AB长2.5m，如图斜靠在一面墙上，梯子底端B离墙0.7m．（1）这个梯子的顶端距地面有多高？（2）如果梯子的顶端下滑了0.4m．那么梯子底部在水平方向滑动了0.4m吗？为什么？        7．（2022春•潼南区期末）如图，一架梯子AB斜靠在某个过道竖直的左墙上，顶端在点A处，底端在水平地面的点B处．保持梯子底端B的位置不变，将梯子斜靠在竖真的右墙上，此时梯子的顶端在点C处．测得顶端A距离地面的高度AO为2米，OB为1.5米．（1）求梯子的长；（2）若顶端C距离地面的高度CD比AO多0.4米，求OD的长．   8．（2022春•藁城区校级期中）如图，在笔直的公路AB旁有一条河流，为方便运输货物，现要从公路AB上的D处建座桥梁到达C处，已知点C与公路上的停靠站A的直线距离为3km，与公路上另一停站B的直线距离为4km，且AC⊥BC，CD⊥AB．（1）求修建的桥梁CD的长；（2）桥梁CD建成后，求一辆货车由C处途经D处到达B处的总路程．      9．（2022•南京模拟）如图，有人在岸上点C的地方，用绳子拉船靠岸，开始时，绳长CB＝25米，CA⊥AB且CA＝15米，拉动绳子将船从点B沿BA方向行驶到点D后，绳长米．（1）试判定△ACD的形状，并说明理由；（2）求船体移动距离BD的长度；（3）若在BD段拉动船的速度为1米/秒，到达D后增加了人力，拉动船的速度变为2米/秒，求把船从B拉到岸边A点所用时间．【能力提升】10．（2022春•慈溪市期末）如图，一条笔直的竹竿斜靠在一道垂直于地面的增面上，一端在墙面A处，另一端在地面B处，墙角记为点C．（1）若AB＝6.5米，BC＝2.5米．①竹竿的顶端A沿墙下滑1米，那么点B将向外移动多少米？②竹竿的顶端从A处沿墙AC下滑的距离与点B向外移动的距离，有可能相等吗？如果不可能，请说明理由；如果可能，请求出移动的距离（保留根号）．（2）若AC＝BC，则顶端A下滑的距离与底端B外移的距离，有可能相等吗？若能相等，请说明理由；若不等，请比较顶端A下滑的距离与底端B外移的距离的大小．