【期末满分攻略】2022-2023学年浙教版八年级数学下册讲学案-专题10 正方形中常考四大模型

这是一份【期末满分攻略】2022-2023学年浙教版八年级数学下册讲学案-专题10 正方形中常考四大模型，文件包含期末满分攻略2022-2023学年浙教版八年级数学下册讲学案-专题10正方形中常考四大模型解析版docx、期末满分攻略2022-2023学年浙教版八年级数学下册讲学案-专题10正方形中常考四大模型原卷版docx等2份学案配套教学资源，其中学案共75页， 欢迎下载使用。

模型归纳
专题10 正方形中常考四大模型




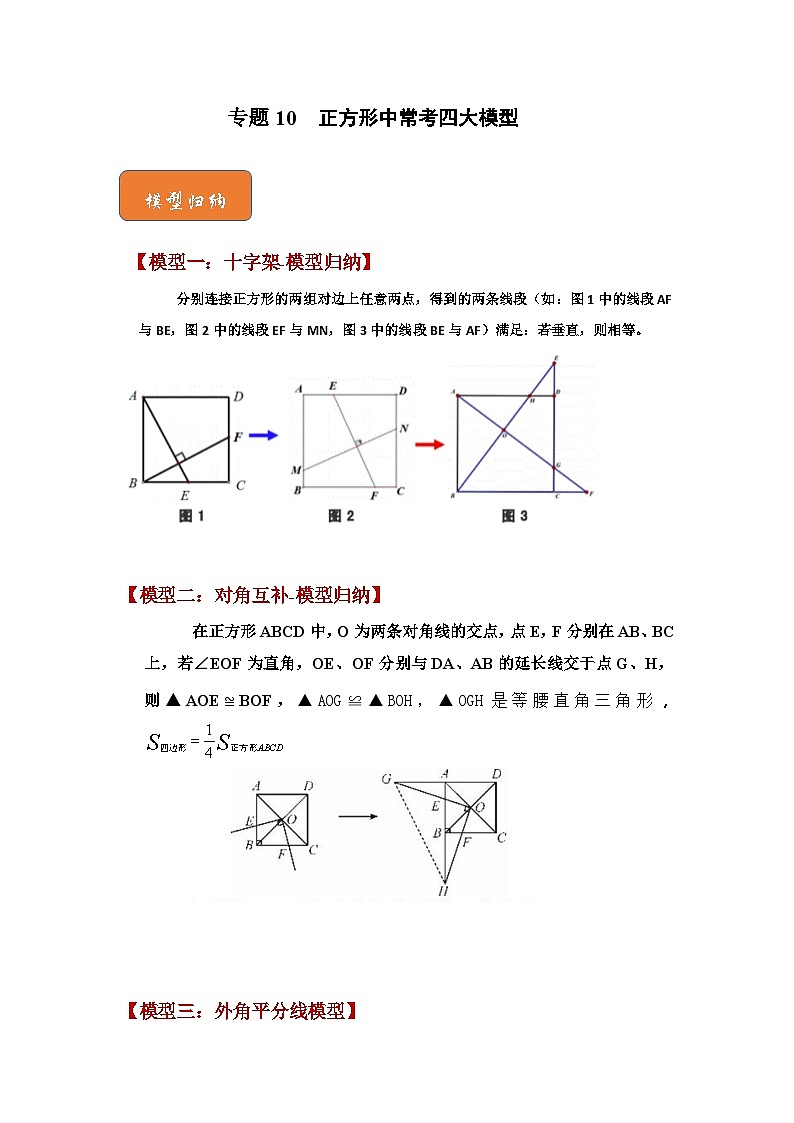
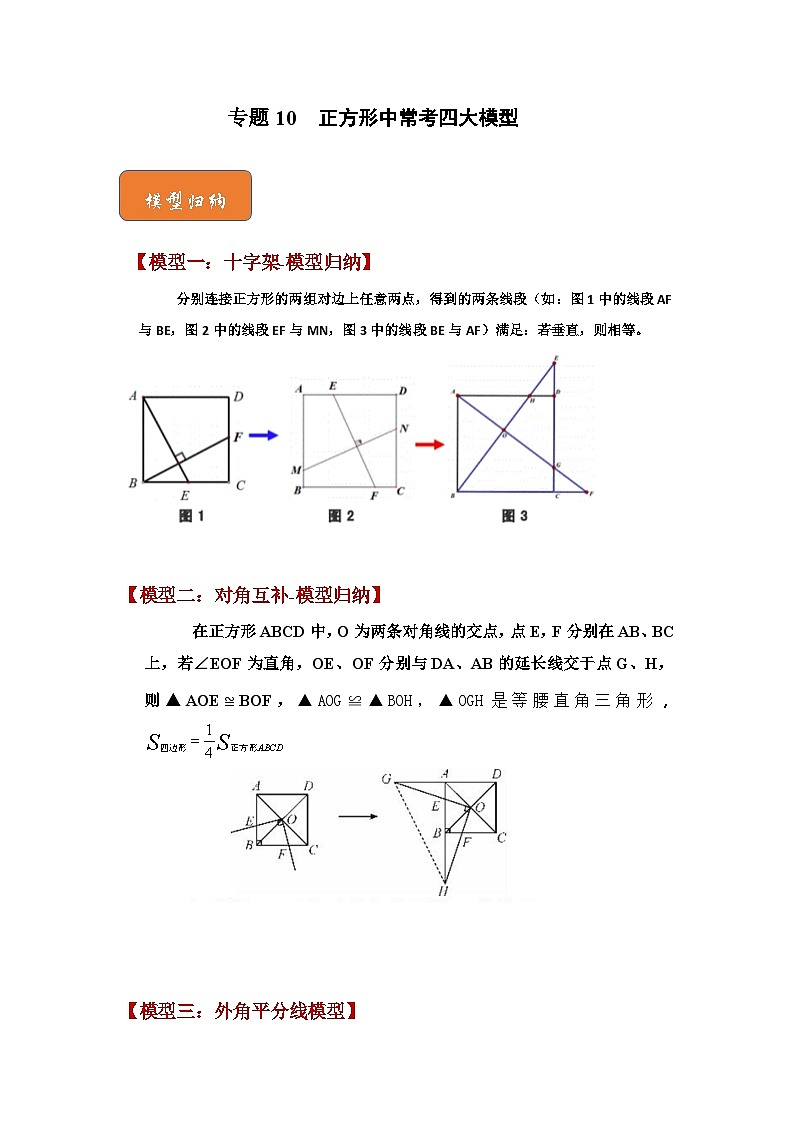
【模型一：十字架-模型归纳】
分别连接正方形的两组对边上任意两点，得到的两条线段（如：图1中的线段AF与BE，图2中的线段EF与MN，图3中的线段BE与AF）满足：若垂直，则相等。


【模型二：对角互补-模型归纳】
在正方形ABCD中，O为两条对角线的交点，点E，F分别在AB、BC上，若∠EOF为直角，OE、OF分别与DA、AB的延长线交于点G、H，则▲AOE≌BOF，▲AOG≌▲BOH，▲OGH是等腰直角三角形，



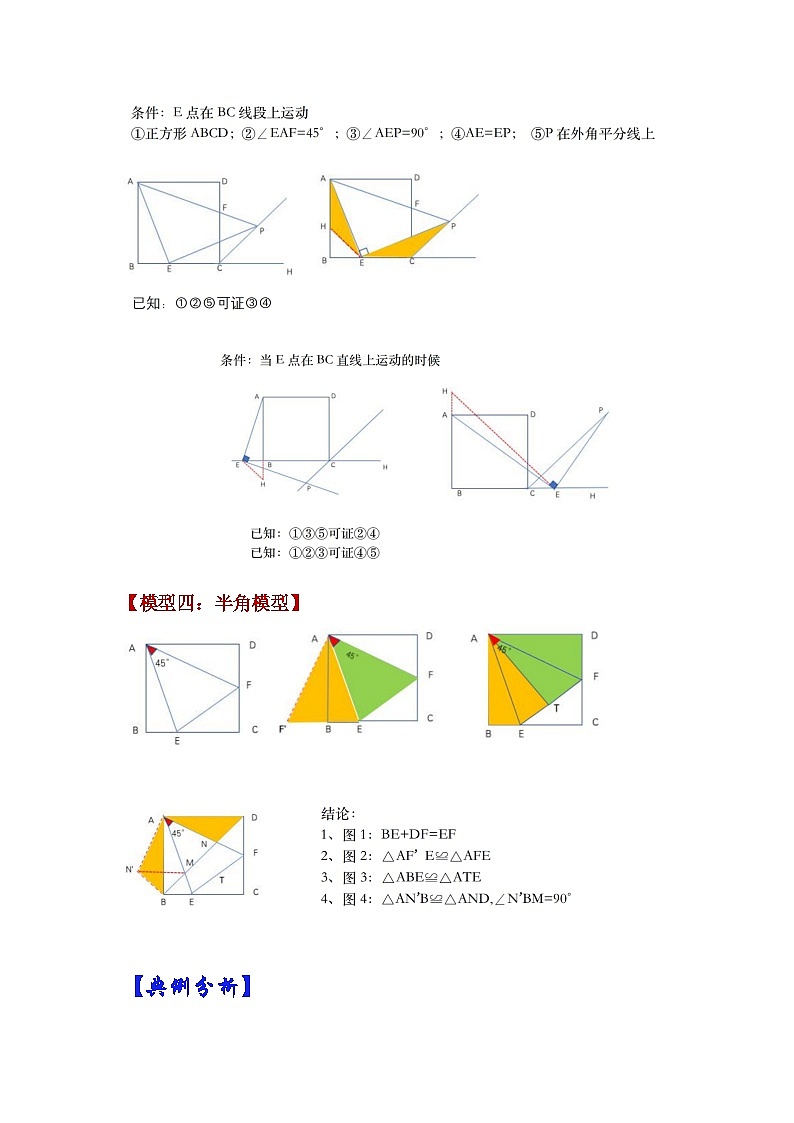
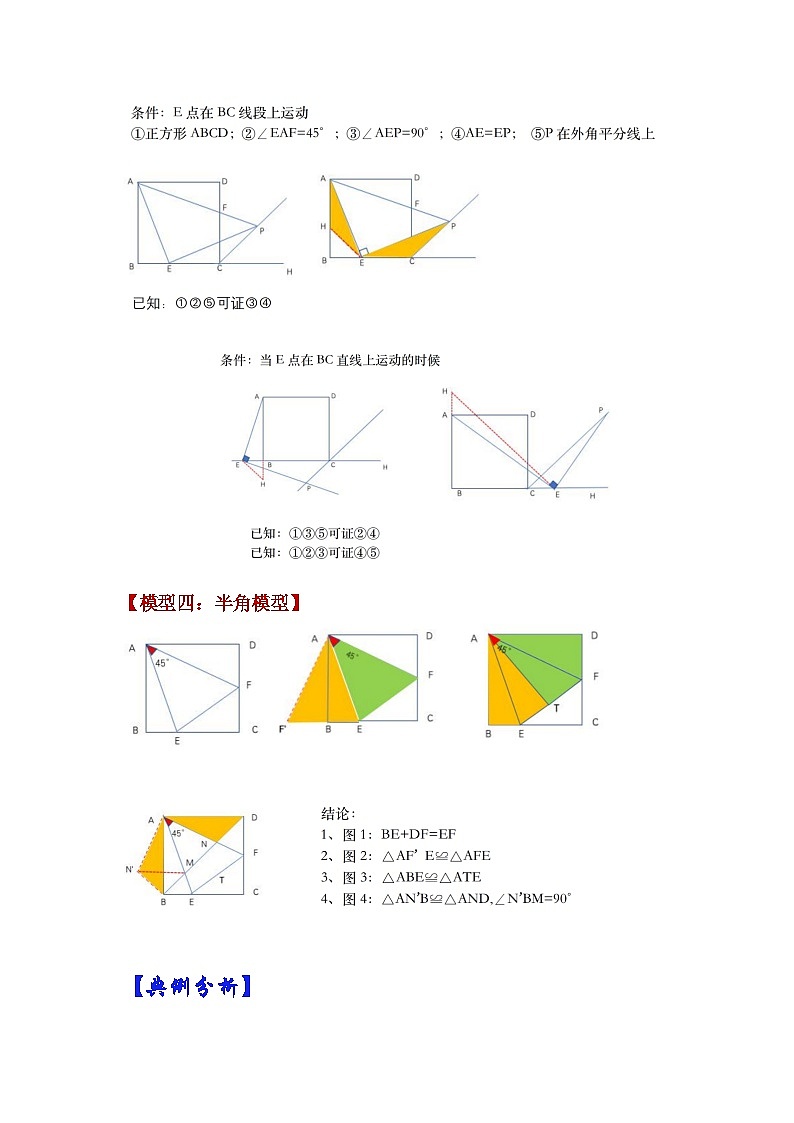
【模型三：外角平分线模型】


【模型四：半角模型】


【典例分析】
【模型1 ：“十字架”模型】
【典例1】（2022秋•三元区期中）如图，在正方形ABCD中，E、F分别是BC、CD的中点，BE＝CF，连接AF，DE交于点G，求证：
（1）△ADF≌△DCE；
（2）AF⊥DE．

【解答】证明：（1）∵四边形ABCD是正方形，
∴AD＝CD＝BC，∠ADC＝∠DCB＝90°，
∵BE＝CF，
∴BC﹣BE＝CD﹣CF，即CE＝DF，
在△ADF和△DCE中，
，
∴△ADF≌△DCE（SAS）；
（2）由（1）知△ADF≌△DCE，
∴∠DAF＝∠CDE，
∵∠ADC＝90°，即∠CDE+∠EDA＝90°，
∴∠DAF+∠EDA＝90°，
∴∠AGD＝180°﹣（∠DAF+∠EDA）＝90°，
∴AF⊥DE．
【变式1-1】（2022秋•盐津县期中）如图，在正方形ABCD中，点E，F分别在边AB，BC上，AF＝DE，AF和DE相交于点G．
（1）观察图形，写出图中所有与∠AED相等的角；
（2）线段AF与DE有怎样的位置关系，请判断并说明理由．

【解答】解：（1）由图示得出与∠AED相等的角有∠AFB，∠DAF或∠EDC．
（2）AF⊥DE．理由如下：
由正方形ABCD的性质可得，AB＝AD，∠DAB＝∠B＝90°，
在Rt△AED和Rt△BFA中，
，
∴Rt△AED≌Rt△BFA（HL），
∴∠AED＝∠AFB．
∵∠AFB+∠FAB＝90°，
∴∠AED+∠FAB＝90°，
∴∠AGE＝90°，
即AF⊥DE
【变式1-2】（2022春•广阳区校级期末）如图，在正方形ABCD中，点P在AD上，且不与A，D重合，点H在AB上，且不与A，B重合，连接BP、CH，BP与CH交于点E．
（1）若BP＝CH，求证：BP⊥CH；
（2）在（1）的条件下，若正方形ABCD的边长为12，AP＝5，求线段BE的长．

【解答】（1）证明：∵四边形ABCD是正方形，
∴AB＝BC，∠A＝∠ABC＝90°，
在Rt△PAB和Rt△HBC中，
，
∴Rt△PAB≌Rt△HBC（HL），
∴∠APB＝∠BHC，
∵∠APB+∠PBA＝90°，
∴∠CHB+∠PBA＝90°＝∠CEB，
∴BP⊥CH；
（2）解：∵正方形ABCD的边长为12，
∴AB＝BC＝12，
∵AP＝5，
由（1）Rt△PAB≌Rt△HBC得BH＝AP＝5，
在Rt△HBC中，由勾股定理得：CH＝，
∵△HBC的面积＝CH•BE＝HB•BC，
∴，
解得：BE＝，
即线段BE的长为．
【变式1-3】（2022春•海淀区校级期中）在正方形ABCD中，P是边BC上一动点（不与点B、C重合），E是AP的中点，
过点E作MN⊥AP，分别交AB、CD于点M，N．
（1）判定线段MN与AP的数量关系，并证明；
（2）连接BD交MN于点F．
①根据题意补全图形；
②用等式表示线段ME，EF，FN之间的数量关系，直接写出结论 　 　．

【解答】解：（1）MN＝AP．
证明：过点M作MG⊥CD于点G，则四边形AMGD是矩形，

∴MG＝AD，∠MGN＝90°，
∵四边形ABCD是正方形，
∴∠ABP＝90°，AB＝BC＝AD，
∴MG＝AB，∠ABP＝∠MGN，
又∵MN⊥AP，
∴∠AEM＝90°，
∴∠AME+∠BAP＝90°，
又∵∠NMG+∠AME＝90°，
∴∠NMG＝∠BAP，
∴△ABP≌△MGN（ASA），
∴AP＝MN；
（2）①补全图形如图2，

②如图3，过点P作PH∥AB交MN于点H，交BD于点K，过点M作MG⊥CD于点G，

∵AM∥PH，
∴∠MAE＝∠EPH，
∵E为AP的中点，
∴AE＝EP，
又∵∠AEM＝∠PEH，
∴△AME≌△PHE（ASA），
∴ME＝EH，AM＝PH，
∵四边形AMGD是矩形，
∴AM＝DG，
∴DG＝PH，
∵∠CBD＝45°，∠BPK＝90°，
∴∠BPK＝∠BKP＝45°，
∴BP＝PK，
由（1）知△ABP≌△MGN，
∴BP＝NG，
∴PK＝NG，
∴HK＝DN，
又∵NK∥DN，
∴∠HKF＝∠NDF，
∴△HKF≌△NDF（AAS），
∴HF＝NF，
∴EF＝EH+HF＝EM+FN．
故答案为：EF＝EM+FN．
【模型2 ：“对角互补”模型】
【典例2】（2021春•宁阳县期末）如图，已知四边形ABCD是正方形，对角线AC、BD相交于O．
（1）如图1，设E、F分别是AD、AB上的点，且∠EOF＝90°，线段AF、BF和EF之间存在一定的数量关系．请你用等式直接写出这个数量关系；
（2）如图2，设E、F分别是AB上不同的两个点，且∠EOF＝45°，请你用等式表示线段AE、BF和EF之间的数量关系，并证明．

【答案】（1） EF2＝AF2+BF2 （2）EF2＝BF2+AE2
【解答】解：（1）EF2＝AF2+BF2．
理由：如图1，∵四边形ABCD是正方形，
∴OA＝OB，∠OAE＝∠OBF＝45°，AC⊥BD，
∴∠EOF＝∠AOB＝90°，
∴∠EOA＝∠FOB，
在△EOA和△FOB中，
，
∴△EOA≌△FOB（ASA），
∴AE＝BF，
在Rt△EAF中，EF2＝AE2+AF2＝AF2+BF2；
（2）在BC上取一点H，使得BH＝AE．

∵四边形ABCD是正方形，
∴OA＝OB，∠OAE＝∠OBH，∠AOB＝90°，
在△OAE和△OBH中，

∴△OAE≌△OBH（SAS），
∴AE＝BH，∠AOE＝∠BOH，OE＝OH，
∵∠EOF＝45°，
∴∠AOE+∠BOF＝45°，
∴∠BOF+∠BOH＝45°，
∴∠FOE＝∠FOH＝45°，
在△FOE和△FOH中•，
，
∴△FOE≌△FOH（SAS），
∴EF＝FH，
∵∠FBH＝90°，
∴FH2＝BF2+BH2，
∴EF2＝BF2+AE2，
【变式2-1】（2020•呼伦贝尔）已知：如图，在正方形ABCD中，对角线AC，BD相交于点O，点E，F分别是边BC，CD上的点，且∠EOF＝90°．
求证：CE＝DF．

【答案】略
【解答】证明：∵四边形ABCD为正方形，
∴OD＝OC，∠ODF＝∠OCE＝45°，∠COD＝90°，
∴∠DOF+∠COF＝90°，
∵∠EOF＝90°，即∠COE+∠COF＝90°，
∴∠COE＝∠DOF，
∴△COE≌△DOF（ASA），
∴CE＝DF．
【典例3】（2020春•潜山市期末）如图，已知四边形ABCD为正方形，AB＝3，点E为对角线AC上一动点，连接DE，过点E作EF⊥DE，交BC于点F，以DE、EF为邻边作矩形DEFG，连接CG．
（1）求证：矩形DEFG是正方形；
（2）探究：CE+CG的值是否为定值？若是，请求出这个定值；若不是，请说明理由．

【答案】（1）略 （2）CE+CG＝CE+AE＝AC＝AB＝×3＝6是定值．
【解答】解：（1）如图，作EM⊥BC于M，EN⊥CD于N，
∴∠MEN＝90°，
∵点E是正方形ABCD对角线上的点，
∴EM＝EN，
∵∠DEF＝90°，
∴∠DEN＝∠MEF，
∵∠DNE＝∠FME＝90°，
在△DEN和△FEM中，
，
∴△DEN≌△FEM（ASA），
∴EF＝DE，
∵四边形DEFG是矩形，
∴矩形DEFG是正方形；

（2）CE+CG的值是定值，定值为6，理由如下：
∵正方形DEFG和正方形ABCD，
∴DE＝DG，AD＝DC，
∵∠CDG+∠CDE＝∠ADE+∠CDE＝90°，
∴∠CDG＝∠ADE，
在∴△ADE和△CDG中，，
∴△ADE≌△CDG（SAS），
∴AE＝CG，
∴CE+CG＝CE+AE＝AC＝AB＝×3＝6是定值．


【变式3-1】（2021春•淮北期末）四边形ABCD为正方形，点E为线段AC上一点，连接DE，过点E作EF⊥DE，交射线BC于点F，以DE、EF为邻边作矩形DEFG，连接CG．
（1）如图，求证：矩形DEFG是正方形；
（2）若AB＝2，CE＝2，求CG的长；
（3）当线段DE与正方形ABCD的某条边的夹角是40°时，直接写出∠EFC的度数．

【答案】（1）略 （2）CG＝2 （3）∠EFC＝130°或40°
【解答】（1）证明：作EP⊥CD于P，EQ⊥BC于Q，
∵∠DCA＝∠BCA，
∴EQ＝EP，
∵∠QEF+∠FEC＝45°，∠PED+∠FEC＝45°，
∴∠QEF＝∠PED，
在Rt△EQF和Rt△EPD中，，
∴Rt△EQF≌Rt△EPD（ASA），
∴EF＝ED，
∴矩形DEFG是正方形；

（2）如图2中，在Rt△ABC中，AC＝AB＝4，
∵EC＝2，
∴AE＝CE，
∴点F与C重合，此时△DCG是等腰直角三角形，易知CG＝2；

（3）①如图3，当DE与AD的夹角为40°时，
∠DEC＝45°+40°＝85°，
∵∠DEF＝90°，
∴∠CEF＝5°，
∵∠ECF＝45°，
∴∠EFC＝130°，

②如图4，当DE与DC的夹角为40°时，
∵∠DEF＝∠DCF＝90°，
∴∠EFC＝∠EDC＝40°，

综上所述，∠EFC＝130°或40°．


【变式3-2】（2021•杭州校级模拟）如图，正方形ABCD中，AB＝4，点E是对角线AC上的一点，连接DE．过点E作EF⊥ED，交AB于点F，以DE、EF为邻边作矩形DEFG，连接AG．
（1）求证：矩形DEFG是正方形；
（2）求AG+AE的值；
（3）若F恰为AB中点，连接DF交AC于点M，请直接写出ME的长．

【答案】（1）略 （2） AE+AG＝4． （3）ME=
【解答】解：（1）如图，作EM⊥AD于M，EN⊥AB于N．
∵四边形ABCD是正方形，
∴∠EAD＝∠EAB，
∵EM⊥AD于M，EN⊥AB于N，
∴EM＝EN，
∵∠EMA＝∠ENA＝∠DAB＝90°，
∴四边形ANEM是矩形，
∵EF⊥DE，
∴∠MEN＝∠DEF＝90°，
∴∠DEM＝∠FEN，
∵∠EMD＝∠ENF＝90°，
∴△EMD≌△ENF，
∴ED＝EF，
∵四边形DEFG是矩形，
∴四边形DEFG是正方形．
（2）∵四边形DEFG是正方形，四边形ABCD是正方形，
∴DG＝DE，DC＝DA＝AB＝4，∠GDE＝∠ADC＝90°，
∴∠ADG＝∠CDE，
∴△ADG≌△CDE（SAS），
∴AG＝CE，
∴AE+AG＝AE+EC＝AC＝AD＝4．
（3）如图，作EH⊥DF于H．
∵四边形ABCD是正方形，
∴AB＝AD＝4，AB∥CD，
∵F是AB中点，
∴AF＝FB
∴DF＝＝2，
∵△DEF是等腰直角三角形，EH⊥AD，
∴DH＝HF，
∴EH＝DF＝，
∵AF∥CD，
∴AF：CD＝FM：MD＝1：2，
∴FM＝，
∴HM＝HF﹣FM＝，
在Rt△EHM中，EM＝＝
【模型3 ：“外角平分线”模型】
【典例4】（春•双鸭山期末）如图，四边形ABCD是正方形，E是BC边所在直线上的点，∠AEF＝90°，且EF交正方形外角∠DCG的平分线CF于点F．
（1）当点E在线段BC中点时（如图1），易证AE＝EF，不需证明；
（2）当点E在线段BC上（如图2）或在线段BC延长线上（如图3）时，（1）中的结论是否仍然成立？请写出你的猜想，并选择图2或图3的一种结论给予证明．

【答案】 （2）成立
【解答】解：（1）取AB中点M，连接ME，
∵点E在线段BC中点，点M是AB中点，
∴AM＝BM＝BE＝CE
∴∠BME＝45°，
∴∠AME＝135°，
∵CF是外角平分线，
∴∠DCF＝45°，
∴∠ECF＝135°，
∴∠AME＝∠ECF，
∵∠AEB+∠BAE＝90°，∠AEB+∠CEF＝90°，
∴∠BAE＝∠CEF，
∴△AME≌△ECF（ASA），
∴AE＝EF．

（2）图2：结论是AE＝EF
理由如下：
在AB上取一点M，使AM＝EC，连接ME．
∴BM＝BE，
∴∠BME＝45°，
∴∠AME＝135°，
∵CF是外角平分线，
∴∠DCF＝45°，
∴∠ECF＝135°，
∴∠AME＝∠ECF，
∵∠AEB+∠BAE＝90°，∠AEB+∠CEF＝90°，
∴∠BAE＝∠CEF，
∴△AME≌△ECF（ASA），
∴AE＝EF．

图3结论是AE＝EF，
理由如下：
在BA的延长线上取一点N．
使AN＝CE，连接NE．
∴BN＝BE，
∴∠N＝∠NEC＝45°，
∵CF平分∠DCG，
∴∠FCE＝45°，
∴∠N＝∠ECF，
∵四边形ABCD是正方形，
∴AD∥BE，
∴∠DAE＝∠BEA，
即∠DAE+90°＝∠BEA+90°，
∴∠NAE＝∠CEF，
∴△ANE≌△ECF（ASA），
∴AE＝EF．



【变式4-1】（春•海淀区校级期中）如图，四边形ABCD是正方形，点E是边BC上一点，且∠AEF＝90°，且EF交正方形外角平分线CF于点F．若正方形边长是8，EC＝2，则FC的长为　 　．

【答案】6
【解答】解：在AB上取点P，使AP＝CE，连接EP，
∵四边形ABCD是正方形，
∴AB＝BC，∠B＝∠BCD＝90°，
∵AP＝EC，
∴BP＝BE，
∴∠BPE＝45°，∠APE＝135°，
∵CF是正方形外角的平分线，
∴∠ECF＝135°，
∵∠AEF＝90°，∠B＝90°，
∴∠BAE＝∠CEF，
在△PAE和△CEF中，，
∴△PAE≌△CEF（ASA），
∴PE＝CF，
∵AB＝BC＝8，AP＝CE＝2，
∴PB＝BE＝6，
∴CF＝PE＝PB＝6；
故答案为：6．


【变式4-2】（2021春•柳南区校级期末）如图1，四边形ABCD是正方形，点E是边BC的中点，∠AEF＝90°，且EF交正方形ABCD的外角∠DCG的平分线CF于点F．
（1）如图2，取AB的中点H，连接HE，求证：AE＝EF．
（2）如图3，若点E是BC的延长线上（除C点外）的任意一点，其他条件不变结论“AE＝EF”仍然成立吗？如果正确，写出证明过程：如果不正确，请说明理由．

【答案】（1）略 （2）AE＝EF成立
【解答】（1）证明：取AB的中点H，连接EH；如图1所示

∵四边形ABCD是正方形，AE⊥EF；
∴∠1+∠AEB＝90°，∠2+∠AEB＝90°
∴∠1＝∠2，
∵BH＝BE，∠BHE＝45°，且∠FCG＝45°，
∴∠AHE＝∠ECF＝135°，AH＝CE，
在△AHE和△ECF中，
，
∴△AHE≌△ECF（ASA），
∴AE＝EF；

（2）解：AE＝EF成立，
理由如下：如图2，延长BA到M，使AM＝CE，

∵∠AEF＝90°，
∴∠FEG+∠AEB＝90°．
∵∠BAE+∠AEB＝90°，
∴∠BAE＝∠FEG，
∴∠MAE＝∠CEF．
∵AB＝BC，
∴AB+AM＝BC+CE，
即BM＝BE．
∴∠M＝45°，
∴∠M＝∠FCE．
在△AME与△ECF中，
，
∴△AME≌△ECF（ASA），
∴AE＝EF．

【变式4-3】（春•西乡塘区期末）如图所示，BD是正方形ABCD的对角线，BC＝4，点H是AD边上的一动点，连接CH，作HE⊥CH，使得HE＝CH，连接AE．
（1）求证：∠DCH＝∠AHE；
（2）如图2，过点E作EF∥AD交对角线BD于点F，试探究：在点H的运动过程中，EF的长度是否为一个定值；如果是，请求出EF的长度．

【答案】（1） 略 （2）EF的长度是一个定值，且EF＝4
【解答】（1）证明：如图1，∵四边形ABCD是正方形，
∴∠CDH＝90°，
∴∠DCH+∠CHD＝90°，
∵HE⊥CH，
∴∠CHE＝∠CHD+∠AHE＝90°，
∴∠DCH＝∠AHE；
（2）解：EF的长度是一个定值，且EF＝4；

理由是：如图2，在CD取一点M，使CM＝AH，连接HM，
∵CD＝AD，
∴DM＝DH，
∵∠CDH＝90°，
∴∠DMH＝45°，
∴∠CMH＝135°，
在△CMH和△HAE中，
∵，
∴△CMH≌△HAE（SAS），
∴∠HAE＝∠CMH＝135°，
∴∠EAG＝45°＝∠ADB，
∴DF∥AE，
∵EF∥AD，
∴四边形AEFD是平行四边形，
∴EF＝AD＝BC＝4．
【模型4：“半角”模型】
【典例5】（春•十堰期末）如图，在正方形OABC中，点B的坐标是（6，6），点E、F分别在边BC、BA上，OE＝3．若∠EOF＝45°，则F点的纵坐标是（　　）

A．2 B． C． D．﹣1
【答案】A
【解答】解：如图，连接EF，延长BA，使得AM＝CE，
在△OCE和△OAM中，
，
∴△OCE≌△OAM（SAS）．

∴OE＝OM，∠COE＝∠MOA，
∵∠EOF＝45°，
∴∠COE+∠AOF＝45°，
∴∠MOA+∠AOF＝45°，
∴∠EOF＝∠MOF，
在△OFE和△OFM中，
，
∴△OFE≌△FOM（SAS），
∴EF＝FM＝AF+AM＝AF+CE，
设AF＝x，
∵CE＝＝＝3，
∴EF＝3+x，EB＝3，FB＝6﹣x，
∴（3+x）2＝32+（6﹣x）2，
∴x＝2，
∴点F的纵坐标为2，
故选：A．
【变式5-1】（溧水区二模）如图，在正方形OABC中，点B的坐标是（4，4），点E、F分别在边BC、BA上，OE＝2．若∠EOF＝45°，则F点的纵坐标是（　　）

A．1 B． C． D．﹣1
【答案】B
【解答】解：如图，连接EF，延长BA，使得AM＝CE，
∵OA＝OC，∠OCE＝∠AOM，
∴△OCE≌△OAM（SAS）．

∴OE＝OM，∠COE＝∠MOA，
∵∠EOF＝45°，
∴∠COE+∠AOF＝45°，
∴∠MOA+∠AOF＝45°，
∴∠EOF＝∠MOF，
在△OFE和△OFM中，
，
∴△OFE≌△FOM（SAS），
∴EF＝FM＝AF+AM＝AF+CE，设AF＝x，
∵CE＝＝＝2，
∴EF＝2+x，EB＝2，FB＝4﹣x，
∴（2+x）2＝22+（4﹣x）2，
∴x＝，
∴点F的纵坐标为，
故选：B
【典例6】（罗湖区校级期末）如图，正方形ABCD的边长为4，点E，F分别在AB，AD上，若CE＝2，且∠ECF＝45°，则CF的长为（　　）

A． B． C． D．
【答案】A
【解答】解：把△FCD绕点C逆时针旋转90°得△F′CB，此时E，B，F'三点共线，

则△CBF'≌△CDF，连接EF．
∴CF＝CF′，
∵∠FCF′＝90°，
∴∠ECF＝45°，
∴∠ECF＝∠ECF′＝45°，
∵CE＝CE，
∴△CEF≌△CEF'（SAS），
∴EF＝EF'．
在Rt△EBC中，，
∴AE＝AB﹣BE＝2．
设DF＝x，则AF＝4﹣x．
∵DF＝BF′，
∴EF＝EF'＝BE+BF'＝2+x，
在Rt△FCD中，EF2＝AE2+AF2，
∴（2+x）2＝22+（4﹣x）2，
解得：．
在Rt△CDF中，，
∴，
解得：．
故选：A．
【变式6-1】（防城区期中）如图，正方形ABCD的边长为4，点E，F分别在AB，AD上，若CE＝5，且∠ECF＝45°，则CF的长为　　．

【答案】
【解答】解：如图，延长FD到G，使DG＝BE；
连接CG、EF；
∵四边形ABCD为正方形，
在△BCE与△DCG中，，
∴△BCE≌△DCG（SAS），
∴CG＝CE，∠DCG＝∠BCE，
∴∠GCF＝45°，
在△GCF与△ECF中，，
∴△GCF≌△ECF（SAS），
∴GF＝EF，
∵CE＝5，CB＝4，
∴BE＝3，
∴AE＝1，
设AF＝x，则DF＝4﹣x，GF＝3+（4﹣x）＝7﹣x，
∴EF＝＝，
∴（7﹣x）2＝1+x2，
∴x＝，
即AF＝，
∴DF＝4﹣＝，
∴CF＝＝＝，
故答案为：．

【典例7】（2021春•澄城县期末）正方形ABCD的边长为6，E，F分别是AB，BC边上的点，且∠EDF＝45°，将△DAE绕点D逆时针旋转90°，得到△DCM．
（1）求证：EF＝CF+AE；
（2）当AE＝2时，求EF的长．

【答案】（1） 略 （2）EF＝5
【解答】（1）证明：∵△DAE逆时针旋转90°得到△DCM，
∴∠FCM＝∠FCD+∠DCM＝180°，AE＝CM，
∴F、C、M三点共线，
∴DE＝DM，∠EDM＝90°，
∴∠EDF+∠FDM＝90°，
∵∠EDF＝45°，
∴∠FDM＝∠EDF＝45°，
在△DEF和△DMF中，
∵，
∴△DEF≌△DMF（SAS），
∴EF＝MF，
∴EF＝CF+AE；

（2）解：设EF＝MF＝x，
∵AE＝CM＝2，且BC＝6，
∴BM＝BC+CM＝6+2＝8，
∴BF＝BM﹣MF＝BM﹣EF＝8﹣x，
∵EB＝AB﹣AE＝6﹣2＝4，
在Rt△EBF中，由勾股定理得EB2+BF2＝EF2，
即42+（8﹣x）2＝x2，
解得：x＝5，
则EF＝5．

【变式7-1】（2020•饶平县校级模拟）如图，已知正方形ABCD的边长为3，E、F分别是AB、BC边上的点，且∠EDF＝45°，将△DAE绕点D按逆时针方向旋转90°得到△DCM．
（1）求证：EF＝MF；
（2）当AE＝1时，求EF的长．

【答案】（1）略 （2）EF的长为．
【解答】（1）证明：∵△DAE绕点D逆时针旋转90°得到△DCM，
∴DE＝DM，∠EDM＝90°，F，C，M三点共线，
∵∠EDF＝45°，
∴∠FDM＝45°，
∴∠EDF＝∠FDM．
又∵DF＝DF，DE＝DM，
∴△DEF≌△DMF，
∴EF＝MF；

（2）解：设EF＝MF＝x，
∵AE＝CM＝1，AB＝BC＝3，
∴EB＝AB﹣AE＝3﹣1＝2，BM＝BC+CM＝3+1＝4，
∴BF＝BM﹣MF＝4﹣x．
在Rt△EBF中，由勾股定理得EB2+BF2＝EF2，
即22+（4﹣x）2＝x2，
解得：x＝，
则EF的长为．

【变式7-2】（春•越秀区校级期中）（1）如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF＝BE，
求证：CE＝CF．
（2）如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE＝45°，求证：GE＝BE+GD．
（3）运用（1）（2）解答中所积累的经验和知识，完成下题：
如图3，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B＝90°，AB＝BC＝12．E是AB上一点，且∠DCE＝45°，BE＝4，求直角梯形ABCD的面积．

【答案】（1） 略 （2）略 （3）108．
【解答】解：（1）证明：如图1，

∵四边形ABCD是正方形，
∴BC＝CD，∠B＝∠CDF＝90°，
又∵BE＝DF，
∴△CBE≌△CDF（SAS），
∴CE＝CF；
（2）成立．
∵∠GCE＝45°，
∴∠BCE+∠GCD＝45°，
∵△BEC≌△DFC，
∴∠BCE＝∠DCF，
∴∠DCF+∠GCD＝45°，即∠GCF＝45°，
∴∠GCE＝∠GCF，且GC＝GC，CE＝CF，
∴△GCE≌△GCF（SAS），
∴GE＝GF，
∴GE＝GD+DF＝BE+GD；
（3）如图：过点C作CF⊥AD于F，

∵AD∥BC，∠B＝90°，
∴∠A＝90°，
∵∠A＝∠B＝90°，FC⊥AD，
∴四边形ABCF是矩形，且AB＝BC＝12，
∴四边形ABCF是正方形，
∴AF＝12，
由（2）可得DE＝DF+BE，
∴DE＝4+DF，
在△ADE中，AE2+DA2＝DE2．
∴（12﹣4）2+（12﹣DF）2＝（4+DF）2．
∴DF＝6，
∴AD＝6，
∴S四边形ABCD＝＝＝108
【夯实基础】
1．（2022秋•碑林区校级期末）如图，在边长为的正方形ABCD中，∠CDE＝30°，DE⊥CF，则AF的长为（　　）

A． B． C． D．
【答案】D
【解答】解：∵四边形ABCD是正方形，
∴CD＝BC＝AB＝4，∠BCD＝∠B＝90°，
∵DE⊥CF，
∴∠CDE+∠DCF＝90°＝∠DCF+∠BCF，
∴∠CDE＝∠BCF＝30°，
∴BC＝BF＝4，
∴BF＝4，
∴AF＝AB﹣BF＝4﹣4，
故选：D．
2．（2022秋•阜平县月考）如图所示，E、F、G、H分别为正方形ABCD的边AB，BC，CD，DA上的点，且AE＝BF＝CG＝DH＝AB，则图中阴影部分的面积与正方形ABCD的面积之比为（　　）

A． B． C． D．
【答案】A
【解答】解：

∵四边形ABCD是正方形，
∴BC＝AB＝AD，∠DAB＝∠ABF＝90°，
∵AE＝AB，BF＝BC，
∴△DAE≌△ABF（SAS），
∴∠ADM＝∠BAN，
∵∠BAN+∠DAM＝90°，
∴∠ADM+DAM＝90°，
∴∠AMD＝90°，
同理：∠ANB＝90°，
∴∠AMD＝∠ANB，
∴△DAM≌△ABN（AAS），
∴AM＝BN，
同理可以证明△BCP，△CDQ，△DAM，△ABN是全等的直角三角形，它们的面积相等，
∵BE＝AB，DG＝DC，AB∥DC，
∴四边形EBGD是平行四边形，
∴ED∥BG，
∴AM：AN＝AE：AB＝1：4，
令正方形ABCD的边长是a，AM＝b，则BN＝b，AN＝4b，
∴正方形ABCD的面积是a2，△ABN的面积是b•4b＝2b2，
∵AB2＝BN2+AN2，
∴a2＝b2+16b2＝17b2，
∵阴影的面积＝a2﹣4×2b2＝17b2﹣8b2＝9b2，
∴阴影部分的面积与正方形ABCD的面积的比是＝．
故选：A．
3．（2022秋•汝州市期末）如图，在正方形ABCD中，E、F分别是AB，BC的中点，CE，DF交于点G，连接AG，下列结论：①CE＝DF；②CE⊥DF；③∠AGE＝∠CDF；④∠EAG＝30°，其中正确的结论是（　　）

A．①② B．①③ C．①②④ D．①②③
【答案】D
【解答】解：∵四边形ABCD是正方形，
∴AB＝BC＝CD＝AD，∠B＝∠BCD＝90°，
∵E，F分别是AB，BC的中点，
∴BE＝AB，CF＝BC，
∴BE＝CF，
在△CBE与△DCF中，
，
∴△CBE≌△DCF（SAS），
∴∠ECB＝∠CDF，CE＝DF，故①正确；
∵∠BCE+∠ECD＝90°，
∴∠ECD+∠CDF＝90°，
∴∠CGD＝90°，
∴CE⊥DF，故②正确；
∴∠EGD＝90°，
延长CE交DA的延长线于H，

∵点E是AB的中点，
∴AE＝BE，
∵∠AHE＝∠BCE，∠AEH＝∠CEB，AE＝BE，
∴△AEH≌△BEC（AAS），
∴BC＝AH＝AD，
∵AG是斜边的中线，
∴AG＝DH＝AD，
∴∠ADG＝∠AGD，
∵∠AGE+∠AGD＝90°，∠CDF+∠ADG＝90°，
∴∠AGE＝∠CDF．故③正确；
∵CF＝BC＝CD，
∴∠CDF≠30°，
∴∠ADG≠60°，
∵AD＝AG，
∴△ADG不是等边三角形，
∴∠EAG≠30°，故④错误；
故选：D．
4．（2022秋•沙坪坝区校级期末）如图，在正方形ABCD中，O为对角线AC、BD的交点，E、F分别为边BC、CD上一点，且OE⊥OF，连接EF．若，则EF的长为（　　）

A．2 B．2+ C．+1 D．3
【答案】A
【解答】解：在正方形ABCD中，AC和BD为对角线，
∴∠AOB＝∠BOC＝90°，∠OBC＝∠OCD＝45°，OB＝OC，
∵∠AOE＝150°，
∴∠BOE＝60°；
∵OE⊥OF，
∴∠EOF＝∠BOC＝90°，
∴∠BOE＝∠COF＝60°，
∴△BOE≌△COF（ASA），
∴OE＝OF，
∴△OEF是等腰直角三角形；
过点F作FG⊥OD，如图，

∴∠OGF＝∠DGF＝90°，
∵∠ODC＝45°，
∴△DGF是等腰直角三角形，
∴GF＝DG＝DF＝，
∵∠AOE＝150°，
∴∠BOE＝60°，
∴∠DOF＝30°，
∴OF＝2GF＝，
∴EF＝OF＝2．
故选：A．
5．（秋•乐清市期末）如图，△ABC为等边三角形，以AB为边向形外作△ABD，使∠ADB＝120°，再以点C为旋转中心把△CBD旋转到△CAE，则下列结论：
①D、A、E三点共线；
②DC平分∠BDA；
③∠E＝∠BAC；
④DC＝DB+DA．
其中正确的有（　　）

A．4个 B．3个 C．2个 D．1个
【答案】A
【解答】解：如图，

①设∠1＝x度，则∠2＝（60﹣x）度，∠DBC＝（x+60）度，故∠4＝（x+60）度，
∴∠2+∠3+∠4＝60﹣x+60+x+60＝180度，
∴D、A、E三点共线；
故①正确；
②∵△BCD绕着点C按顺时针方向旋转60°得到△ACE，
∴CD＝CE，∠DCE＝60°，
∴△CDE为等边三角形，
∴∠E＝60°，
∴∠BDC＝∠E＝60°，
∴∠CDA＝120°﹣60°＝60°，
∴DC平分∠BDA；
故②正确；
③∵∠BAC＝60°，
∠E＝60°，
∴∠E＝∠BAC．
故③正确；
④由旋转可知AE＝BD，
又∵∠DAE＝180°，
∴DE＝AE+AD．
∵△CDE为等边三角形，
∴DC＝DB+BA．故④正确；
故选：A．
6．（巴南区校级期末）如图，正方形ABCD，点P是对角线AC上一点，连接BP，过P作PQ⊥BP，PQ交CD于Q，连接BQ交AC于G，若AP＝，Q为CD中点，则下列结论：
①∠PBC＝∠PQD；②BP＝PQ；③∠BPC＝∠BQC；④正方形ABCD的面积是16；
其中正确结论的个数是（　　）

A．4 B．3 C．2 D．1
【答案】A
【解答】解：
∵四边形ABCD是正方形，
∴∠BCQ＝90°，
∵PQ⊥PB，
∴∠BPQ＝90°，
∴∠BPQ+∠BCQ＝180°，
∴B、C、Q、P四点共圆，
∴∠PBC＝∠PQD，∠BPC＝∠BQC，∴①正确；③正确；
过P作PM⊥AD于M，PE⊥AB于E，PF⊥DC于F，则E、P、F三点共线，
∵四边形ABCD是正方形，
∴AB＝AD＝DC＝BC，∠DAC＝∠BAC，∠DAB＝90°，
∴∠MAE＝∠PEA＝∠PMA＝90°，PM＝PE，
∴四边形AMPE是正方形，
∴AM＝PM＝PE＝AE，
∵AP＝，
∴在Rt△AEP中，由勾股定理得：AE2+PE2＝（）2，
解得：AE＝AM＝PE＝PM＝1，
∴DF＝1，
设AB＝BC＝CD＝AD＝a，
则BE＝PF＝a﹣1，
∵∠BEP＝∠PFQ＝∠BPQ＝90°，
∴∠BPE+∠EBP＝90°，∠EPB+∠FPQ＝90°，
∴∠EBP＝∠FPQ，
在△BEP和△PFQ中
，
∴△BEP≌△PFQ（ASA），
∴PE＝FQ＝1，BP＝PQ，∴②正确；
∴DQ＝1+1＝2，
∵Q为CD中点，
∴DC＝2DQ＝4，
∴正方形ABCD的面积是4×4＝16，∴④正确；
故选：A．
7．（2022秋•茂南区期末）如图，在正方形ABCD中，E是边AB的中点，F是边BC的中点，连接CE、DF．求证：CE＝DF．

【解答】证明：∵ABCD是正方形，
∴AB＝BC＝CD，∠EBC＝∠FCD＝90°，
又∵E、F分别是AB、BC的中点，
∴BE＝CF，
在△CEB和△DFC中，
，
∴△CEB≌△DFC，
∴CE＝DF．
8．（2022•碑林区校级开学）如图，在正方形ABCD中，E是边AD的中点，F是CE上点．过点F作GH⊥CE，分别交AB、CD于点G、H，若BG＝1，CH＝5，求AG的长．

【解答】解：过G作GM⊥CD于M，如图：

∵正方形ABCD，
∴∠B＝∠BCD＝∠D＝90°，BC＝CD＝AD，
∵GM⊥CD，
∴四边形GBCM是矩形，
∴GM＝BC＝CD，CM＝BG＝1，∠GMH＝90°＝∠D，
∵GH⊥CF，
∴∠DCE＝90°﹣∠FHM＝∠MGH，
在△GMH和△CDE中，
，
∴△GMH≌△CDE（ASA），
∴HM＝DE，
∵CH＝5，
∴HM＝CH﹣CM＝4＝DE，
∵E是AD边的中点，
∴AB＝AD＝2DE＝8，
∴AG＝AB﹣BG＝8﹣1＝7，
∴AG的长为7．
9．（2022秋•峰峰矿区校级期末）如图，已知四边形ABCD是正方形，对角线AC、BD相交于O，设E、F分别是AD、AB上的点，且∠EOF＝90°．
求证：AE＝BF．

【解答】证明：∵四边形ABCD是正方形，
∴OA＝OB，∠OAE＝∠OBF＝45°，∠AOB＝90°，
∵∠EOF＝90°，
∴∠EOF﹣∠AOF＝∠AOB﹣∠AOF，
即∠AOE＝∠BOF，
在△AOE和△BOF中，
，
∴△AOE≌△BOF（ASA），
∴AE＝BF．
10．（2021秋•莆田期末）如图，点P（3m﹣1，﹣2m+4）在第一象限的角平分线OC上，AP⊥BP，点A在x轴正半轴上，点B在y轴正半轴上．
（1）求点P的坐标．
（2）当∠APB绕点P旋转时，
①OA+OB的值是否发生变化？若变化，求出其变化范围；若不变，求出这个定值．
②请求出OA2+OB2的最小值．

【解答】解：（1）∵点P（3m﹣1，﹣2m+4）在第一象限的角平分线OC上，
∴3m﹣1＝﹣2m+4，
∴m＝1，
∴P（2，2）；
（2）①不变．
过点P作PM⊥y轴于M，PN⊥OA于N．

∵∠PMO＝∠PNO＝∠MON＝90°，PM＝PN＝2，
∴四边形QMPN是正方形，
∴∠MPN＝90°＝∠APB，
∴∠MPB＝∠NPA．
在△PMB和△PNA中，
，
∴△PMB≌△PNA（ASA），
∴BM＝AN，
∴OB+OA＝OM﹣BM+ON+AN＝2OM＝4，
②连接AB，
∵∠AOB＝90°，
∴OA2+OB2＝AB2，
∵∠BPA＝90°，
∴AB2＝PA2+PB2＝2PA2，
∴OA2+OB2＝2PA2，当PA最小时，OA2+OB2也最小．
根据垂线段最短原理，PA最小值为2，
∴OA2+OB2的最小值为8．
11．（2020春•浦东新区期末）已知：四边形ABCD是正方形，对角线AC、BD相交于点O，点E、F分别在边AB、BC上，∠EOF＝90°，如图1
（1）求证：CF＝BE；
（2）如果OG平分∠EOF，与边BC交于点G，如图2，请你猜想BG、CF和GF之间的数量关系，并证明；
（3）设正方形ABCD的边长是2，当点E在AB边上移动时，图2中的△GOF可能是等腰三角形吗？（如果可能，请求出线段BG的长；如果不可能，请说明理由．

【答案】（1） 略 （2）CF2+BG2＝FG2
【解答】证明：（1）如图1，∵四边形ABCD是正方形，

∴OB＝OC，∠OBE＝∠OCF＝45°，AC⊥BD，
∴∠EOF＝∠BOC＝90°，
∴∠EOB＝∠FOC，
在△EOB和△FOC中，
，
∴△EOB≌△FOC（ASA），
∴BE＝CF；
（2）CF2+BG2＝FG2；理由是：
如图2，连接EG，

由（1）知：△EOB≌△FOC，
∴OE＝OF，
∵OG平分∠EOF，
∴∠EOG＝∠FOG，
∵OG＝OG，
∴△EOG≌△FOG（SAS），
∴EG＝FG，
∵四边形ABCD是正方形，
∴∠EBG＝90°，
∴EB2+BG2＝EG2，
∵BE＝CF，
∴CF2+BG2＝FG2；
（3）图2中的△GOF可能是等腰三角形，分三种情况：
①如图3，当OG＝OF时，连接EG，则∠OGF＝∠OFG，
∴∠BGO＝∠CFO，

由（2）知：EG＝FG，
∵OB＝OC，∠OBG＝∠OCF＝45°，
∴△BOG≌△COF（AAS），
∴BG＝CF，
设BG＝x，则BE＝CF＝x，FG＝2﹣2x，
在Rt△BEG中，由勾股定理得：EG2＝BE2+BG2，
（2﹣2x）2＝x2+x2，
x＝2+（舍）或2﹣，
∴BG＝2﹣；
②如图4，OF＝FG时，OE⊥AB，此时E为AB的中点，G与B重合，BG＝0；

③如图5，OG＝FG时，F与C重合，E与B重合，此时BG＝BC＝1；

综上，图2中的△GOF可能是等腰三角形，BG的长为2﹣或0或1．
12．（2022春•长寿区期末）已知：四边形ABCD是正方形．
（1）如图1，点E是边BC的中点，∠AEF＝90°，且EF交正方形外角平分线CF于点F．求证：AE＝EF；
（2）如图2，若把（1）中“点E是边BC的中点”改为“点E是边BC上的任意一点”，其余的条件不变，试证明AE＝EF仍然成立．


【解答】（1）证明：∵点E为BC的中点，
∴BE＝CE，
∵点G为AB的中点，
∴BG＝AG，
∴AG＝CE，
故答案为：AG＝CE；
（2）证明：取AG＝EC，连接EG，

∵四边形ABCD是正方形，
∴AB＝BC，∠B＝90°，
∵AG＝CE，
∴BG＝BE，
∴△BGE是等腰直角三角形，
∴∠BGE＝∠BEG＝45°，
∴∠AGE＝∠ECF＝135°，
∵AE⊥EF，
∴∠AEB+∠FEC＝90°，
∵∠BAE+∠AEB＝90°，
∴∠FEC＝∠BAE，
∴△GAE≌△CEF（ASA），
∴AE＝EF．

13．（2022春•济源期中）在一次课题学习活动中，老师提出了如下问题：如图1，四边形ABCD是正方形，点E是边BC的中点，∠AEF＝90°，且EF交正方形外角平分线CF于点F．请你探究AE与EF存在怎样的数量关系，并证明你的结论正确．
经过探究，小明得出的结论是AE＝EF．而要证明结论AE＝EF，就需要证明AE和EF所在的两个三角形全等，但△ABE和△ECF显然不全等（一个是直角三角形，一个是钝角三角形），考虑到点E是边BC的中点，小明想到的方法是如图2，取AB的中点M，连接EM，证明△AEM≌△EFC．从而得到AE＝EF．
请你参考小明的方法解决下列问题：
（1）如图3，若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”，其余条件不变，证明结论AE＝EF仍然成立．
（2）如图4，若把条件“点E是边BC的中点”改为：“点E是边BC延长线上的一点”，其余条件仍不变，那么结论AE＝EF是否还成立？若成立，请完成证明过程，若不成立，请说明理由．

【解答】（1）证明：如图2，在AB上取点P，连接EP，使AP＝EC，
∵四边形ABCD是正方形，
∴AB＝BC，∠B＝∠BCD＝90°，
∵AP＝EC，
∴BP＝BE，
∴∠BPE＝45°，∠APE＝135°，
∵CF是正方形外角的平分线，
∴∠ECF＝135°，
∵∠AEF＝90°，∠B＝90°，
∴∠BAE＝∠CEF，
在△PAE和△CEF中，
，
∴△PAE≌△CEF，
∴AE＝EF；
（2）证明：延长BA至H，使AH＝CE，连接HE，
∵BA＝BC，AH＝CE，
∴BH＝BE，
∴∠H＝45°，
∵CF是正方形外角的平分线，
∴∠ECF＝45°，
∴∠H＝∠ECF，
∵∠AEF＝90°，∠B＝90°，∠HAE＝∠B+∠BEA，∠CEF＝∠AEF+∠BEA，
∴∠HAE＝∠CEF，
在△HAE和△CEF中，
，
∴△HAE≌△CEF，
∴AE＝EF．
14．（2022春•峡江县期末）如图，在正方形ABCD中，点E、F分别为边BC、CD上两点，∠EAF＝45°，过点A作∠GAB＝∠FAD，且点G为边CB延长线上一点．
（1）△GAB≌△FAD吗？说明理由．
（2）猜想线段DF、BE、EF之间的数量关系并说明理由．


【解答】解：（1）△GAB≌△FAD，理由：
过点A作∠GAB＝∠FAD，且点G为边CB延长线上一点，如图，

∵四边形ABCD为正方形，
∴∠D＝∠ABC＝90°，AB＝AD，
∴∠ABG＝90°，
∴∠ABG＝∠D．
在△GAB和△FAD中，
，
∴△GAB≌△FAD（ASA）；
（2）线段DF、BE、EF之间的数量关系为：DF+BE＝EF．理由：
由（1）知：△GAB≌△FAD，
∴BG＝DF，AG＝AF．
∵∠DAF+∠BAF＝90°，∠GAB＝∠FAD，
∴∠GAB+∠FAB＝90°，
∴∠GAF＝90°．
∵∠EAF＝45°，
∴∠GAE＝∠FAE＝45°．
在△GAE和△FAE中，
，
∴△GAE≌△FAE（SAS），
∴GE＝EF，
∵GE＝BG+BE，
∴DF+BE＝EF．
15．（2022春•雁塔区校级期末）阅读下列材料：
问题：如图（1），已知正方形ABCD中，E、F分别是BC、CD边上的点，且∠EAF＝45°．

解决下列问题：
（1）图（1）中的线段BE、EF、FD之间的数量关系是 　BE+DF＝EF　．
（2）图（2），已知正方形ABCD的边长为8，E、F分别是BC、CD边上的点，且∠EAF＝45°，AG⊥EF于点G，求△EFC的周长．

【解答】解：（1）如图，延长CB至点H使BH等于DF，连接AH．
在△ADF和△ABH中，

∴△ADF≌△ABH（SAS），
∴AF＝AH，∠HAB＝∠FAD，
∵∠BAE+∠FAD＝∠BAD﹣∠EAF＝90°﹣45°＝45°，
∴∠BAE+∠HAB＝∠HAE＝∠EAF＝45°，
在△FAE和△HAE中，

∴△FAE≌△HAE（SAS），
∴EF＝EH，
∵EH＝BH+BE，
∴EF＝FD+BE；
故答案为：EF＝FD+BE．
（2）由（1）可得：∠AEB＝∠AEG，∠AFE＝∠AFD，
在△ABE和△AGE中：
，
∴△ABE≌AGE（AAS），
∴BE＝EG，
在△AGF和△ADF中：
，
∴△AGF≌ADF（AAS），
∴GF＝DF，
∴△EFC的周长＝EG+GF+EC+CF＝BE+EC+DF+CF＝BC+DC＝8+8＝16．


16．（2021秋•兰州期末）如图，在正方形ABCD中，点E、F分别为边BC、CD上两点，∠EAF＝45°，过点A作∠GAB＝∠FAD，且点G为边CB延长线上一点．
①△GAB≌△FAD吗？说明理由．
②若线段DF＝4，BE＝8，求线段EF的长度．
③若DF＝4，CF＝8．求线段EF的长度．

【解答】解：①全等．
证明：∵四边形ABCD为正方形
∴AB＝AD，∠ABG＝∠D，
在△ABG和△ADF中，∠GAB＝∠FAD，AB＝AD，∠ABG＝∠D
∴△GAB≌△FAD．
②解：∵∠BAD＝90°，∠EAF＝45°
∴∠DAF+∠BAE＝45°
∵△GAB≌△FAD
∴∠GAB＝∠FAD，AG＝AF
∴∠GAB+∠BAE＝45°
∴∠GAE＝45°
∴∠GAE＝∠EAF
在△GAE和△FAE中
∵AG＝AF，∠GAE＝∠EAF，AE＝AE
∴△GAE≌△FAE（SAS）
∴EF＝GE．
∵△GAB≌△FAD
∴GB＝DF
∴EF＝GE＝GB+BE＝FD+BE＝8+4＝12．
③设EF＝x，则BE＝GE﹣BG＝x﹣4．
∵EC＝BC﹣BE，
∴EC＝12﹣（x﹣4）＝16﹣x．
在Rt△EFC中，依据勾股定理可知：EF2＝FC2+EC2，即（16﹣x）2+82＝x2，
解得：x＝10．
∴EF＝10．
17．（2021秋•伊通县期末）如图，已知正方形ABCD的边长为6，E，F分别是AB、BC边上的点，且∠EDF＝45°，将△DAE绕点D逆时针旋转90°，得到△DCM．
（1）求证：EF＝MF
（2）若AE＝2，求FC的长．

【解答】解：（1）∵△DAE逆时针旋转90°得到△DCM，
∴∠FCM＝∠FCD+∠DCM＝180°，
∴F、C、M三点共线，
∴DE＝DM，∠EDM＝90°．
∴∠EDF+∠FDM＝90°，
∵∠EDF＝45°，∴∠FDM＝∠EDF＝45°，
∴△DEF≌△DMF（SAS），
∴EF＝MF．

（2）设EF＝MF＝x，
∵AE＝CM＝2，且BC＝6，∴BM＝BC+CM＝6+2＝8，
∴BF＝BM﹣MF＝BM﹣EF＝8﹣x，
∵EB＝AB﹣AE＝6﹣2＝4．
在Rt△EBF中，由勾股定理得EB2+BF2＝EF2．
即42+（8﹣x）2＝x2，
∴解得：x＝5，即FM＝5．
∴FC＝FM﹣CM＝5﹣2＝3．
18．（2021秋•启东市校级月考）（1）如图1，在正方形ABCD中，E、F分别是BC、CD上的点，且∠EAF＝45°，试判断BE、DF与EF三条线段之间的数量关系，直接写出判断结果：　 　．
（2）如图2：在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°．点 E、F分别是BC、CD上的点，且∠EAF＝60°，探究图中线段BE、EF、FD之间的数量关系．请说明理由（提示：延长FD到点C，使DG＝BE，连结AG．）

【解答】解：（1）结论：EF＝BE+DF．理由如下：
如图1，将△ADF绕点A顺时针旋转，使AD与AB重合，得到△ABF′，

∵∠EAF＝45°，
∴∠EAF′＝∠EAF＝45°，
在△AEF和△AEF′中，
，
∴△AEF≌△AEF′（SAS），
∴EF＝EF′，
又EF′＝BE+BF′＝BE+DF，
∴EF＝BE+DF；
故答案为：EF＝BE+DF；
（2）结论：EF＝BE+DF成立．理由如下：
如图2中，延长FD到点G，使DG＝BE，连结AG．
∵∠B＝∠ADC＝90°，
∴∠B＝∠ADG＝90°，
∵AB＝AD，
∴△ABE≌△△ADG（SAS），
∴AE＝AG，∠BAE＝∠DAG，
∵∠BAD＝120°，∠EAF＝60°，
∴∠BAE+∠DAF＝∠EAF＝60°，
∴∠FAG＝∠GAD+∠DAF＝∠BAE+∠DAF＝60°，
∴∠FAE＝∠FAG，
∵AF＝AF，
∴△FAE≌△FAG（SAS），
∴EF＝FG，
∴EF＝FG＝DG+DF＝BE+DF．