【期末满分攻略】2022-2023学年浙教版八年级数学下册讲学案-专题12 特殊平行四边形中的折叠问题（三大类型）

这是一份【期末满分攻略】2022-2023学年浙教版八年级数学下册讲学案-专题12 特殊平行四边形中的折叠问题（三大类型），文件包含期末满分攻略2022-2023学年浙教版八年级数学下册讲学案-专题12特殊平行四边形中的折叠问题三大类型解析版docx、期末满分攻略2022-2023学年浙教版八年级数学下册讲学案-专题12特殊平行四边形中的折叠问题三大类型原卷版docx等2份学案配套教学资源，其中学案共46页， 欢迎下载使用。
模型归纳
专题12 特殊平行四边形中的折叠问题（三大类型）




类型一：矩形中折叠问题
类型二：菱形中折叠问题
解题思路
类型三：正方形中折叠问题

在折叠问题中，原图形与折叠后图形中所隐含的相等线段与相等角常常是解决问题的关键，注意翻折变换的性质的灵活运用，折叠前后，重叠部分是全等形，另外注意勾股定理等知识在求折叠图形的线段长度中的适当运用。
【典例分析】
【类型一：矩形中折叠问题】
【典例1】（2021春•雨花区月考）小西在学完第十八章《平行四边形》之后，研究了新人教版八年级下册数学教材第64页的数学活动1．其内容如下：
如果我们身旁没有量角器或三角尺，又需要作60°，30°，15°等大小的角，可以采用下面的方法（如图1）：（1）对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平．
（2）再次折叠纸片，使点A落在EF上，并使折痕经过点B，得到折痕BM，同时得到了线段BN．
小雅在小西研究的基础上，再次动手操作（如图2）：
（3）将MN延长交BC于点G，将△BMG沿MG折叠，点B刚好落在AD边上点H处，连接GH，把纸片再次展平．请根据小西和小雅的探究，完成下列问题：
①直接写出BE和BN的数量关系：　 　．
②求∠ABM的角度大小；
③求证：四边形BGHM是菱形．

【答案】（3）①BE＝BN ② ∠ABM＝30 ③四边形BGHM是菱形
【解答】解：（3）①∵对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，
∴BE＝AB，
∵再次折叠纸片，使点A落在EF上，并使折痕经过点B，得到折痕BM，同时得到了线段BN．
∴AB＝BN，
∴BE＝BN，
故答案为：BE＝BN；
②解：∵由折叠的性质得：∠BEN＝∠AEN＝90°，
∵BE＝BN，
∴∠BNE＝30°，
∴∠ABN＝60°，
由折叠的性质得：∠ABM＝∠ABN＝30°；
③证明：由②得∠ABM＝30°，
∵四边形ABCD是矩形，
∴∠A＝∠ABC＝90°，
∴∠AMB＝∠BMN＝60°，∠MBG＝60°，
∴△BMG是等边三角形，
∴BM＝BG，
由折叠得BM＝MH，BG＝GH，
∴BM＝MH＝BG＝GH，
∴四边形BGHM是菱形．
【变式1-1】（2021•黔西南州）如图，在矩形纸片ABCD中，AB＝6，BC＝9，M是BC上的点，且CM＝3，将矩形纸片ABCD沿过点M的直线折叠，使点D落在AB上的点P处，点C落在点C′处，折痕为MN，则线段AN的长是 　　．

【答案】4
【解答】解：连接PM，如图
∵AB＝6，BC＝9，CM＝3，
∴BM＝BC﹣CM＝9﹣3＝6，
由折叠性质得，CD＝PC′＝6，∠C＝∠PC′M＝∠PBM＝90°，C′M＝CM＝3，
在Rt△PBM和Rt△MC′P中，
，
∴Rt△PBM≌Rt△MC′P（HL），
∴PB＝C′M＝3，
∴PA＝AB﹣PB＝6﹣3＝3．
设AN＝x，则ND＝9﹣x＝PN，
在Rt△APN中，AN2+AP2＝PN2，
即x2+32＝（9﹣x）2，
解得x＝4，
∴AN的长是4．
故答案为4．

【变式1-2】（2021•徐州）如图，将一张长方形纸片ABCD沿EF折叠，使 C、A两点重合，点D落在点G处．已知AB＝4，BC＝8．
（1）求证：△AEF是等腰三角形；
（2）求线段FD的长．

【答案】（1） 略 （2）FD＝3
【解答】（1）证明：由折叠性质可知，∠AEF＝∠CEF，
由矩形性质可得AD∥BC，
∴∠AFE＝∠CEF，
∴∠AEF＝∠AFE．
∴AE＝AF，
故△AEF为等腰三角形．
（2）解：由折叠可得AE＝CE，设CE＝x＝AE，
则BE＝BC﹣CE＝8﹣x，
∵∠B＝90°，
在Rt△ABE中，有AB2+BE2＝AE2，
即42+（8﹣x）2＝x2，解得：x＝5．
由（1）结论可得AF＝AE＝5，
故FD＝AD﹣AF＝BC﹣AF＝8﹣5＝3．


【类型二：菱形中折叠问题】
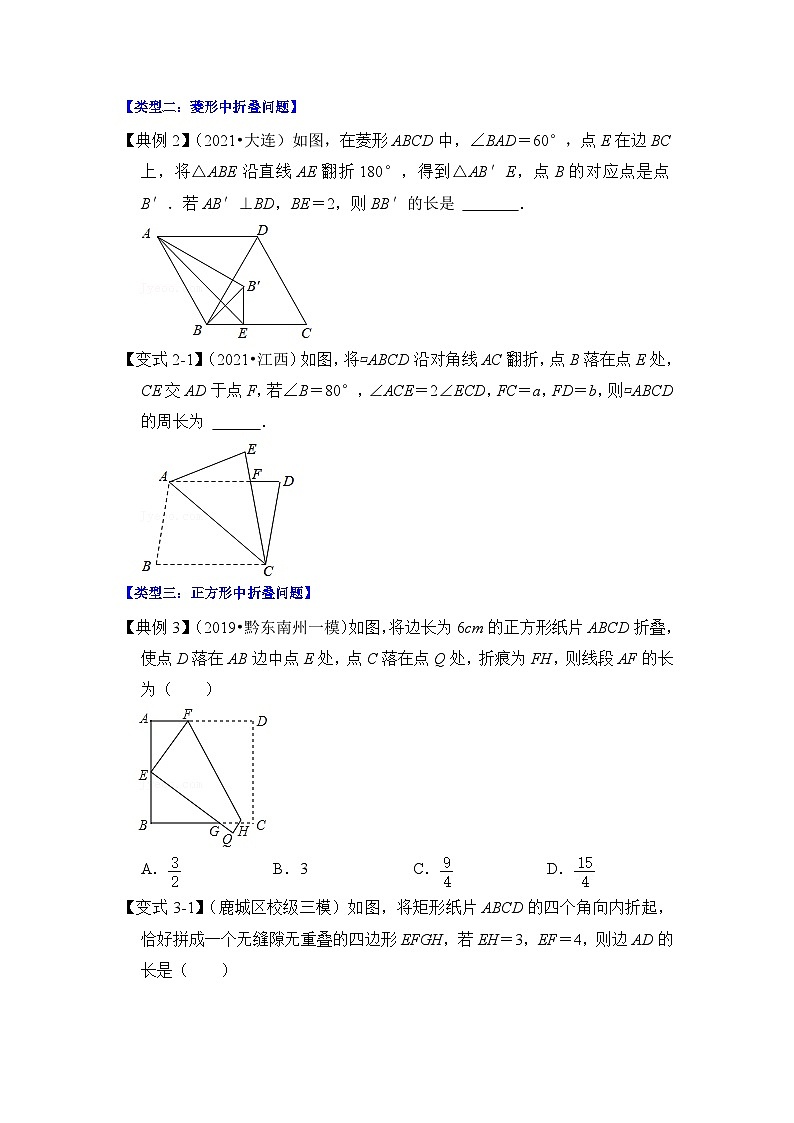
【典例2】（2021•大连）如图，在菱形ABCD中，∠BAD＝60°，点E在边BC上，将△ABE沿直线AE翻折180°，得到△AB′E，点B的对应点是点B′．若AB′⊥BD，BE＝2，则BB′的长是 　 　．

【答案】2
【解答】解：∵菱形ABCD，
∴AB＝AD，AD∥BC，
∵∠BAD＝60°，
∴∠ABC＝120°，
∵AB′⊥BD，
∴∠BAB'＝，
∵将△ABE沿直线AE翻折180°，得到△AB′E，
∴BE＝B'E，AB＝AB'，
∴∠ABB'＝，
∴∠EBB'＝∠ABE﹣∠ABB'＝120°﹣75°＝45°，
∴∠EB'B＝∠EBB'＝45°，
∴∠BEB'＝90°，
在Rt△BEB'中，由勾股定理得：
BB'＝，
故答案为：2．
【变式2-1】（2021•江西）如图，将▱ABCD沿对角线AC翻折，点B落在点E处，CE交AD于点F，若∠B＝80°，∠ACE＝2∠ECD，FC＝a，FD＝b，则▱ABCD的周长为 　 　．

【答案】4a+2b
【解答】解：∵∠B＝80°，四边形ABCD为平行四边形．
∴∠D＝80°．
由折叠可知∠ACB＝∠ACE，
又AD∥BC，
∴∠DAC＝∠ACB，
∴∠ACE＝∠DAC，
∴△AFC为等腰三角形．
∴AF＝FC＝a．
设∠ECD＝x，则∠ACE＝2x，
∴∠DAC＝2x，
在△ADC中，由三角形内角和定理可知，2x+2x+x+80°＝180°，
解得：x＝20°．
∴由三角形外角定理可得∠DFC＝4x＝80°，
故△DFC为等腰三角形．
∴DC＝FC＝a．
∴AD＝AF+FD＝a+b，
故平行四边形ABCD的周长为2（DC+AD）＝2（a+a+b）＝4a+2b．
故答案为：4a+2b．


【类型三：正方形中折叠问题】
【典例3】（2019•黔东南州一模）如图，将边长为6cm的正方形纸片ABCD折叠，使点D落在AB边中点E处，点C落在点Q处，折痕为FH，则线段AF的长为（　　）

A． B．3 C． D．
【答案】C
【解答】解：∵将边长为6cm的正方形纸片ABCD折叠，使点D落在AB边中点E处，
∴EF＝DE，AB＝AD＝6cm，∠A＝90°
∵点E是AB的中点，
∴AE＝BE＝3cm，
在Rt△AEF中，EF2＝AF2+AE2，
∴（6﹣AF）2＝AF2+9
∴AF＝
故选：C．
【变式3-1】（鹿城区校级三模）如图，将矩形纸片ABCD的四个角向内折起，恰好拼成一个无缝隙无重叠的四边形EFGH，若EH＝3，EF＝4，则边AD的长是（　　）

A．2 B．3 C．4.8 D．5
【答案】D
【解答】解：∵∠HEM＝∠AEH，∠BEF＝∠FEM，
∴∠HEF＝∠HEM+∠FEM＝×180°＝90°，
同理可得：∠EHG＝∠HGF＝∠EFG＝90°，
∴四边形EFGH为矩形．
∵AD＝AH+HD＝HM+MF＝HF，HF＝＝5，
∴AD＝5，
故选：D．
【变式3-2】（2021•牡丹江）如图，正方形ABCD的边长为3，E为BC边上一点，BE＝1．将正方形沿GF折叠，使点A恰好与点E重合，连接AF，EF，GE，则四边形AGEF的面积为（　　）

A．2 B．2 C．6 D．5
【答案】D
【解答】解：设DF＝m，AG＝n，
∵正方形的边长为3，
∴CF＝3﹣m，BG＝3﹣n，
由折叠可得，AF＝EF，AG＝GE，
在Rt△ADF中，AF2＝DF2+DA2，
即AF2＝m2+9，
在Rt△EFC中，EF2＝EC2+CF2，
∵BE＝1，
∴EC＝2，
∴EF2＝4+（3﹣m）2，
∴m2+9＝4+（3﹣m）2，
∴m＝，
在Rt△BEG中，GE2＝BG2+BE2，
∴n2＝（3﹣n）2+1，
∴n＝，
∴S△GEB＝×1×（3﹣）＝，
S△ADF＝××3＝1，
S△CEF＝×2×（3﹣）＝，
∴S四边形AGEF＝S正方形ABCD﹣S△GEB﹣S△ADF﹣S△CEF＝9﹣﹣1﹣＝5，
故选：D．

【夯实基础】
1．长方形纸片对边是互相平行的．将其折叠成如图所示的图形，若∠ABC＝64°，则∠CAB的度数是（　　）

A．53° B．58° C．63° D．68°
【答案】B
【解答】解：如图所示，

∵AB∥DE．
∴∠BCD＝∠ABC＝64°．
∵∠BCD+∠BCE＝180°．
∴∠BCE＝116°．
由折叠性质可知，∠ACE＝∠ACB．
∴∠ACE＝∠BCE＝58°．
∵AB∥CE．
∴∠CAB＝∠ACE＝58°．
故选：B．
2．如图，AC为矩形ABCD的对角线，将边AB沿AE折叠，使点B落在AC上的点M处，将边CD沿CF折叠，使点D落在AC上的点N处，易证四边形AECF是平行四边形．要使四边形AECF是菱形，则∠BAE的度数是（　　）

A．30° B．40° C．45° D．50°
【答案】A
【解答】解：由折叠的性质得：∠BAE＝∠CAE，
∵四边形ABCD是矩形，
∴∠BAD＝90°，AD∥BC，
∴∠DAC＝∠ACE，
∵四边形AECF是菱形，
∴AE＝CE，
∴∠CAE＝∠ACE，
∴∠BAE＝∠CAE＝∠DAC，
∴∠BAE＝×90°＝30°，
故选：A．
3．如图，将长方形纸片折叠，使A点落在BC上的F处，折痕为BE，若沿EF剪下，则折叠部分是一个正方形，其数学原理是（　　）

A．邻边相等的矩形是正方形
B．对角线相等的菱形是正方形
C．两个全等的直角三角形构成正方形
D．轴对称图形是正方形
【答案】A
【解答】解：∵将长方形纸片折叠，A落在BC上的F处，
∴BA＝BF，
∵折痕为BE，沿EF剪下，
∴四边形ABFE为矩形，
∴四边形ABEF为正方形．
故用的判定定理是：邻边相等的矩形是正方形．
故选：A．
4．如图，在菱形纸片ABCD中，∠A＝60°，点E在BC边上，将菱形纸片ABCD沿DE折叠，点C对应点为点C′，且DC′是AB的垂直平分线，则∠DEC的大小为（　　）

A．30° B．45° C．60° D．75°
【答案】D
【解答】解：连接BD，如图所示：
∵四边形ABCD为菱形，
∴AB＝AD，
∵∠A＝60°，
∴△ABD为等边三角形，∠ADC＝120°，∠C＝60°，
∵DC′是AB的垂直平分线，
∴P为AB的中点，
∴DP为∠ADB的平分线，即∠ADP＝∠BDP＝30°，
∴∠PDC＝90°，
∴由折叠的性质得到∠CDE＝∠PDE＝45°，
在△DEC中，∠DEC＝180°﹣（∠CDE+∠C）＝75°．
故选：D．

5．将矩形纸片ABCD按如图所示的方式折叠，恰好得到菱形AECF．若AB＝3，则菱形AECF的面积为（　　）

A．1 B．2 C．2 D．4
【答案】C
【解答】解：∵四边形AECF是菱形，AB＝3，
∴假设BE＝x，则AE＝3﹣x，CE＝3﹣x，
∵四边形AECF是菱形，
∴∠FCO＝∠ECO，
∵∠ECO＝∠ECB，
∴∠ECO＝∠ECB＝∠FCO＝30°，
2BE＝CE，
∴CE＝2x，
∴2x＝3﹣x，
解得：x＝1，
∴CE＝2，利用勾股定理得出：
BC2+BE2＝EC2，
BC＝＝＝，
又∵AE＝AB﹣BE＝3﹣1＝2，
则菱形的面积是：AE•BC＝2．
故选：C．

6．如图，点E是矩形ABCD中CD边上一点，将△BCE沿BE折叠为△BFE，点F落在边AD上，若∠AFB＝50°，则∠DFE＝　 　．

【答案】40°
【解答】解：∵四边形ABCD是矩形，
∴∠C＝90°，
由翻折可知：∠EFB＝∠C＝90°，
∴∠AFB+∠DFE＝90°，
∵∠AFB＝50°，
∴∠DFE＝40°．
故答案为：40°．
7．如图，一张矩形纸片，按照下面步骤进行折叠：
第一步，在矩形纸片的一端，利用图①的方法折出一个正方形，然后把纸片展平．
第二步，如图②，把这个正方形折成两个相等的矩形，再把纸片展平．
第三步，折出内侧矩形的对角线AB，并把AB折到图③中所示的AD处．
第四步，展平纸片，按照所得的点D折出DE，得出矩形BCDE（图④）．则矩形BCDE的宽与长的比为 　 　．


【答案】
【解答】解：设BC＝NC＝MN＝2a，
∵把这个正方形折成两个相等的矩形，
∴NA＝AC＝a，
∴AB＝＝a，
∵并把AB折到图③中所示的AD处．
∴AD＝AB＝a，
∴CD＝（﹣1）a，
∴矩形BCDE的宽与长的比＝，
故答案为：．
8．如图，把一张长方形的纸条按图那样折叠后，B、C两点落在B′、C′点处，若得∠B′OG＝56°，则∠AOB′余角的度数为 　 　．

【答案】22°
【解答】解：∵把一张长方形的纸条按图那样折叠后，
∴∠B'OG＝∠BOG＝56°，
∴∠AOB'＝68°，
∴∠AOB′余角的度数为22°，
故答案为：22°．
9．如图，把长方形纸片OABC放入平面直角坐标系中，使OA，OC分别落在x轴、y轴上，连接AC，将纸片OABC沿AC折叠，使点B落在点D的位置，AD与y轴交于点E，若B（2，4），则OE的长为　 　．

【答案】
【解答】解：∵四边形OABC是矩形，
∴OC∥AB，
∴∠ECA＝∠CAB，
根据题意得：∠CAB＝∠CAD，∠CDA＝∠B＝90°，
∴∠ECA＝∠EAC，
∴EC＝EA，
∵B（2，4），
∴AD＝AB＝4，
设OE＝x，则AE＝EC＝OC﹣OE＝4﹣x，
在Rt△AOE中，AE2＝OE2+OA2，
即（4﹣x）2＝x2+4，
解得：x＝，
∴OE＝，
故答案为：．
10．已知四边形ABCD，其中AD∥BC，AB⊥BC，将DC沿DE折叠，C落于C'，DC'交CB于G，且ABGD为长方形（如图1）；再将纸片展开，将AD沿DF折叠，使A点落在DC上一点A'（如图2），在两次折叠过程中，两条折痕DE、DF所成的角为　 　度．

【答案】45
【解答】解：设∠EDC＝x，∠GDF＝y，
由折叠性质可知，∠EDG＝x，∠ADF＝∠CDF＝2x+y，
由∠ADG＝90°，得2x+y+y＝90°，
∴x+y＝45°，
故∠EDF＝x+y＝45°，
故答案为：45．

11．如图1，在一张长方形纸片ABCD上画一条线段MN，将纸片沿线段MN折叠（如图2），当∠1＝70°时，∠KNC＝ （注：长方形纸片对边平行，即：CD∥AB，AD∥BC）．

【答案】　40°　
【解答】解：∵AB∥CD，
∴∠MNK＝∠1＝70°，
由折叠的性质可得：∠1＝∠NMK＝70°，
∵CN∥BM，
∴∠CNM+∠KMN＝180°，
∴∠CNM＝110°，
∴∠KNC＝40°，
故答案为：40°．
12．如图，在矩形纸片ABCD中，边AB＝12，AD＝5，点P为DC边上的动点（点P不与点D，C重合），将纸片沿AP折叠，则CD′的最小值为　 　．

【答案】8
【解答】解：连接AC，当点D'在AC上时，CD'有最小值，

∵四边形ABCD是矩形，AB＝12，AD＝5，
∴∠D＝∠B＝90°，AD＝BC，
∴AC＝，
由折叠性质得：AD＝AD'＝5，∠AD'P＝∠D＝90°，
∴CD'的最小值＝AC﹣AD'＝13﹣5＝8，
故答案为：8．
13．将长方形ABCD纸片按如图所示的方式折叠，EF，BG为折痕，那么，∠AEF+∠BEG＝　 　．

【答案】90°
【解答】解：由折叠可知：∠AEF＝∠FEA1，∠BEG＝∠GEA1，
∵∠AEF+∠FEA1+∠BEG+∠GEA1＝180°，
∴∠AEF+∠BEG＝90°．
故答案为：90°．
14．如图，在平面直角坐标系中，矩形ABCO的边CO、OA分别在x轴、y轴上，点E在边BC上，将该矩形沿AE折叠，点B恰好落在边OC上的F处．若OA＝6，AB＝10，则点E的坐标是 　 　．

【答案】（10，）
【解答】解：设CE＝a，则BE＝6﹣a，
由题意可得，EF＝BE＝6﹣a，
由对折知，AF＝AB＝10，
∴，
∴CF＝OC﹣OF＝10﹣8＝2，
∵∠ECF＝90°，
∴a2+22＝（6﹣a）2，
解得，a＝，
∴点E的坐标为（10，），
故答案为（10，）．

15．如图，在Rt△ABC中，∠ACB＝90°，将边BC沿斜边上的中线CD折叠到CB′，若∠B＝50°，则∠ACB′＝　 　．

【答案】10°
【解答】解：∵∠ACB＝90°，∠B＝50°，
∴∠A＝40°，
∵∠ACB＝90°，CD是斜边上的中线，
∴CD＝BD，CD＝AD，
∴∠BCD＝∠B＝50°，∠DCA＝∠A＝40°，
由翻折变换的性质可知，∠B′CD＝∠BCD＝50°，
∴∠ACB′＝∠B′CD﹣∠DCA＝10°，
故答案为：10°．
16．如图，一张半透明的矩形纸片上有一点P，将纸片按如图所示的方法经两次折叠周开（先过点P折叠，使得图中给出的一条线段在折叠后重合，再用同样的方法折叠，使得第一次折叠得到的折痕在折叠后重合），若∠1＝28°，则∠2＝　 　．


【答案】152°
【解答】解：如图所示，根据折叠的性质可得：PE⊥DF，PE⊥BC，

∴∠APB＝∠DQE＝90°，
∴∠1+∠PAB＝90°，
∴∠PAB＝90°﹣∠1＝62°，
∵该纸片为矩形，
∴AB∥DE，
∴∠DEQ＝∠PAB＝62°，
∴∠2＝∠DQE+∠DEQ＝90°+62°＝152°，
故答案为：152°．
17．（2021•黔东南州模拟）如图，矩形纸片ABCD中，已知AD＝8，折叠纸片使AB边与对角线AC重合，点B落在点F处，折痕为AE，且EF＝3，则AB的长为　　．

【答案】6
【解答】解：∵四边形ABCD是矩形，AD＝8，
∴BC＝8，
∵△AEF是△AEB翻折而成，
∴BE＝EF＝3，AB＝AF，△CEF是直角三角形，
∴CE＝8﹣3＝5，
在Rt△CEF中，CF＝＝＝4，
设AB＝x，
在Rt△ABC中，AC2＝AB2+BC2，即（x+4）2＝x2+82，
解得x＝6，则AB＝6．
故答案为：6．
18．（2020•广东）如图，矩形ABCD中，AB＞AD，把矩形沿对角线AC所在直线折叠，使点B落在点E处，AE交CD于点F，连接DE．
（1）求证：△ADE≌△CED；
（2）求证：△DEF是等腰三角形．

【答案】（1）略 （2）略
【解答】证明：（1）∵四边形ABCD是矩形，
∴AD＝BC，AB＝CD．
由折叠的性质可得：BC＝CE，AB＝AE，
∴AD＝CE，AE＝CD．
在△ADE和△CED中，，
∴△ADE≌△CED（SSS）．
（2）由（1）得△ADE≌△CED，
∴∠DEA＝∠EDC，即∠DEF＝∠EDF，
∴EF＝DF，
∴△DEF是等腰三角形．

19．（2020•兴化市模拟）如图，现有一张矩形纸片ABCD，AB＝4，BC＝8，点M，N分别在矩形的边AD，BC上，将矩形纸片沿直线MN折叠，使点C落在矩形的边AD上，记为点P，点D落在G处，连接PC，交MN丁点Q，连接CM．
（1）求证：PM＝PN；
（2）当P，A重合时，求MN的值；
（3）若△PQM的面积为S，求S的取值范围．

【答案】（1） 略 （2）MN＝2QN＝2 （3）4≤S≤5
【解答】（1）证明：如图1中，

∵四边形ABCD是矩形，
∴PM∥CN，
∴∠PMN＝∠MNC，
∵∠MNC＝∠PNM，
∴∠PMN＝∠PNM，
∴PM＝PN．
（2）解：点P与点A重合时，如图2中，

设BN＝x，则AN＝NC＝8﹣x，
在Rt△ABN中，AB2+BN2＝AN2，
即42+x2＝（8﹣x）2，
解得x＝3，
∴CN＝8﹣3＝5，AC＝＝＝4，
∴CQ＝AC＝2，
∴QN＝＝＝，
∴MN＝2QN＝2．

（3）解：当MN过点D时，如图3所示，

此时，CN最短，四边形CMPN的面积最小，则S最小为S＝S菱形CMPN＝×4×4＝4，
当P点与A点重合时，CN最长，四边形CMPN的面积最大，则S最大为S＝×5×4＝5，
∴4≤S≤5，

20．（1）将矩形纸片ABCD沿过点D的直线折叠，使点A落在CD上的点A'处，得到折痕DE，如图1．求证：四边形AEA'D是正方形；
（2）将图1中的矩形纸片ABCD沿过点E的直线折叠，点C恰好落在AD上的点C'处，点B落在点B'处，得到折痕EF，B'C'交AB于点M，如图2．线段MC'与ME是否相等？若相等，请给出证明；若不等，请说明理由．

【解答】（1）证明：∵ABCD是矩形，
∴∠A＝∠ADC＝90°，
∵将矩形纸片ABCD沿过点D的直线折叠，使点A落在CD上的点A'处，得到折痕DE，
∴AD＝A′D，AE＝A′E，∠ADE＝∠A′DE＝45°，
∵AB∥CD，
∴∠AED＝∠A′DE＝∠ADE，
∴AD＝AE，
∴AD＝AE＝A′E＝A′D，
∴四边形AEA′D是菱形，
∵∠A＝90°，
∴四边形AEA′D是正方形；
（2）解：MC′＝ME．
证明：如图1，连接C′E，由（1）知，AD＝AE，

∵四边形ABCD是矩形，
∴AD＝BC，∠EAC′＝∠B＝90°，
由折叠知，B′C′＝BC，∠B＝∠B′，
∴AE＝B′C′，∠EAC′＝∠B′，
又EC′＝C′E，
在Rt△EC′A和Rt△C′EB′中，
，
∴Rt△EC′A≌Rt△C′EB′（HL），
∴∠C′EA＝∠EC′B′，
∴MC′＝ME．
21．小明尝试着将矩形纸片ABCD（如图①，AD＞CD）沿过A点的直线折叠，使得B点落在AD边上的点F处，折痕为AE（如图②）；再沿过D点的直线折叠，使得C点落在DA边上的点N处，E点落在AE边上的点M处，折痕为DG（如图③）．如果第二次折叠后，M点正好在∠NDG的平分线上，求矩形ABCD长与宽的比值．

【解答】解：连接DE，如图：

∵沿过A点的直线折叠，使得B点落在AD边上的点F处，
∴四边形ABEF为正方形，
∴∠EAD＝45°，
由第二次折叠知，M点正好在∠NDG的平分线上，
∴DE平分∠GDC，
∴∠GDE＝∠CDE，
∵DG为折痕，
∴∠DGE＝90°＝∠C，
而DE＝DE，
∴Rt△DGE≌Rt△DCE（AAS），
∴DC＝DG，
∵∠EAD＝45°，∠DGA＝90°，
∴△AGD为等腰直角三角形，
∴AD＝DG＝CD，
∴矩形ABCD长与宽的比值为，
故答案为．
22．如果我们身旁没有量角器或三角尺，又需要作60°，30°，15°等大小的角，可以采用下面的方法如图1：
第一步：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展开如图1．
第二步：再一次折叠纸片，使点A落在EF上，并使折痕经过点B，得到折痕BM，同时，得到了线段BN如图2．

（1）求∠NBC的度数；
（2）通过以上折纸操作，还得到了一些不同角度的角，请写出除∠NBC以外的两个角及它们的度数；
（3）请你继续折出15°大小的角，说出折纸步骤及得到的15°角．
【解答】解：（1）如图，连接AN，

由折叠可得：AB＝NB，EF垂直平分AB，
∴NA＝NB，
∴AB＝NA＝NB，
∴△ABN为等边三角形，
∴∠ABN＝60°，
∵四边形ABCD为矩形，
∴∠ABC＝90°，
∠NBC＝∠ABC﹣∠NBC＝90°﹣60°＝30°；
（2）由折叠可知：∠ABM＝∠NBM＝∠ABN＝×60°＝30°，
∵∠BAD＝90°，
∴∠AMB＝60°；
（3）如图所示，

再一次折叠纸片，使点A落在BM上，并使折痕经过点B，得到折痕BH，则∠ABH＝15°．
23．一张矩形纸ABCD，将点B翻折到对角线AC上的点M处，折痕CE交AB于点E．将点D翻折到对角线AC上的点H处，折痕AF交DC于点F，折叠出四边形AECF．
（1）求证：AF∥CE；
（2）当∠BAC＝　30　度时，四边形AECF是菱形？说明理由．

【解答】（1）证明：∵四边形ABCD为矩形，
∴AD∥BC，
∴∠DAC＝∠BCA，
由翻折知，∠DAF＝∠HAF＝∠DAC，∠BCE＝∠MCE＝∠BCA，
∴∠HAF＝∠MCE，
∴AF∥CE；
（2）解：当∠BAC＝30°时四边形AECF为菱形，理由如下：
∵四边形ABCD是矩形，
∴∠D＝∠BAD＝90°，AB∥CD，
由（1）得：AF∥CE，
∴四边形AECF是平行四边形，
∵∠BAC＝30°，
∴∠DAC＝60°．
∴∠ACD＝30°，
由折叠的性质得∠DAF＝∠HAF＝30°，
∴∠HAF＝∠ACD，
∴AF＝CF，
∴四边形AECF是菱形；
故答案为：30．
24．如图，矩形ABCO中，点C在x轴上，点A在y轴上，点B的坐标是（﹣6，8）．矩形ABCO沿直线BD折叠，使得点A落在对角线OB上的点E处，折痕与OA、x轴分别交于点D、F．
（1）求点D的坐标；
（2）若点N是平面内任一点，在x轴上是否存在点M，使M、N、E、O为顶点的四边形是菱形？若存在，请直接写出满足条件的点M的坐标；若不存在，请说明理由．

【解答】解：（1）∵四边形ABCO是矩形，点B的坐标是（﹣6，8）．
∴∠BAD＝∠OCB＝90°，AB＝OC＝6，OA＝BC＝8，
∴BO＝＝10；
由折叠的性质得：BE＝AB＝6，∠BED＝∠BAD＝90°，DE＝AD，
∴OE＝BO﹣BE＝10﹣6＝4，∠OED＝90°，
设D（0，a），则OD＝a，DE＝AD＝OA﹣OD＝8﹣a，
在Rt△EOD中，由勾股定理得：DE2+OE2＝OD2，
即（8﹣a）2+42＝a2，解得：a＝5，
∴D（0，5）；

（2）存在，点M的坐标为（4，0）或（﹣4，0）或（﹣，0）或（﹣，0）；理由如下：
①当OM、OE都为菱形的边时，OM＝OE＝4，
∴M的坐标为（4，0）或（﹣4，0）；
②当OM为菱形的边，OE为对角线时，MN垂直平分OE，垂足为G，如图1所示：
则OG＝OE＝2，
∵OA＝8，OD＝5，
∴AD＝DE＝3，
∴E到y轴的距离＝＝＝，
∴OH＝，
∵EM2﹣MH2＝42﹣（）2，
∴OM2﹣（OM﹣）2＝42﹣（）2，
解得：OM＝，
∴M（﹣，0）；
③当OM为菱形的对角线，OE为边时，如图2所示：
同②得：M（﹣，0）；
综上所述，在x轴上存在点M，使以M、N、E、O为顶点的四边形是菱形，点M的坐标为（4，0）或（﹣4，0）或（﹣，0）或（﹣，0）．


25.．如图，AC为矩形ABCD的对角线，将边AB沿AE折叠，使点B落在AC上的点M处，将边CD沿CF折叠，使点D落在AC上的点N处．
（1）求证：四边形AECF是平行四边形；
（2）当∠BAE为多少度时，四边形AECF是菱形？请说明理由．

【解答】解：（1）方法一：∵四边形ABCD为矩形，
∴AB＝CD，AD∥BC，∠B＝∠D＝90°，∠BAC＝∠DCA．
由翻折的性质可知：∠EAC＝∠BAC，∠NCF＝∠DCA
∴∠EAC＝∠NCF，
∴AE∥CF，
∵AF∥EC，
∴四边形AECF是平行四边形；
方法二：∵四边形ABCD为矩形，
∴AB＝CD，AD∥BC，∠B＝∠D＝90°，∠BAC＝∠DCA．
由翻折的性质可知：∠EAB＝∠BAC，∠DCF＝∠DCA．
∴∠EAB＝∠DCF．
在△ABE和△CDF中，
∴△ABE≌△CDF（ASA），
∴DF＝BE．
∴AF＝EC．
又∵AF∥EC，
∴四边形AECF是平行四边形；
（2）当∠BAE＝30°时，四边形AECF是菱形，
理由：由折叠可知，∠BAE＝∠CAE＝30°，
∵∠B＝90°，
∴∠ACE＝90°﹣60°＝30°，
即∠CAE＝∠ACE，
∴EA＝EC，
∵四边形AECF是平行四边形，
∴四边形AECF是菱形．
26．已知矩形纸片OBCD的边OB在x轴上，OD在y轴上，点C在第一象限，且OB＝8，OD＝6．现将纸片折叠，折痕为EF （点E、F是折痕与矩形的边的交点），点P为点D的对应点，再将纸片还原．
（Ⅰ）若点P落在矩形OBCD的边OB上，
①如图①，当点E与点O重合时，求点F的坐标；
②如图②，当点E在OB上，点F在DC上时，EF与DP交于点G，若OP＝7，求点F的坐标；
（Ⅱ）若点P落在矩形OBCD的内部，且点E，F分别在边OD，边DC上，当OP取最小值时，求点P的坐标（直接写出结果即可）．

【解答】解：（Ⅰ）①∵折痕为EF，点P为点D的对应点，
∴△DOF≌△POF．
∴∠DOF＝∠POF＝45°．
∵四边形OBCD是矩形，
∴∠ODF＝90°．
∴∠DFO＝∠DOF＝45°．
∴DF＝DO＝6．
∴点F的坐标为（6，6）；
②∵折痕为EF，点P为点D的对应点，
∴DG＝PG，EF⊥PD．
∵四边形OBCD是矩形，
∴DC∥OB，
∴∠FDG＝∠EPG．
∵∠DGF＝∠PGE，
∴△DGF≌△PGE（ASA）．
∴DF＝PE．
∵DF∥PE，
∴四边形DEPF是平行四边形．
∵EF⊥PD，
∴▱DEPF是菱形，
设菱形的边长为x，则DE＝EP＝x．
∵OP＝7，
∴OE＝7﹣x，
在Rt△ODE中，由勾股定理得OD2+OE2＝DE2．
∴62+（7﹣x）2＝x2，
解得．
∴，
∴点F的坐标为（，6）；