2020北京四十三中学初一（上）期中数学（教师版）

这是一份2020北京四十三中学初一（上）期中数学（教师版），共17页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

2020北京四十三中学初一（上）期中
数 学
学校:___________姓名：___________班级：___________考号：___________
一、单选题
1．数学文化《九章算术》中注有“今两算得失相反，要令正负以名之”，意思是：今有两数，若其意义相反，则分别叫做正数与负数．若向东走9米记作米，则米表示（ ）
A．向东走5米 B．向西走5米 C．向东走4米 D．向两走4米
2．截止到3月26日0时，全球感染新型冠状病毒肺炎的人数已经突破380000人，“山川异域，风月同天”，携手抗“疫”，刻不容缓．将380000用科学记数法表示为（　　）
A．0.38×106 B．3.8×106 C．3.8×105 D．38×104
3．下列关于0的说法错误的是（ ）
A．任何情况下，0的实际意义就是什么都没有 B．0是偶数不是奇数
C．0不是正数也不是负数 D．0是整数也是有理数
4．有理数a，b在数轴上的位置如图所示，下列各式成立的是(　　)

A．b＞0 B．|a|＞－b C．a＋b＞0 D．ab＜0
5．下列各组数中，互为相反数的是（ ）
A．与 B．与 C．与 D．8与
6．如果a＋b0，并且ab0，那么(　　)
A．a0，b0 B．a0，b0
C．a0，b0 D．a0，b0
7．下列说法中正确的是（　　）
A．是单项式 B．﹣πx的系数为﹣1
C．﹣5不是单项式 D．﹣5a2b的次数是3
8．下列各组数中，不是同类项的是（ ）
A．-10和23 B．-m2n与-2nm2 C．xy2z和xyz2 D．与-2a
9．下列说法中，正确的是（ ）
A．a2 + 1一定是正数 B．绝对值小于的整数是1和-1
C．绝对值最小的有理数是1 D．倒数是它本身的数是1，-1和0
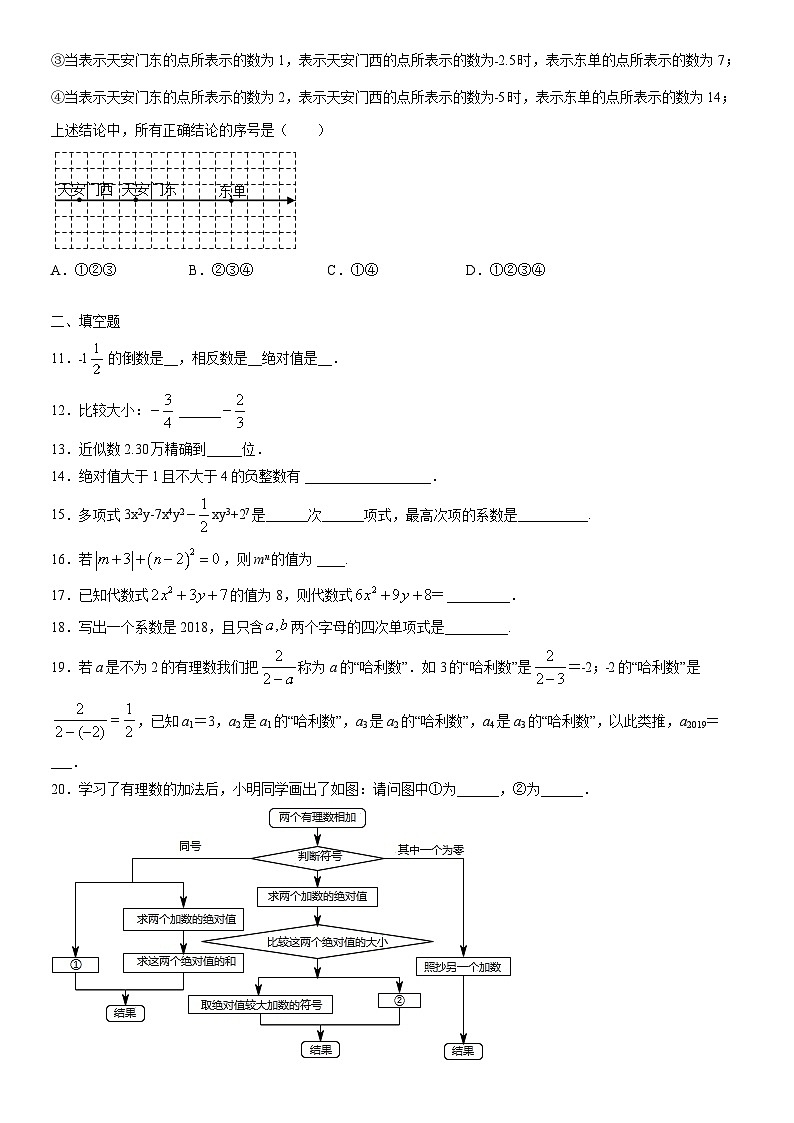
10．如图是北京地铁一号线部分站点的分布示意图，在图中以正东为正方向建立数轴，有如下四个结论：
①当表示天安门东的点所表示的数为0，表示天安门西的点所表示的数为﹣3.5时，表示东单的点所表示的数为6；
②当表示天安门东的点所表示的数为0，表示天安门西的点所表示的数为﹣7时，表示东单的点所表示的数为12；
③当表示天安门东的点所表示的数为1，表示天安门西的点所表示的数为﹣2.5时，表示东单的点所表示的数为7；
④当表示天安门东的点所表示的数为2，表示天安门西的点所表示的数为﹣5时，表示东单的点所表示的数为14；
上述结论中，所有正确结论的序号是（　　）

A．①②③ B．②③④ C．①④ D．①②③④

二、填空题
11．﹣1的倒数是__，相反数是__绝对值是__．
12．比较大小： ______
13．近似数2.30万精确到_____位．
14．绝对值大于1且不大于4的负整数有 __________________．
15．多项式3x2y-7x4y2xy3+27是______次______项式，最高次项的系数是__________.
16．若，则mn的值为 ____.
17．已知代数式的值为8，则代数式_________．
18．写出一个系数是2018，且只含两个字母的四次单项式是_________.
19．若a是不为2的有理数我们把称为a的“哈利数”．如3的“哈利数”是＝﹣2；﹣2的“哈利数”是，已知a1＝3，a2是a1的“哈利数”，a3是a2的“哈利数”，a4是a3的“哈利数”，以此类推，a2019＝___．
20．学习了有理数的加法后，小明同学画出了如图：请问图中①为______，②为______．


三、解答题
21．计算：
22．．
23．计算：．
24．
25．计算
（1）；（2）
26．先化简，再求值：，其中．
27．先化简，后求值：3(a2-ab+7)-2(3ab-a2 +1)+3，其中a=2，b=
28．有理数、、在数轴上的位置如图：

(1)判断正负，用“>”或“<”填空：－c 0，＋ 0，c－ 0.
(2)化简：| b－c|＋|＋b|－|c－a|
29．请观察下列算式，找出规律并填空．
①，②，③，④，……
（1）则第⑩个算式是________．
（2）第n个算式是________．
（3）从以上规律中你可以得到一些启示吗？根据你得到的启示，试解答下题：
若有理数，满足，求的值．
30．对于数轴上的A,B,C三点，给出如下定义：若其中一个点与其它两个点的距离恰好满足2倍的数量关系，则称该点是其它两个点的“联盟点”.
例如数轴上点A,B,C所表示的数分别为1，3，4，此时点B是点A, C的“联盟点”.

（1）若点A表示数-2, 点B表示的数2，下列各数，0，4，6所对应的点分别C1，C2 ，C3 ，C4，其中是点A,B的“联盟点”的是 ；
（2）点A表示数-10, 点B表示的数30，P在为数轴上一个动点：
①若点P在点B的左侧，且点P是点A, B的“联盟点”，求此时点P表示的数；
②若点P在点B的右侧，点P，A, B中，有一个点恰好是其它两个点的“联盟点”，写出此时点P表示的数 .
31．操作题：公元初，中美洲玛雅人使用的一种数字系统与其他计数方式都不相同，它采用二十进位制但只有3个符号，用点“”划“”、卵形“”来表示我们所使用的自然数，如自然数的表示见下表，另外在任何数的下方加一个卵形，就表示把这个数扩大到它的20倍，如表中20和100的表示．

（1）玛雅符号  表示的自然数是______；
（2）请你在右边的方框中画出表示自然数280的玛雅符号：．
32．对于有理数，定义一种新运算“”，规定.
（1）计算的值.
（2）当在数轴上的位置如图所示时，化简.

（3）当时，是否一定有或者？若是，则说明理由；若不是，则举例说明.
（4）已知，求的值.
33．（1）阅读下面材料：

点A、B在数轴上分别表示实数a、b， A、B两点之间的距离表示为AB．
当A、B两点中有一点在原点时，不妨设点A在原点，如图甲，；
当A、B两点都不在原点时：
①如图乙，点A、B都在原点的右边，；
如图丙，点A、B都在原点的左边，；
如图丁，点A、B在原点的两边，．
综上，数轴上A、B两点之间的距离．
（2）回答下列问题：
数轴上表示2和5的两点之间的距离是______，数轴上表示和的两点之间的距离是______，数轴上表示1和的两点之间的距离是______；
数轴上表示x和的两点分别是点A和B，则A、B之间的距离是______，如果，那么______；
当代数式取最小值时，相应的x的取值范围是______．
当代数式取最小值时，相应的x的值是______．
当代数式取最大值时，相应的x的取值范围是______．


参考答案
1．B
【分析】
根据题意，可以知道负数表示向西走，问题得以解决．
【详解】
解：∵向东走9米记作米，
∴米表示向西走5米，
故选：B．
【点睛】
本题考查正数和负数，解答本题的关键是明确正数和负数在题目中的实际意义．
2．C
【分析】
科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．
【详解】
解：380000＝3．8×105．
故选：C．
【点睛】
此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．
3．A
【分析】
根据有理数中整数的定义，有理数的分类，零的意义即可作出选择．
【详解】
解：A. 0的意义是一个也没有，但加上单位后，就不一样了．例如，0℃，它就是温度中的一个值，也是天气中零上和零下的分界点，故本选项错误；
B. 0是偶数不是奇数，故正确；
C. 0不是正数也不是负数，故正确；
D. 0是整数也是有理数，故正确.
故选A.
【点睛】
本题考查了有理数中整数的定义，有理数的分类，零的意义，关键是注意区分，不要混淆．
4．D
【解析】
由数轴上点的位置得：b<0，且|a|<|b|，
∴|a|<−b，a+b<0，ab<0，
故选D.
点睛：本题考查了数轴、绝对值及有理数的加法与乘法，熟练掌握运算法则是解决本题的关键.
5．B
【分析】
先把各数化简，再根据相反数的定义，即可解答．
【详解】
A、−5，−（＋5）＝−5，两数相等，不是相反数；
B、−8，－（−8）＝8，是相反数；
C、＋（−8）＝−8，−（＋8）＝−8，两数相等，不是相反数；
D、8，−（－8）＝8，两数相等，不是相反数；
故选：B．
【点睛】
本题考查了相反数的定义，解决本题的关键是先把各数化简，再根据相反数的定义解答．
6．A
【分析】
根据有理数的加法和乘法法则逐项分析即可．
【详解】
A. 若a0，b0，则a＋b0， ab0，正确；
B. 若a0，b0，则a＋b>0，错误；
C. 若a0，b0，则ab<0，错误；
D. 若 a0，b0，则ab<0，错误；
故选A．
【点睛】
本题考查了有理数的加法和乘法法则，熟练掌握法则中关于符号的确定方法是解答本题的关键．
7．D
【解析】
试题解析：A. 是多项式.错误.
B.的系数为 故错误.
C. ﹣5是单项式,故错误.
D.的次数是3.正确.
故选D.
点睛：数与字母的乘积组成的式子叫做单项式，单独的一个数或字母也是单项式.
8．C
【分析】
根据同类项的定义，所含字母相同且相同字母的指数也相同的项是同类项，可得答案．注意同类项与字母的顺序无关，与系数无关．
【详解】
解：A、都是常数项，所以它们是同类项．故本选项不符合题意;
B. 所含字母相同,相同字母的指数相同，所以它们是同类项．故本选项不符合题意;
C. 相同字母的指数不同,不是同类项，符合题意;
D. 所含字母相同,相同字母的指数相同，所以它们是同类项．故本选项不符合题意;
故选C.
【点睛】
本题考查同类项的定义，同类项定义中的两个“相同”：所含字母相同；相同字母的指数相同，是易混点，还有注意同类项定义中隐含的两个“无关”：①与字母的顺序无关；②与系数无关．
9．A
【分析】
根据绝对值的性质，倒数的定义对各选项分析判断利用排除法求解．
【详解】
A选项，，所以，故A选项正确；
B选项，绝对值小于的整数有1、-1、0，故B选项错误；
C选项，绝对值最小的有理数是0，故C选项错误；
D选项，0没有倒数，故D选项错误；
故选A．
【点睛】
本题考查了绝对值的性质，倒数的定义熟记性质和相关概念是解题的关键．
10．D
【分析】
数轴上单位长度是统一的，利用图象，根据两点之间单位长度是否统一，判断即可．
【详解】
：①当表示天安门东的点所表示的数为0，表示天安门西的点所表示的数为﹣3.5时，表示东单的点所表示的数为6，故①说法正确；
②当表示天安门东的点所表示的数为0，表示天安门西的点所表示的数为﹣7时，表示东单的点所表示的数为12，故②说法正确；
③当表示天安门东的点所表示的数为1，表示天安门西的点所表示的数为﹣2.5时，表示东单的点所表示的数为7，故③说法正确；
④当表示天安门东的点所表示的数为2，表示天安门西的点所表示的数为﹣5时，表示东单的点所表示的数为14，故④说法正确．
故选：D．
【点睛】
本题考查了数轴表示数，数轴的三要素是：原点，正方向和单位长度，因此本题的关键是确定原点的位置和单位长度．
11．, ,
【分析】
根据倒数、相反数和绝对值的定义可直接得出答案.
【详解】
解：∵，
∴﹣1的倒数是，相反数是，绝对值是，
故答案为，，.
【点睛】
本题考查了倒数、相反数和绝对值的定义，熟练掌握基础知识是解题关键.
12．<．
【分析】
由有理数的比较大小的法则进行判断，即可得到答案．
【详解】
解：∵，
∴；
故答案为：<．
【点睛】
本题考查了比较有理数的大小，解题的关键是掌握有理数的比较大小的法则进行解题．
13．百
【解析】
根据近似数的精确度，近似数2.30万精确到百位，
故答案为百
14．−2、−3、−4．
【分析】
首先判断出绝对值大于1且不大于4的负整数的绝对值等于2、3、4，然后判断符合题意负整数有哪些即可．
【详解】
解：∵绝对值大于1且不大于4的负整数的绝对值等于2、3、4，
∴绝对值大于1且不大于4的负整数有−2、−3、−4．
故答案为−2、−3、−4．
【点睛】
此题考查了绝对值的含义和应用，要熟练掌握，解答此题的关键是要明确：①当a是正有理数时，a的绝对值是它本身a；②当a是负有理数时，a的绝对值是它的相反数−a；③当a是零时，a的绝对值是零．
15．6 4 -7
【分析】
分别根据多项式的次数和项数的定义、单项式的系数的定义解答即可.
【详解】
解：多项式3x2y－7x4y2xy3+27是6次4项式，最高次项是－7x4y2，系数是－7.
故答案为：6，4，－7.
【点睛】
本题考查了多项式和单项式的有关概念，属于基础概念题，熟知单项式和多项式的相关概念是关键.
16．9．
【分析】
根据非负数的性质列式求出m、n的值，然后代入代数式进行计算即可得解．
【详解】
由题意得，m+3=0，n-2=0，
解得m=-3，n=2，
所以，mn=（-3）2=9．
故答案为9．
【点睛】
此题考查绝对值和算术平方根非负数的性质，解题关键在于掌握几个非负数的和为0时，这几个非负数都为0．
17．11
【分析】
先求出2x2+3y=1，再把变形后代入，即可求出答案．
【详解】
根据题意得：2x2+3y+7=8，
2x2+3y=1，
所以=3（2x2+3y）+8=3×1+8=11，
故答案为：11．
【点睛】
本题考查了求代数式的值，能够整体代入是解此题的关键．
18．2018ab3（答案不唯一）．
【分析】
把2018看作单项式的系数，再写出a、b的指数和为4的单项式即可．
【详解】
∵单项式的系数为2018，次数为4，
∴符合条件的单项式可以为：2018ab3（答案不唯一）．
故答案为：2018ab3（答案不唯一）．
【点睛】
本题考查的是单项式，熟知单项式系数及次数的定义是解答此题的关键．
19．.
【分析】
分别求出数列的前5个数得出该数列每4个数为一周期循环，据此可得答案
【详解】
∵a1＝3，
∴a2＝＝﹣2，
a3＝，
a4＝＝，
a5＝＝3，
∴该数列每4个数为1周期循环，
∵2019÷4＝504…3，
∴，a2019＝a3＝．
故答案为: .
【点睛】
本题考查了数字的规律变化，通过观察数字，分析、归纳并发现其中的规律，并应用规律解决问题是解题的关键．
20．取相同符号 用较大绝对值减去较小绝对值
【分析】
根据有理数的加法法则即可得出结论．
【详解】
解：由程序图可知：①是关于同号相加时的符号问题：取相同符号
②是关于异号相加时，计算问题：用较大绝对值减去较小绝对值
故答案为：取相同符号；用较大绝对值减去较小绝对值．
【点睛】
此题考查的是有理数的加法，掌握有理数的加法法则是解决此题的关键．
21．
【分析】
先把减法转化为加法，再利用有理数的加法法则进行运算即可得到答案．
【详解】
解：



【点睛】
本题考查的是有理数的加减混合运算，掌握把减法转化为加法运算是解题的关键．
22．-5
【分析】
根据乘法的分配律进行计算即可．
【详解】



．
【点睛】
本题主要考查了有理数的混合运算，解题的关键是运用乘法分配律计算．
23．
【分析】
先算乘方，再算乘法，最后算加减．
【详解】
解：原式＝
＝
＝．
【点睛】
本题考查有理数的混合运算法则，难度较小．
24．-23
【分析】
根据实数的运算顺序，先算乘方，再算乘除，最后算加减即得．
【详解】
解：原式=
=
=-23．
【点睛】
本题考查有理数的混合运算，按照实数运算顺序计算是解题关键，按照乘法与除法运算法则确定符号是易错点．
25．（1）；（2）
【分析】
（1）先去括号，再合并同类项即可；（2）先去小括号，再去中括号，最后合并同类项即可；
【详解】
解：
（1）原式=8a-8b-5a+5b-7a+7b
=-4a+4b
(2) 原式=
=
=
【点睛】
本题主要考查了整式的加减，掌握整式的加减运算法则，合并同类项是解题的关键.
26．0
【解析】
原式=6m2-4m-6m2+2-10=-4m-8.
当m=-2时，
原式=-4m-8=-4×(-2)-8=8-8=0.
27．5a2－9ab +22，36.
【分析】
先去括号，再合并同类项，然后把a、b的值代入化简后的式子中计算即可.
【详解】
解：
=
=
当a=2，b=时，
原式=.
【点睛】
本题考查的是整式的加减运算与化简求值，属于常考题型，熟练掌握整式的加减运算法则是解题关键.
28．（1）<,<, >;（2）-2b
【分析】
（1）根据数轴得出a<0 （2）去掉绝对值符号，合并同类项即可．
【详解】
(1)∵从数轴可知：a<0 ∴b−c<0，a+b<0，c−a>0，
(2)∵b−c<0，a+b<0，c−a>0，
∴|b−c|+|a+b|−|c−a|=c−b+(−a−b)−(c−a)=c−b−a−b−c+a=−2b.
【点睛】
此题考查数轴、绝对值、整式的加减，解题关键在于结合数轴判断绝对值的大小.
29．（1）；（2）；（3）
【分析】
（1）根据所给的算式，可找出规律：，再分析即可；
（2）根据（1）中的规律即可得出
（3）利用绝对值的非负性求得a、b，再根据得到的规律进行运算求值．
【详解】
解：（1）
（2）
（3）由题意知：，
原式





【点睛】
本题主要是寻找规律，再根据有理数的混合运算计算，并利用了两个非负数的和等于0，则每一个非负数等于0的知识．
30．（1），；（2）①－50或或；②50或70或110.
【分析】
（1）题目给定的规律，联盟点必须满足其中一个点与其它两个点的距离恰好满足2倍的数量关系，根据规律找出即可（2）已知点A的大小，点B的大小，根据不同的位置分别找出点P的坐标即可.
【详解】
解：（1），；
（2）① 设点P表示的数为x，

如图，当点在点A左侧时，，
则 30－x＝2（－10－x），
解得 x＝－50.
所以点表示的数为－50；
如图，当点在线段AB上且时，

则 30－x＝2（x＋10），
解得 x＝.
所以点表示的数为；
如图，当点在线段AB上且时，

则 x＋10＝2（30－x），
解得 x＝.
所以点表示的数为.
综上所述，当点P在点B的左侧时，点P表示的数为－50或或.
② 50或70或110.
【点睛】
此题重点考察学生对坐标轴上的点的大小的理解，理解数轴上的点的大小是解题的关键.
31．；．
【分析】
（1）由图分析可知，一横代表一个5，一个点代表一个1，即可得出结论;
（2）根据280=（4＋5×2）×20，结合题意即可画出图形．
【详解】
解：玛雅符号表示的自然数是3＋5×3=18
 故答案为：；
∵280=（4＋5×2）×20
∴表示自然数的玛雅符合为：．
故答案为：．
【点睛】
本题考查类比推理，务必充分利用题干所给信息，进行合理的类比推理是解题关键．
32．（1）6；（2）-2b；（3）不一定，理由见解析；（4）或-．
【分析】
（1）原式利用题中的新定义计算即可得到结果；
（2）根据数轴上点的位置判断出a+b与a-b的正负，利用绝对值的代数意义计算即可得到结果；
（3）当a⊙b=a⊙c时，不一定有b=c或者b=-c，举例即可；
（4）分类讨论a的正负，利用新定义将已知等式化简，即可求出a的值．
【详解】
（1）根据题中的新定义得：2⊙（-3）=|2+（-3）|+|2-（-3）|=1+5=6；
（2）从a，b在数轴上的位置可得a+b＜0，a-b＞0，
∴a⊙b=|a+b|+|a-b|=-（a+b）+（a-b）=-2b；
（3）由a⊙b=a⊙c得：|a+b|+|a-b|=|a+c|+|a-c|，
不一定有b=c或者b=-c，
例如：取a=5，b=4，c=3，则|a+b|+|a-b|=|a+c|+|a-c|=10，
此时等式成立，但b≠c且b≠-c；
（4）当a≥0时，（a⊙a）⊙a=2a⊙a=4a=8+a，
解得：a=；
当a＜0时，（a⊙a）⊙a=（-2a）⊙a=-4a=8+a，
解得：a=-．
故a的值为：或-．
【点睛】
此题考查了有理数的混合运算，熟练掌握运算法则是解本题的关键．
33．①3，3，4；②，1或3；③；④；⑤
【分析】
①根据中的知识可以得到两点之间的距离就是较大的数与较小的数的差，据此即可求解；
②根据，即可直接写出结果；
③表示数轴上一点到与5两点的距离的和，当这点是或5，以及它们之间时和最小，最小距离是与5之间的距离；
④代数式表示数轴上一点到1、与5三点的距离的和，根据两点之间线段最短，则当时和最小，最小值是5到的距离；
⑤代数式表示数轴上一点到5与两点的距离的差，当点小于等于时差最大，最大值是5与之间的距离．
【详解】
解：①，，；
故答案为：3；3；4；
②数轴上表示x和的两点分别是点A和B，则A、B之间的距离是，
当AB=2时，则
则或
故答案为：；1或3；
③表示数轴上一点到与5两点的距离的和，当这点在和5之间时和最小，最小距离是：
故答案为：；
④代数式表示数轴上一点到1、与5三点的距离的和，根据两点之间线段最短，则当时和最小，最小值是5到的距离，是
故答案为：；
⑤代数式表示数轴上一点到5与两点的距离的差，当点所表示的数小于等于时差最大，最大值是5与之间的距离，是7．
故答案是：．
【点睛】
此题考查的是数轴与绝对值的关系，掌握两点之间的距离公式是解决此题的关键．