【名校Word】重庆市西南大学附中高2018届高三第四次月考理数试题

这是一份【名校Word】重庆市西南大学附中高2018届高三第四次月考理数试题，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
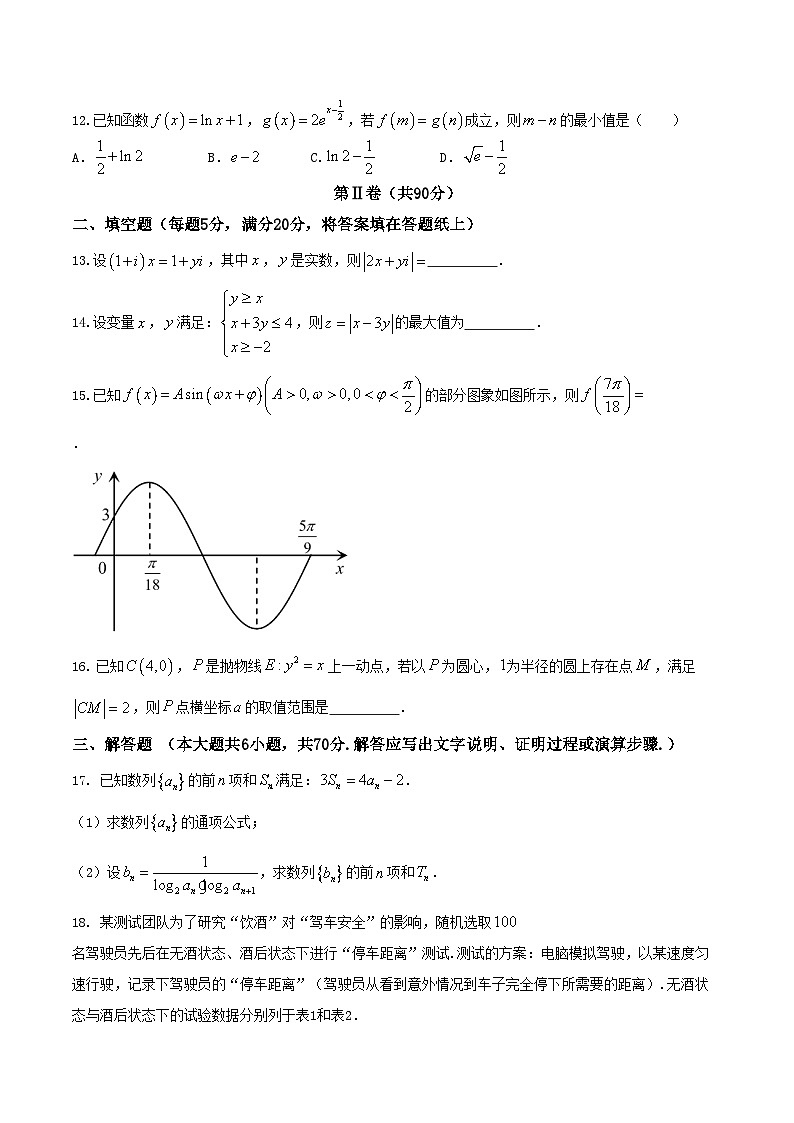
西南大学附属中学校高2018级第四次月考数学试题（理）第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.设集合，，则（    ）A．         B．       C．       D．2.下列说法正确的是（    ）A．“”是“函数是奇函数”的充要条件         B．样本的相关系数，越接近于，线性相关程度越小       C．若为假命题，则，均为假命题       D．“若，则”的否命题是“若，则”3.等比数列中，，，则（    ）A．         B．       C．        D． 4.已知，，，则（    ）A．         B．       C.         D．5.已知定义在上的函数，记，，，则、、的大小关系是（    ）A．         B．       C.         D．6.某程序框图如图所示，该程序运行后输出的值是，则（    ）A．         B．       C.         D．7.设曲线及直线所围成的封闭图形为区域，不等式组所确定的区域为，在区域内随机取一点，则该点恰好在区域内的概率为（    ）A．         B．       C.         D．8.已知，的最大值为，则（    ）A．         B．       C.         D．9.某个班级组织元旦晚会，一共准备了、、、、、六个节目，节目演出顺序第一个节目只能排或，最后一个节目不能排，且、要求相邻出场，则不同的节目顺序共有（    ）种A．         B．       C.         D．10.若函数有一个极值点为，且，则关于的方程的不同实数根个数不可能为（    ）A．         B．       C.         D．11.已知双曲线的左、右顶点分别为、，是上一点，为等腰三角形，且外接圆面积为，则双曲线的离心率为（    ）A．         B．       C.         D．12.已知函数，，若成立，则的最小值是（    ）A．         B．       C.         D．第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13.设，其中，是实数，则          ．14.设变量，满足：，则的最大值为          ．15.已知的部分图象如图所示，则          ．16. 已知，是抛物线上一动点，若以为圆心，为半径的圆上存在点，满足，则点横坐标的取值范围是          ．三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） 17. 已知数列的前项和满足：.（1）求数列的通项公式；（2）设，求数列的前项和.18. 某测试团队为了研究“饮酒”对“驾车安全”的影响，随机选取名驾驶员先后在无酒状态、酒后状态下进行“停车距离”测试.测试的方案：电脑模拟驾驶，以某速度匀速行驶，记录下驾驶员的“停车距离”（驾驶员从看到意外情况到车子完全停下所需要的距离）.无酒状态与酒后状态下的试验数据分别列于表1和表2．表1停车距离（米）频数24422491表2平均每毫升血液酒精含量毫克1030507090平均停车距离米3050607090回答以下问题．（1）由表1估计驾驶员无酒状态下停车距离的平均数；（2）根据最小二乘法，由表2的数据计算关于的回归方程；（3）该测试团队认为：驾驶员酒后驾车的平均“停车距离”大于（1）中无酒状态下的停车距离平均数的倍，则认定驾驶员是“醉驾”.请根据（2）中的回归方程，预测当每毫升血液酒精含量大于多少毫克时为“醉驾”？（精确到个位）（附：对于一组数据，，…，，其回归直线的斜率和截距的最小二乘估计分别为，）19. 已知函数.（1）求的对称轴所在直线方程及其对称中心；（2）在中，内角、、所对的边分别是、、，且，，求周长的取值范围．20. 已知椭圆的两个焦点与短轴的一个顶点构成底边为，顶角为的等腰三角形．（1）求椭圆的方程；（2）设、、是椭圆上三动点，且，线段的中点为，，求的取值范围．21. 函数，.（1）求函数的单调区间及极值；（2）若，是函数的两个不同零点，求证：①；②.请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.22.选修4-4：坐标系与参数方程已知平面直角坐标系中，过点的直线的参数方程为（为参数），与轴交于，以该直角坐标系的原点为极点，轴的非负半轴为极轴建立极坐标系．曲线的极坐标方程为，直线与曲线交于、两点．（1）求曲线的直角坐标方程和点的一个极坐标；（2）若，求实数的值．23.选修4-5：不等式选讲已知函数.（1）对，都有恒成立，求的取值范围；（2）设不等式的解集为，若，求证：.       试卷答案一、选择题1-5:BDACD       6-10:BCCBA      11、12：CA二、填空题13.          14.           15.           16.三、解答题17.解：（1）∵ ①当时，，∴当时， ②由①-②得：∴∴是以为首项，公比为的等比数列∴（2）∵∴18.解：（1）（2）   ∴∴回归方程为（3）由题意知：，∴∴预测当每毫升血液酒精含量大于毫克时为“醉驾”19.解：（1）由，∴∴的对称轴方程为，由，∴，∴的对称中心为，（2）法一：∵，∴，∵，∴∴，∴由正弦定理得：∴，∴∵，∴∴的周长范围为法二：∵，∴，∴，∴，得：，，∴又，∴，∴20.解：（1）由题意，，，∴，∴椭圆（2）设，，，由∴，得：法一：当的斜率不存在时，，由,，得，∴，当的斜率存在时，设得：，，得：，此时总成立又，∴，∴且，∴且综上：法二：设中点，则，∴∴设，则∴21.解：（1）定义域：  令，则，令，则∴在递减，递增∴，无极大值（2）由（1）知时，；时，要使有两个不同零点，则即不妨设，①证明：令，则在递增而，∴∴即∵，∴∵且在递减∴，即②证明：令，下面先证明，∵，，∴在递增∴，∴在递增，∴即在总成立，∵，∴又∵由知，又，且及在递减∴，即22.解：（1），（2）将代入得∵，∴∴，∴23.解：（1）∵，∴∴在上递减，在上递增，当时为常数∴，∴（2）∵，∴∵∵,∴,,∴,∴，∴，∴