



四川省高考数学复习 专题08 统计与概率(文科)解答题30题专项提分计划
展开四川省高考数学复习
专题8统计与概率(文科)解答题30题专项提分计划
1.(2023·四川南充·四川省南充高级中学校考模拟预测)某电子产品生产商经理从众多平板电脑中随机抽取6台,检测它们充满电后的工作时长(单位:分钟), 相关数据如下表所示.
平板电脑序号
1
2
3
4
5
6
工作时长/分
220
180
210
220
200
230
(1)若从被抽中的6台平板电脑中随机抽出2台,则抽出的2台平板电脑充满电后工作时长都不小于210分钟的概率;
(2)下表是一台平板电脑的使用次数与当次充满电后工作时长的相关数据.求该平板电脑工作时长与使用次数之间的回归直线方程,并估计该平板电脑使用第200次时充满电后的工作时长.
使用次数x/次
20
40
60
80
100
120
140
工作时长/分
210
206
202
196
191
188
186
附: ,,.
【答案】(1)
(2);分钟.
【分析】(1)使用古典概型概率公式进行求解即可;
(2)使用表格中的数据,根据题目所附公式进行计算,并将代入回归直线方程进行估计即可.
【详解】(1)用表示从被抽中的6台平板电脑中随机抽出2台的序号分别为和,
则基本事件有,,,,,,,,,,,,,,共个,
将“抽出的2台平板电脑充满电后工作时长都不小于210分钟”记为事件,
由已知,序号为,,,的平板电脑充满电后工作时长都不小于210分钟,
∴事件中基本事件有,,,,,共个,
∴.
∴若从被抽中的6台平板电脑中随机抽出2台,则抽出的2台平板电脑充满电后工作时长都不小于210分钟的概率为.
(2)由已知,,
,
,
,
∴,
∴,
∴线性回归直线方程为,
当时,,
∴估计该平板电脑使用第200次时充满电后的工作时长为分钟.
2.(四川省凉山州2023届高三第一次诊断性检测数学(文)试题)2022年卡塔尔世界杯(英语:FIFA World Gup Qatar 2022)是第二十二届世界杯足球赛,是历史上首次在卡塔尔和中东国家境内举行,也是继2002年韩日世界杯之后时隔二十年第二次在亚洲举行的世界杯足球赛,除此之外,卡塔尔世界杯还是首次在北半球冬季举行,第二次世界大战后首次由从未进过世界杯的国家举办的世界杯足球赛.为了解某校学生对足球运动的兴趣,随机从该校学生中抽取了100人进行调查,其中女生中对足球运动没兴趣的占女生人数的,男生有5人表示对足球运动没有兴趣.
(1)完成列联表,并回答能否有的把握认为“该校学生对足球是否有兴趣与性别有关”?
有兴趣
没兴趣
合计
男
60
女
合计
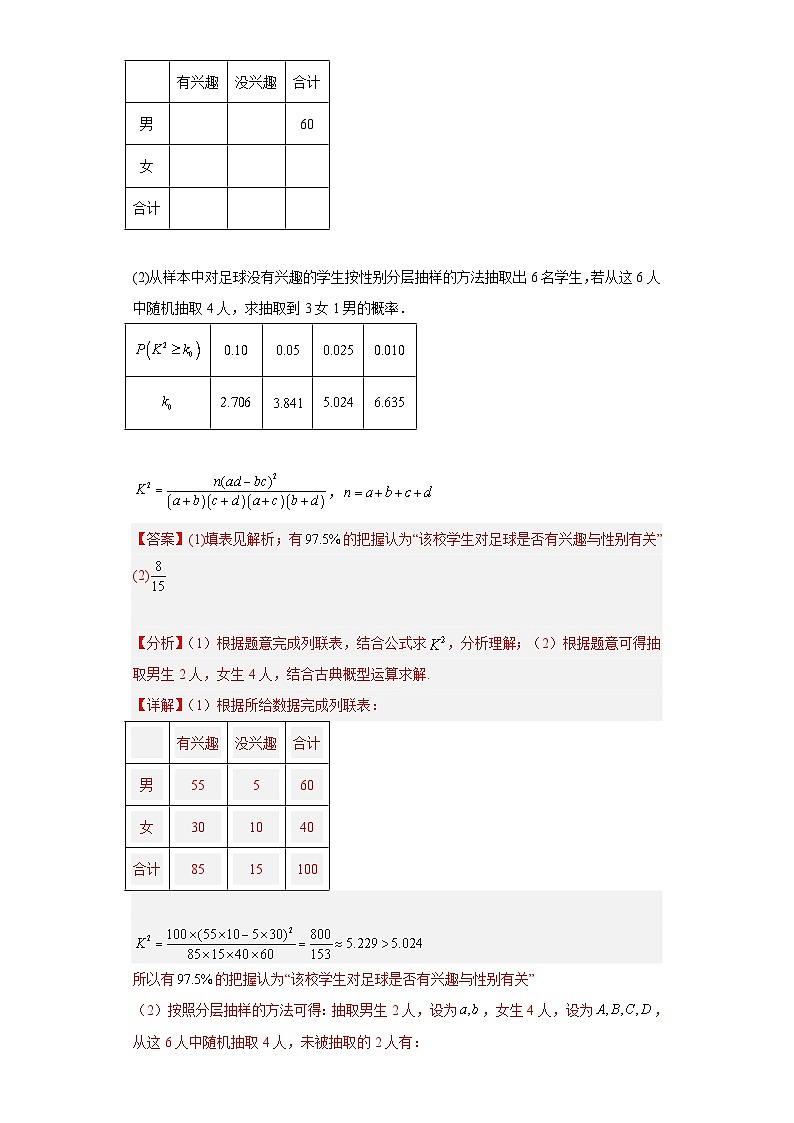
(2)从样本中对足球没有兴趣的学生按性别分层抽样的方法抽取出6名学生,若从这6人中随机抽取4人,求抽取到3女1男的概率.
,
【答案】(1)填表见解析;有的把握认为“该校学生对足球是否有兴趣与性别有关”
(2)
【分析】(1)根据题意完成列联表,结合公式求,分析理解;(2)根据题意可得抽取男生2人,女生4人,结合古典概型运算求解.
【详解】(1)根据所给数据完成列联表:
有兴趣
没兴趣
合计
男
55
5
60
女
30
10
40
合计
85
15
100
所以有的把握认为“该校学生对足球是否有兴趣与性别有关”
(2)按照分层抽样的方法可得:抽取男生2人,设为,女生4人,设为,
从这6人中随机抽取4人,未被抽取的2人有:
,
共有15种不同的基本结果.
其中抽取到3女1男的情况,即未被抽取的2人是1男1女,则有:,共有8种不同的基本结果,
所以抽取到3女1男的概率为.
3.(四川省营山县第二中学2023届高三第六次高考模拟检测数学(文科)试题)为了丰富大学生的课外生活,某高校团委组织了有奖猜谜知识竞赛,共有名学生参加,随机抽取了名学生,记录他们的分数,将其整理后分成组,各组区间为,,,,并画出如图所示的频率分布直方图
(1)估计所有参赛学生的平均成绩各组的数据以该组区间的中间值作代表;
(2)若团委决定对所有参赛学生中成绩排在前名的学生进行表彰,估计获得表彰的学生的最低分数线
【答案】(1)分
(2)分
【分析】(1)利用频率分布直方图频率和为1计算再计算平均数;
(2) 获得表彰的学生人数的频率为,进而可得最低分数线在内,再进行求解.
【详解】(1)由,得
这名参赛学生的平均成绩约为分,
故估计所有参赛学生的平均成绩为分
(2)获得表彰的学生人数的频率为,
设获得表彰的学生的最低分数线为,由分数在区间的频率为,可知,
由,得,
故估计获得表彰的学生的最低分数线为分
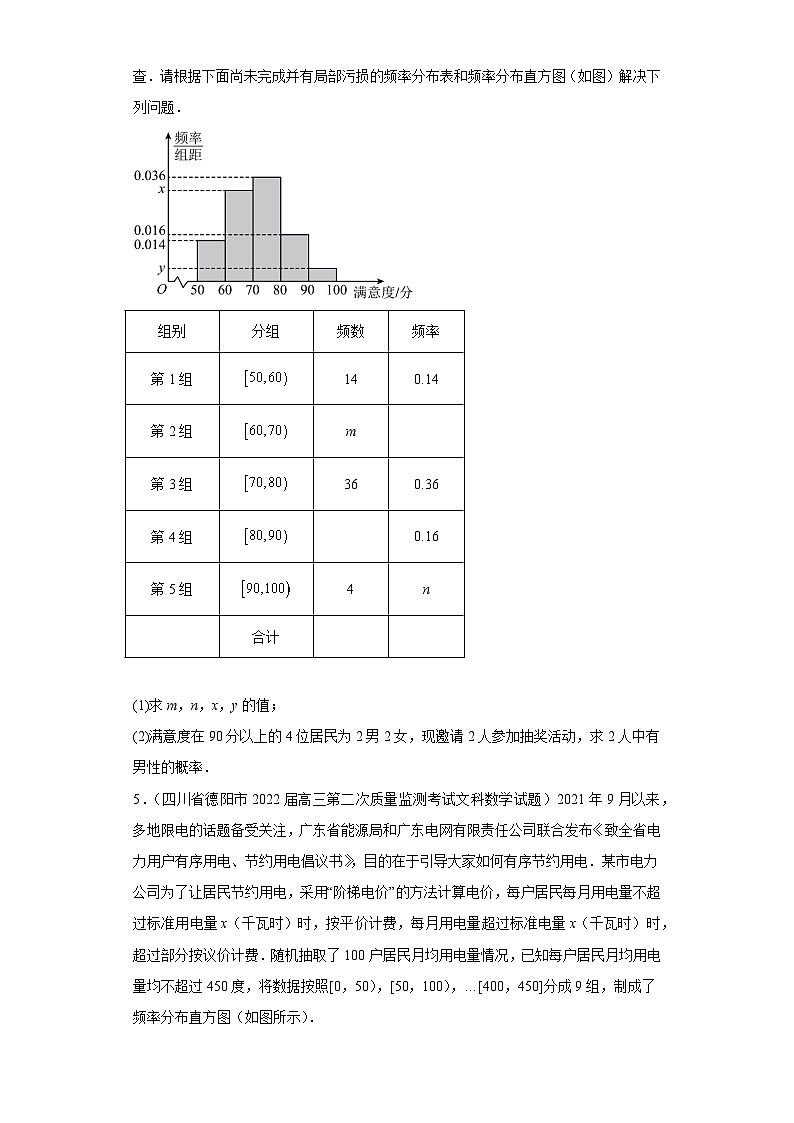
4.(四川省成都市第七中学2022-2023学年高三下学期入学考试数学(文)试题)随着人民生活水平的不断提高,“衣食住行”愈发被人们所重视,其中对饮食的要求也愈来愈高.某地区为了解当地餐饮情况,随机抽取了100人对该地区的餐饮情况进行了问卷调查.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图)解决下列问题.
组别
分组
频数
频率
第1组
14
0.14
第2组
m
第3组
36
0.36
第4组
0.16
第5组
4
n
合计
(1)求m,n,x,y的值;
(2)满意度在90分以上的4位居民为2男2女,现邀请2人参加抽奖活动,求2人中有男性的概率.
【答案】(1),,,
(2)
【分析】(1)直接根据频率分布表和频率分布直方图计算即可;
(2)利用列举法结合古典概型求解即可.
【详解】(1)由题意可得第四组的人数为,
所以,,
又内的频率为,所以,
内的频率为0.04,所以;
(2)设四个人为男1、男2、女1、女2,
抽两人有男1男2、男1女1、男1女2、男2女1、男2女2、女1女2,共6种情况,
有男性的情况是男1男2、男1女1、男1女2、男2女1、男2女2,总共5种,
所以2人中有男性的概率为.
5.(四川省德阳市2022届高三第二次质量监测考试文科数学试题)2021年9月以来,多地限电的话题备受关注,广东省能源局和广东电网有限责任公司联合发布《致全省电力用户有序用电、节约用电倡议书》,目的在于引导大家如何有序节约用电.某市电力公司为了让居民节约用电,采用“阶梯电价”的方法计算电价,每户居民每月用电量不超过标准用电量x(千瓦时)时,按平价计费,每月用电量超过标准电量x(千瓦时)时,超过部分按议价计费.随机抽取了100户居民月均用电量情况,已知每户居民月均用电量均不超过450度,将数据按照[0,50),[50,100),…[400,450]分成9组,制成了频率分布直方图(如图所示).
(1)求直方图中m的值;
(2)如果该市电力公司希望使85%的居民每月均能享受平价电费,请估计每月的用电量标准x(千瓦时)的值;
(3)在用电量不小于350(千瓦时)的居民样本中随机抽取2户,求其中不小于400(千瓦时)的恰好有1户居民的概率.
【答案】(1)
(2)
(3)
【分析】(1)由频率分布直方图的性质列出方程,能求出.
(2)由频率分布直方图求出的频率为0.73,的频率为0.15,该市电力公司希望使的居民每月均能享受平价电费,由此能估计每月的用电量标准的值.
(3)根据频率分布直方图求出用电量不小于350(千瓦时)的居民户数,与不小于400(千瓦时)的居民户数,再用列举方程列出所有可能结果,最后根据古典概型的概率公式计算可得;
(1)
解:由频率分布直方图得:
.
解得.
(2)
解:的频率为,
的频率为,
该市电力公司希望使的居民每月均能享受平价电费,
估计每月的用电量标准.
(3)
解:用电量不小于350(千瓦时)的居民样本有:户,其中不小于400(千瓦时)的有户,记的4户为、、、,的2户为、,从6户中随机抽取户可能结果有、、、、、、、、、、、、、、共15个;其中不小于400(千瓦时)的恰好有1户居民的有、、、、、、、共8个,故其中不小于400(千瓦时)的恰好有1户居民的概率;
6.(四川省凉山州2022届高三第二次诊断性检测数学(文科)试题)四川省凉山州各种特产、小吃尤其丰富,凉山州会理市羊肉粉早在清代中叶就名扬遐迩.凡来会理市品尝过会理市羊肉粉的人,无不交口称赞.尤其在冬季,吃一碗滚烫的羊肉粉,浑身暖和.羊肉粉的主要原料是羊肉和米粉制作有特殊的讲究,要选择山坡放养,体重在八九十斤左右的黑山羊宰杀,将羊头、羊腿、羊蹄、羊油、羊下水全部放进能装一、两百斤的大铁锅,掺上几里路运来优质山泉水,加上老姜、花椒、胡椒、白扣,等佐料,先要猛火烧开,用漏瓢捞出汤上面的泡沫,再用中火慢慢炖,时间达六、七个小时熬制呈乳白色米汤-样的原汤;羊肉粉的米线,是用会理农村本地产的稻谷跟大米制作出来,韧性好,饭粒不生硬,入口柔和,口味有大米的天然芳香;米粉要经过特殊处理:将水烧开,放入米粉,烧开捞起,放入冷水里(不停换水,直至冷却).会理市某羊肉粉店每天早晨处理好当天的米粉,以12元碗的价格售出,每碗获利5元,当天卖不出的米粉则每碗亏损2元,该店记录了30天的日需求量(单位:碗),整理如下表:
日需求量
80
90
100
110
频数
5
10
7
8
(1)以样本估计总体,求该店采粉日需求量的平均数;
(2)以30天记录的日需求量的频率为概率,该店每天准备100碗米粉,记该店每天获得的利润为Y(单位:元),写出Y的所有可能值,并估计Y低于450元的概率.
【答案】(1)96;
(2)可能取值为360,430,500,.
【分析】(1)利用求平均数的公式即得;
(2)分别求得日需求量碗,碗和100碗以上时的日利润和对应概率,即得.
【详解】(1)该米粉店日需求量的平均数为:;
(2)当日需求量为80碗时,该店每天获利
当日需求量为90碗时,该店每天获利(元);
当日需求量为100碗以上时,该店每天获利(元).
所以,Y的可能取值为360,430,500
所以,Y低于450元的概率为.
7.(四川省攀枝花市2022届高三第二次统一考试文科数学试题)某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别,,,,(单位:克)中,经统计频率分布直方图如图所示.
(1)估计这组数据的平均数;
(2)在样本中,按分层抽样从质量在,中的芒果中随机抽取5个,再从这5个中随机抽取2个,求这2个芒果都来自同一个质量区间的概率;
(3)某经销商来收购芒果,同一组中的数据以这组数据所在区间中点的值作代表,用样本估计总体,该种植园中共有芒果大约10000个,经销商提出以下两种收购方案:方案①:所有芒果以10元/千克收购;方案②:对质量低于350克的芒果以3元/个收购,对质量高于或等于350克的芒果以5元/个收购.请通过计算确定种植园选择哪种方案获利更多?
【答案】(1);
(2);
(3)选择方案②获利多.
【分析】(1)根据区间的频率和区间中点的坐标进行求解即可;
(2)根据分层抽样的性质,用列举法,结合古典概型的计算公式进行求解即可;
(3)根据两个不同方案进行计算求解判断即可.
【详解】(1)由频率分布直方图知,各区间频率为,
这组数据的平均数为:;
(2)利用分层抽样从这两个范围内抽取5个芒果,则质量在内的芒果有2个,记为,,质量在内的芒果有3个,记为;
从抽取的5个芒果中抽取2个共有10种不同情况:,
记事件为“这2个芒果都来自同一个质量区间”,则有4种不同组合:
从而,故这2个芒果都来自同一个质量区间的概率为;
(3)方案①收入:(元);
方案②:低于350克的芒果收入为(元;
不低于350克的支果收入为(元);
故方案②的收入为(元).
由于,所以选择方案(2)获利多.
8.(四川省攀枝花市2022届高三第三次统一考试文科数学试题)2022年2月4日,北京冬奥会盛大开幕,这是让全国人民普遍关注的体育盛事,因此每天有很多民众通过手机、电视等方式观看相关比赛.某机构将每天收看相关比赛的时间在2小时以上的人称为“冰雪运动爱好者”,否则称为“非冰雪运动爱好者”,该机构通过调查,并从参与调查的人群中随机抽取了100人进行分析,得到下表(单位:人):
冰雪运动爱好者
非冰雪运动爱好者
合计
女性
20
50
男性
15
合计
100
(1)将上表中的数据填写完整,并判断能否在犯错误的概率不超过0.005的前提下认为性别与是否为“冰雪运动爱好者”有关?
(2)现从抽取的女性人群中,按“冰雪运动爱好者”和“非冰雪运动爱好者”这两种类型进行分层抽样抽取5人,然后再从这5人中随机选出3人,求其中至少有1人是“冰雪运动爱好者”的概率.
附:,其中.
0.05
0.025
0.010
0.005
0.001
3.841
5.024
6.635
7.879
10.828
【答案】(1)表格见解析,能.
(2).
【分析】(1)补全列联表,根据公式计算,与表中数据比较即可判断;
(2)按分层抽样,5人中有2人是“冰雪运动爱好者”,编号为a、b,3人为“非冰雪运动爱好者”,编号为1、2,列举出从这5人中随机选出3人共有10种不同情况和其中没有人是“冰雪运动爱好者”的情况,根据古典概型概率计算即可.
(1)
列联表如下:
冰雪运动爱好者
非冰雪运动爱好者
合计
女性
20
30
50
男性
35
15
50
合计
55
45
100
,
能在犯错误的概率不超过的前提下认为“冰雪运动爱好者”或“非冰雪运动爱好者”与性别有关;
(2)
从抽取的女性人群中,按“冰雪运动爱好者”和“非冰雪运动爱好者”这两种类型进行分层抽样抽取5人,
则5人中“冰雪运动爱好者”为人,记为a、b;
“非冰雪运动爱好者”为人,记为1、2、3.
再从这5人中随机选出3人共有10种不同情况:.
记事件为其中没有人是“冰雪运动爱好者”,则有1种:﹒
从而其中至少有1人是“冰雪运动爱好者”的概率为1-.
9.(四川省内江市2022届高三第三次模拟考试数学(文)试题)2021年某省约有23万文科考生参加高考,除去成绩在600分及以上的2013人与成绩在400分以下的109600人,还有约11.87万文科考生的成绩集中在区间内,其成绩的频率分布如下表所示:
分数段
频率
0.21
0.26
0.27
0.18
0.08
(1)请估计该次高考文科考生成绩在内的平均数(同一组中的数据用该组区间的中点值代表);
(2)若在分数段和的考生中采用分层抽样的方法抽取5名考生进行电话访问,再从被电话访问的5名考生中随机抽取3名考生进行问卷调查,求进行问卷调查的3名考生中至少有2名分数低于520分的概率
【答案】(1);
(2).
【分析】(1)根据频率直方表求平均数即可.
(2)由分层抽样的性质确定、中所抽取的考生人数,再应用列举法求随机抽取3名考生的组合情况,并确定至少有2名分数低于520分即可求概率.
(1)
该次高考文科考生成绩在内的平均分的估计值为.
(2)
分数段和的考生人数的比为,
在分数段的考生中应抽取名,记,,.
在分数段的考生中应抽取名,记,.
从上述5名考生中随机抽取3名的所有结果为,,,,,,,,,共10种,
其中至少有2名分数低于520分的结果为,,,,,,共7种.
所以进行问卷调查的3名考生中至少有2名分数低于520分的概率.
10.(四川省泸县第二中学2022届高考仿真考试(一)文科数学试题)共享单车进驻城市,绿色出行引领时尚.某市有统计数据显示,某站点6天的使用单车用户的数据如下,用两种模型①;②分别进行拟合,得到相应的回归方程,进行残差分析得到如表所示的残差值及一些统计量的值:(残差=真实值-预测值)
日期x(天)
1
2
3
4
5
6
用户y(人)
13
22
43
45
55
68
模型①的残差值
-1.1
-2.8
m
-1.2
-1.9
0.4
模型②的残差值
0.3
-5.4
4.3
n
-1.6
3.8
(1)(ⅰ)求表格中m,n的值;
(ⅱ)残差值的绝对值之和越小说明模型拟合效果越好.根据表中数据,比较模型①,②的拟合效果,应选择哪一个模型?并说明理由;
(2)残差绝对值大于3的数据认为是异常数据,需要剔除,剔除异常数据后,重新求出(1)中所选模型的回归方程.
(参考公式:)
【答案】(1)(ⅰ);(ⅱ)应该选模型①,理由见解析;
(2).
【分析】(1)(ⅰ)根据已知数据和对应模型求出对应残差,即可得m,n;(ⅱ)比较两个模型所得残差的绝对值之和的大小,即可确定模型的拟合效果,进而选择模型.
(2)根据题意去除异常数据,再应用最小二乘法求回归直线方程.
(1)
(ⅰ),故;
,故.
(ⅱ)应该选择模型①,理由如下:
模型①的残差值的绝对值之和为,
模型②的残差值的绝对值之和为.
由14.9<18.6,则模型①的拟合效果较好,应该选模型①.
(2)
剔除异常数据,即剔除第3天的数据后,得,,
∴,.
∴y关于x的回归方程为.
11.(四川省雅安市2022届高三第三次诊断性考试数学(文)试题)如今快寄成为不少人日常生活中不可或缺的一部分.某市一调查机构针对该市市场占有率最高的甲、乙两家快寄企业(以下简称快寄甲、快寄乙)的经营情况进行了调查,调查结果如下表:
日期
1
2
3
4
5
快寄甲日接单量x/百单
5
2
9
8
11
快寄乙日接单量y/百单
2.2
2.3
10
5
15
据统计表明y与x之间具有线性相关关系,并经计算求得y与x之间的回归方程为.
(1)求;
(2)假定快寄企业平均每单能获纯利润3元,试预测当快寄乙日接单量不低于2500单时,快寄甲日接单量的最小值(结果精确到单)及所获取的日纯利润的最小值.
【答案】(1)
(2)快寄乙日接单量最小值为2010单,快寄乙日纯利润最小值为元
【分析】(1)求出样本中心点,再根据线性回归方程必过样本中心点即可得解;
(2)由(1)结合题意列出不等式,求出的最小值,从而可得出答案.
(1)
解:,,
所以;
(2)
解:由题意y与x之间的回归方程为,
由,解得,
所以快寄乙日接单量最小值为2010单,
所以快寄乙日纯利润最小值为元.
12.(四川省成都市温江区2022届高考适应性考试数学(文)试题)北京某大学为了了解大一新生喜欢打篮球是否与性别有关,对学校一百名新生进行了初步统计,得到如下列联表:
喜欢打篮球
不喜欢打篮球
合计
男
40
女
50
合计
在这100名新生中每5个人就有3个人喜欢打篮球.
(1)把上述列联表补充完整;
(2)请问,是否有99.9%的把握认为喜欢打篮球与性别有关?说明你的理由;
(3)被调查的学生中基础数学专业有5名学生,其中3名喜欢打篮球,现从这5名学生中随机抽取2人,求恰有1人喜欢打篮球的概率.
附表:
P(K2≥k)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828
参考公式:的观测值:(其中)
【答案】(1)填表见解析
(2)有99.9%的把握认为喜欢打篮球与性别有关;理由见解析
(3)
【分析】(1)由题意可计算喜欢打篮球的人数为60,根据表格内容即可补充列联表.(2)计算的观测值可得出结论.(3)5名学生中喜欢打篮球的3名学生记为a,b,c,另外2名学生记为甲,乙,列举法可计算概率值.
(1)
因为在这100名新生每5个人中就有3个人喜欢打篮球,
所以喜欢打篮球的学生人数为人
其中男生有40人,则女生有20人,列联表补充如下:
喜欢打篮球
不喜欢打篮球
合计
男生。
40
10
50
女生
20
30
50
合计
60
40
100
(2)
因为,
所以有99.9%的把握认为喜欢打篮球与性别有关.
(3)
5名学生中喜欢打篮球的3名学生记为a,b,c,另外2名学生记为甲,乙,任取2名学生,则所有可能情况为(a,b)、(a,c)、(a,甲)、(a,乙)、(b,c)、(b,甲)、(b,乙)、(c,甲)、(c,乙)、(甲,乙),共10种.
其中恰有1人喜欢打篮球的可能情况为(a,甲)、(a,乙)、(b,甲)、(b,乙)、(c,甲)、(c,乙),共6种.
所以恰好有1人喜欢打篮球的概率为.
13.(四川省内江市高中2023届零模考试数学文科试题)年北京冬奥会即第届冬季奥林匹克运动会在年月日至月日在北京和张家口举行.某研究机构为了解大学生对冰壶运动是否有兴趣,从某大学随机抽取男生、女生各人,对冰壶运动有兴趣的人数占总数的,女生中有人对冰壶运动没有兴趣.
(1)按性别用分层抽样的方法从对冰壶运动有兴趣的学生中,抽取人作为冰壶运动的宣传员,求男生、女生各选多少人?
(2)完成下面列联表,并判断是否有的把握认为对冰壶运动是否有兴趣与性别有关?
有兴趣
没有兴趣
合计
男
女
合计
附:
0.100
0.050
0.025
0.010
0.001
2.706
3.841
5.024
6.635
10.828
【答案】(1)男生选人,女生选人.
(2)有的把握认为对冰壶运动是否有兴趣与性别有关.
【分析】对于小问1,由题意计算对冰壶感兴趣的男女生人数,根据其比例,再分别计算抽取的人中男女生人数;
对于小问2,完成列联表,代入,计算其近似值,与比较大小,进行判断.
(1)
对冰壶运动感兴趣的人数为人,女生中有人对冰壶运动没有兴趣,
所以女生中有人对冰壶运动有兴趣,所以男生中有人对冰壶运动有兴趣,
按性别用分层抽样的方法从对冰壶运动有兴趣的学生中,抽取人作为冰壶运动的宣传员,
其中抽取的男生为人,女生为人,即男生选人,女生选人.
(2)
由题意,完成下面列联表如下
有兴趣
没有兴趣
合计
男
150
50
200
女
120
80
200
合计
270
130
400
,
所以有的把握认为对冰壶运动是否有兴趣与性别有关.
14.(四川省雅安市2023届高三零诊考试数学(文)试题)某地区对高一年级学生进行体质健康测试(简称体测),现随机抽取了900名学生的体测结果等级(“良好及以下”或“优秀”)进行分析.得到如下列联表:
良好及以下
优秀
合计
男
450
200
650
女
150
100
250
合计
600
300
900
(1)计算并判断是否有99%的把握认为本次体测结果等级与性别有关系?
(2)事先在本次体测等级为“优秀”的学生中按照性别采用分层抽样的方式随机抽取了6人.若从这6人中随机抽取2人对其体测指标进一步研究,求抽到的2人中至少有1名女生的概率.
附表及公式:
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
其中,.
【答案】(1)有99%的把握认为本次体测结果等级与性别有关系
(2)
【分析】(1)按由题可得,进而即得;
(2)利用列举法结合古典概型概率公式即得。
【详解】(1)由题可得,
故有99%的把握认为本次体测结果等级与性别有关系;
(2)由题可得所抽取的6名学生中女生2人,记为,,男生4人,记为,,,.
从这6人中选取2人的所有基本事件有:,,,,,,,
,,,,,,,,共15个.
其中至少有一名女生的基本事件,,,,,,,,,有9个.
所以,抽到的2人中至少有1名女生的概率.
15.(四川省宜宾市2023届高三上学期第一次诊断性数学(文)数学试题)现有甲、乙、丙三个人相互传接球,第一次从甲开始传球,甲随机地把球传给乙、丙中的一人,接球后视为完成第一次传接球;接球者进行第二次传球,随机地传给另外两人中的一人,接球后视为完成第二次传接球;依次类推,假设传接球无失误.
(1)设第一次接球人为,第二次接球人为,通过次传接球后,列举出的所有可能的结果;
(2)完成第三次传接球后,计算球正好在乙处的概率.
【答案】(1)答案见解析
(2)
【分析】(1)由题意直接列举出基本事件即可;
(2)利用列举法结合古典概型的概率公式求解即可
【详解】(1)通过次传接球后,的结果:
(乙,甲),(乙,丙),(丙,甲),(丙,乙);
(2)三次传接球,接球的结果:
(乙,甲,乙),(乙,甲,丙),(乙,丙,甲),(乙,丙,乙),
(丙,甲,乙),(丙,甲,丙),(丙,乙,甲),(丙,乙,丙),
共8种,它们是等可能的,
其中球正好在乙处的结果有:(乙,甲,乙),(乙,丙,乙),(丙,甲,乙),共3种,
所以第3次传接球后,球正好在乙处的概率为
16.(四川省达州市2023届高三第一次诊断测试模拟考试文科数学试题)第24届冬季奥林匹克运动会于2022年2月在中国北京举行.为迎接此次冬奥会,北京市组织大学生开展冬奥会志愿者的培训活动,并在培训结束后统一进行了一次考核.为了了解本次培训活动的效果,从A,B两所大学各随机抽取10名学生的考核成绩,并作出如图所示的茎叶图.
(1)计算A,B两所大学学生的考核成绩的平均值;
(2)将学生的考核成绩分为两个等级,如下表所示.现从样本考核等级为优秀的学生中任取2人,求2人来自同一所大学的概率.
考核成绩
考核等级
合格
优秀
【答案】(1),.
(2).
【分析】(1)根据平均数的计算方法求得平均数.
(2)利用列举法,结合古典概型概率计算公式求得所求概率.
【详解】(1),
.
(2)记事件为“从样本考核等级为优秀的学生中任取2人,2人来自同一所大学”.
样本中,校考核等级为优秀的学生共有3人,分别记为,
校考核等级为优秀的学生共有3人,分别记为,
从这6人中任取2人,所有的基本事件为:
,共15个,
而事件包含的基本事件是,共6个,
因此.
17.(四川省成都市石室中学2021-2022学年高三下学期“三诊模拟”文科数学试题)某学校共有1000名学生参加知识竞赛,其中男生400人.为了了解该校学生在知识竞赛中的情况,采取按性别分层抽样,随机抽取了100名学生进行调查,分数分布在450~950分之间.将分数不低于750分的学生称为“高分选手”.根据调查的结果绘制的学生分数频率分布直方图如图所示.
(1)求a的值,并估计该校学生分数的众数、平均数和中位数(同一组中的数据用该组区间的中点值作代表);
(2)若样本中属于“高分选手”的女生有10人,完成下列2×2列联表,并判断是否有97.5%的把握认为该校学生属于“高分选手”与“性别”有关.
属于“高分选手”
不属于“高分选手”
合计
男生
女生
合计
参考公式:,其中.
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
【答案】(1)见解析
(2)填表见解析;有
【分析】(1)由频率和为1可得a值,由直方图中众数、平均数和中位数的计算公式进行计算即可;
(2)由题意得到2×2列联表,然后计算的观测值,然后与题目中表格的数据进行比较即可得到结论.
【详解】(1),解得.
众数估计值为600分.
平均数估计值为(分)
分数分布在450~650分之间时,频率为,
故中位数估计值为650分.
(2)由题意可知,样本中男生有40人,女生有60人,属于“高分选手”的有25人,其中女生10人.
因此,得到2×2列联表如下:
属于高分选手
不属于高分选手
合计
男生
15
25
40
女生
10
50
60
合计
25
75
100
因此,的观测值,
所以有97.5%的把握认为该校学生属于“高分选手”与“性别”有关.
18.(浙江省嘉兴市2022-2023学年高三上学期9月基础测试数学试题)某市决定利用两年时间完成全国文明城市创建的准备工作,其中“礼让行人”是交警部门主扲的重点工作之一.“礼让行人”即当机动车行经人行横道时应当减速慢行,遇行人正在通过人行横道,应当停车让行.如表是该市某一主干路口电子监控设备抓拍的今年1-6月份机动车驾驶员不“礼让行人”行为的人数统计数据.
月份
1
2
3
4
5
6
不“礼让行人”
33
36
40
39
45
53
(1)请利用所给的数据求不“礼让行人”人数与月份之间的经验回归方程,并预测该路口今年11月份不“礼让行人”的机动车驾驶员人数(精确到整数);
(2)交警部门为调查机动车驾驶员“礼让行人”行为与驾龄满3年的关系,从这6个月内通过该路口的机动车驾驶员中随机抽查了100人,如表所示:
不“礼让行人”
礼让行人
驾龄不超过3年
18
42
驾龄3年以上
4
36
依据小概率值的独立性检验,能否据此判断机动车驾驶员“礼让行人”行为与驾龄满3年有关?并说明理由.
附:参考公式:
,,其中.
独立性检验临界值表:
0.10
0.05
0.010
0.005
0.001
2.706
3.841
6.635
7.879
10.828
【答案】(1),68人
(2)认为“礼让行人”与驾龄满3年有关,且推断犯错误的概率不超过0.05,理由见解析
【分析】(1)利用表中的数据和公式直接求解即可,
(2)先完成列联表,然后利用公式求解,再根据临界值分析判断.
【详解】(1)由表中数据可知:,,
所以,即,
所以,
所求得经验回归方程为.
当时,,
所以预测该路口11月份的不“礼让行人”违章驾驶员人数为68人.
(2)零假设为:“礼让行人”与驾龄满3年无关,
由题意知列联表为
不礼让行人
礼让行人
合计
驾龄不超过3年
18
42
60
驾龄3年以上
4
36
40
合计
22
78
100
由表中数据可得
根据小概率值的独立性检验,我们推新不成立,
即认为“礼让行人”与驾龄满3年有关,且推断犯错误的概率不超过0.05,
19.(四川省内江市2023届高三第一次模拟考试数学(理)试题)第届北京冬季奥林匹克运动会于年月日至月日在北京和张家口联合举办.这是中国历史上第一次举办冬季奥运会,它掀起了中国人民参与冬季运动的大热潮.某中学共有学生:名,其中男生名,女生名,按性别分层抽样,从中抽取名学生进行调查,了解他们是否参与过滑雪运动.情况如下:
参与过滑雪
未参与过滑雪
男生
女生
(1)若,,求参与调查的女生中,参与过滑雪运动的女生比未参与过滑雪运动的女生多的概率;
(2)若参与调查的女生中,参与过滑雪运动的女生比未参与过滑雪运动的女生少人,试根据以上列联表,判断是否有的把握认为“该校学生是否参与过滑雪运动与性别有关”.
附:
,.
【答案】(1)
(2)没有的把握认为“该校学生是否参与过滑雪运动与性别有关”
【分析】(1)根据分层抽样原则可确定抽取的名学生中,女生有人,由此可列举出所有可能的取值结果,并确定的取值结果,根据古典概型概率公式可求得结果;
(2)根据可求得的值,进而得到,由列联表可求得,对比临界值表可得结论.
【详解】(1)根据分层抽样原则知:抽取的名学生中,女生有人,
若,,则所有可能的取值结果有,,,,,,,,,共个;
其中满足的有,,,,共个,
参与过滑雪运动的女生比未参与过滑雪运动的女生多的概率为.
(2)由(1)知:,又,,,
,
,
没有的把握认为“该校学生是否参与过滑雪运动与性别有关”.
20.(四川省绵阳市2023届高三上学期第二次诊断性测试理科数学试题)某县依托种植特色农产品,推进产业园区建设,致富一方百姓.已知该县近年人均可支配收入如下表所示,记年为,年为,…以此类推.
年份
年份代号
人均可支配收入(万元)
(1)使用两种模型:①;②的相关指数分别约为,,请选择一个拟合效果更好的模型,并说明理由;
(2)根据(1)中选择的模型,试建立关于的回归方程.(保留位小数)
附:回归方程中斜率和截距的最小二乘估计公式分别为,.
参考数据:,令,.
【答案】(1)应选择
(2)
【分析】(1)根据越大,模型拟合效果越好,可确定所选模型;
(2)令,利用最小二乘法可求得,进而得到回归方程.
【详解】(1),根据统计学知识可知:越大,模型拟合效果越好,
应选择模型.
(2)令,
,,
,
又,
,,
关于的回归方程为.
21.(四川省德阳市2023届高三第一次诊断考试数学(文)试题)买盲盒是当下年轻人的潮流之一,每个系列的盲盒分成若干个盒子,每个盒子里面随机装有一个动漫、影视作品的图片,或者设计师单独设计出来的玩偶,消费者不能提前得知具体产品款式,具有随机属性,某礼品店2022年1月到8月售出的盲盒数量及利润情况的相关数据如下表所示:
月份/月
1
2
3
4
5
6
7
8
月销售量/百个
4
5
6
7
8
10
11
13
月利润/千元
4.1
4.6
4.9
5.7
6.7
8.0
8.4
9.6
(1)求出月利润y(千元)关于月销售量x(百个)的回归方程(精确到0.01);
(2)2022年“一诊”考试结束后,某班数学老师购买了装有“五年高考三年模拟”和“教材全解”玩偶的两款盲盒各3个,从中随机选出3个作为礼物赠送给同学,求3个盲盒中装有“五年高考三年模拟”玩偶的个数至少为2个的概率.
参考公式:回归方程中斜率和截距最小二乘估计公式分别为:,.
参考数据:,.
【答案】(1)
(2)
【分析】(1)将表格数据代入公式,计算回归方程;
(2)列举从6个盲盒中抽取3个的所有结果,由所有基本事件个数和“五年高考三年模拟”玩偶个数至少为2个的基本事件个数,求得概率.
【详解】(1)由题,,
,
所以,,
,,
所以回归方程为.
(2)记装有“五年高考三年模拟”玩偶的3个盲盒为,,,
记装有“教材全解”玩偶的3个盲盒为,,,
从中选出3个,共有:,,,,
,,,,,,
,,,,,,
,,,共20个基本事件,
其中,“五年高考三年模拟”玩偶个数至少为2个的基本事件有10个,
故所求事件发生的概率.
22.(四川省成都市2023届高三第一次诊断性检测数学(文科)试题)成都作为常住人口超2000万的超大城市,注册青年志愿者人数超114万,志愿服务时长超268万小时.2022年6月,成都22个市级部门联合启动了2022年成都市青年志愿服务项目大赛,项目大赛申报期间,共收到331个主体的416个志愿服务项目,覆盖文明实践、社区治理与邻里守望、环境保护等13大领域.已知某领域共有50支志愿队伍申报,主管部门组织专家对志愿者申报队伍进行评审打分,并将专家评分(单位:分)分成6组:,得到如图所示的频率分布直方图.
(1)求图中的值;
(2)已知评分在的队伍有4支,若从评分在的队伍中任选两支队伍,求这两支队伍至少有一支队伍评分不低于85分的概率.
【答案】(1)
(2)
【分析】(1)利用直方图中各矩形面积和为1列方程求解即可;
(2)由直方图求得不低于90分的队伍有2支,评分在的队伍有2支.评分在分的队伍有6支,再利用列举法可得两支队伍至少有一支队伍评分不低于85分的概率.
【详解】(1)由,
解得.
(2)由题意知不低于90分的队伍有支,故评分在的队伍有2支.
评分在分的队伍有支.
记评分落在的4支队伍为;评分落在的2支队伍为,.
则从评分在的队伍中任选两支队伍的基本事件有:,,,共15个.
其中两支队伍至少有一支队伍评分不低于85分的基本事件有:,,共9个.
故所求概率为.
23.(四川省泸州市2022届高三第二次教学质量诊断性考试文科数学试题)某县充分利用自身资源,大力发展优质李子树种植项目.该县农科所为了对比A,B两种不同品种脆红李的产量,各选20块试验田分别种植了A,B两种脆红李,所得的20个亩产数据(单位:100)都在内,根据亩产数据得到频率分布直方图如下图:
(1)从B种脆红李亩产量数据在内任意抽取2个数据,求抽取的2个数据都在内的概率;
(2)根据频率分布直方图,用平均亩产量判断应选择种植A种还是B种脆红李,并说明理由.
【答案】(1)
(2)应选择种植B种脆红李,理由见解析.
【分析】(1)种脆红李亩产量数据在,内的有5个,其中数据在,的有2个,数据在,的有3个,从种脆红李亩产量数据在,内任意抽取2个数据,基本事件总数,抽取的2个数据都在,内包含的基本事件个数,由此能求出抽取的2个数据都在,内的概率;(2)根据频率分布直方图,分别求出A种脆红李平均亩产量和种脆红李平均亩产量,从而得到用平均亩产量来判断应选择种植种脆红李.
【详解】(1)(1)种脆红李亩产量数据在,内的有:
,
其中数据在,的有:个,
数据在,的有:个,
从B种脆红李亩产量数据在,内任意抽取2个数据,
基本事件总数,
抽取的2个数据都在,内包含的基本事件个数,
抽取的2个数据都在,内的概率为.
(2)根据频率分布直方图,
种脆红李的平均亩产量为:
,
B种脆红李的平均亩产量为:
,
A种脆红李平均亩产量小于B种脆红李的平均亩产量,
用平均亩产量来判断应选择种植B种脆红李.
24.(四川省南充市2022届高考适应性考试(二诊)文科数学试题)从某食品厂生产的面包中抽取100个,测量这些面包的一项质量指标值,由测量结果得如下频数分布表:
质量指标值分组
频数
8
22
36
28
6
(1)在相应位置上作出这些数据的频率分布直方图;
(2)估计这种面包质量指标值的平均数(同一组中的数据用该组区间的中点值作代表).
(3)根据以上抽样调查数据,能否认为该食品厂生产的这种面包符合“质量指标值不低于85的面包至少要占全部面包的规定”?
【答案】(1)答案见解析
(2)
(3)能
【分析】(1)根据频数分布表,计算每组的频率,即可绘制频率分布直方图;
(2)根据频率分布直方图,按照平均数的求法求得答案;
(3)计算质量指标值不低于85的面包所占比例即可得答案.
(1)
(2)
质量指标值的样本平均数为
,
所以这种面包质量指标值的平均数的估计值为
(3)
质量指标值不低于85的面包所占比例为,
由于该值大于,故可以认为该食品厂生产的这种面包符合“质量指标值不低于85的面包至少要占全部面包的规定”.
25.(四川省成都市2022届高三第二次诊断性检测文科数学试题)某中学为研究课外阅读时长对语文成绩的影响,随机调查了50名学生某阶段每人每天课外阅读的平均时长(单位:分钟)及他们的语文成绩,得到如下的统计表:
平均时长(单位:分钟)
(0,20]
(20,40]
(40,60]
(60,80]
人数
9
21
15
5
语文成绩优秀人数
3
9
10
3
(1)估算该阶段这50名学生每天课外阅读平均时长的平均数(同一组中的数据用该组区间的中点值为代表);
(2)若从课外阅读平均时长在区间(60,80]的学生中随机选取3名进行研究,求所选3名学生中至少有2名语文成绩优秀的学生的概率.
【答案】(1)平均数为分钟
(2)
【分析】(1)根据平均数的求法,求得平均数.
(2)利用列举法,结合古典概型的概率计算公式,计算出所求概率.
(1)
平均数为分钟.
(2)
区间(60,80]的学生有人,记为,其中为语文成绩优秀,
从中任取人,基本事件有:,共种,
其中至少有人语文成绩优秀的为:,共种,
所以所选3名学生中至少有2名语文成绩优秀的学生的概率为.
26.(四川省德阳市2022届高三“三诊”数学(文科)试题)第24届冬季奥林匹克运动会于2022年2月4日在中国北京开幕,简称“北京冬奥会”.某媒体通过网络随机采访了某市100名关注“北京冬奥会”的市民,其年龄数据绘制成如图所示的频率分布直方图.
(1)已知[30,40)、[40,50)、[50,60)三个年龄段的人数依次成等差数列,求的值;
(2)该媒体将年龄在[30,50)内的人群定义为高关注人群,其他年龄段的人群定义为次高关注人群,为了进一步了解其关注项目.现按“关注度的高低”采用分层抽样的方式从参与采访的100位关注者中抽取5人,并在这5人中随机抽取2人进行电视访谈,求此2人中恰好来自高关注人群和次高关注人群各一人的概率.
【答案】(1)
(2)
【分析】(1)根据已知和所有矩形面积之和等于1列方程组,求解可得;
(2)先根据分层抽样求出高关注人群和次高关注人群各有多少人,然后直接列举出所有结果可得.
(1)
在[30,40)、[40,50)、[50,60)三个年龄段的人数依次为:
,,
由题意知,…①
又,即…②
由①②联立求解得:
(2)
年龄在[30,50)内的人数为
采用分层抽样的方式从参与采访的100位关注者中抽取5人,则抽取到的高关注人3人,记为a,b,c,抽取到次高关注人2人,记为1,2.则从这5人中随机抽取2人的所用结果为:
,共10种,其中来自高关注人群和次高关注人群各一人共有6种,
所以,从这5人中随机抽取2人进行电视访谈,求此2人中恰好来自高关注人群和次高关注人群各一人的概率为
27.(四川省眉山市2022届高中第三次诊断性考试数学(文史类)试题)新冠疫苗有三种类型:腺病毒载体疫苗、灭活疫苗和重组蛋白亚单位疫苗,腺病毒载体疫苗只需要接种一针即可产生抗体,适合身体素质较好的青壮年,需要短时间内完成接种的人群,突发聚集性疫情的紧急预防.灭活疫苗和重组蛋白亚单位疫苗安全性高,适合老、幼、哺、孕及有慢性基础病患者和免疫缺陷人群,灭活疫苗需要接种两次.重组蛋白亚单位新冠疫苗需要完成全程三针接种,接种第三针后,它的有效保护作用为90%,人体产生的抗体数量提升5-10倍,甚至更高(即接种疫苗第三针后,有90%的人员出现这种抗疫效果).以下是截止2021年12月31日在某县域内接种新冠疫苗人次(单位:万人,忽略县外人员在本县接种情况)统计表:
腺病毒载体疫苗
灭活疫苗
重组蛋白亚单位疫苗
第一针
0.5
10
110
第二针
0
10
110
第三针
0
0
100
其中接种腺病毒载体疫苗的统计情况如下:
接种时间
接种原因
接种人次(单位:人)
3月
疫情突发
1500
6月
高考考务
1000
7月
抗洪救灾
2500
(1)遭遇3月疫情突发、服务6月高考考务、参加7月抗洪救灾的人都是不同的人,在已接种腺病毒载体疫苗的人员中随机抽取一名,求这个人参加了抗洪救灾的概率;
(2)在已接种灭活疫苗和重组蛋白亚单位疫苗的人员中,以人体产生的抗体数量是否至少提升5-10倍为依据,用分层抽样的方法抽取4人,再从这4人随机抽取2人,求这2人均为人体产生的抗体数量至少提升5-10倍的疫苗接种者的概率.
【答案】(1)
(2)
【分析】(1)参加了抗洪救灾的接种人数为2500,总接种腺病毒载体疫苗的人数有5000,根据古典概型即可求解;
(2)接种灭活疫苗和重组蛋白亚单位疫苗人次共有120万人,接种灭活疫苗和重组蛋白亚单位疫苗人次共有120万人,比率为,所以抽取4人中有1人人体产生的抗体数量不足以提升5-10倍,由列举法即可求解结果.
【详解】(1)在已接种腺病毒载体疫苗的人员中随机抽取一名,这个人参加了抗洪救灾的概率为
;
(2)截止2021年12月31日在某县域内接种灭活疫苗和重组蛋白亚单位疫苗人次共有120万人
其中接种灭活疫苗有10万人,接种重组蛋白亚单位疫苗有110万人,这110万人中只有100
万人接种了第三针,根据有效保护率只有90万人人体产生的抗体数量至少提升5-10倍,
比率为.所以以人体产生的抗体数量是否至少提升5-10倍为依据,用分层抽样的方
法抽取4人,有1人人体产生的抗体数量不足以提升5-10倍,3人人体产生的抗体数量至少
提升5-10倍.
设抽取4人中不足以提升5-10倍的那个人为,其他3人分别为故从这4人中
随机抽取2人,所有可能结果分别为共有6个结果,其中
2人均为人体产生的抗体数量至少提升5-10倍的疫苗接种者的结果有共有
3个结果.
所以2人均为人体产生的抗体数量至少提升5-10倍的疫苗接种者的概率为.
28.(四川省成都市2022届高三第三次诊断考试文科数学试题)某中学为增强学生的环保意识,举办了“爱成都,护环境”的知识竞赛活动,为了解本次知识竞赛活动参赛学生的成绩,从中抽取了n名学生的分数(得分取正整数,满分为100分,所有学生的得分都在区间中)作为样本进行统计.按照,,,,的分组作出如下的频率分布直方图,并作出下面的样本分数茎叶图(图中仅列出了得分在,的数据).
(1)求样本容量n和频率分布直方图中x、y的值;
(2)在选取的样本中,从竞赛成绩不低于80分的三组学生中按分层抽样抽取了5名学生,再从抽取的这5名学生中随机抽取2名学生到天府广场参加环保知识宣传活动,求这2名学生的分数都在中的概率.
【答案】(1)n=40,,;
(2)﹒
【分析】(1)根据茎叶图中成绩在的频数和频率频率分布直方图中的频率即可求出n,再结合茎叶图中的频数可求频率分布直方图中x,根据频率总和为1即可求y.
(2)根据分层抽样求出5名学生中成绩在和的人数,分别编号,列举出从5名学生选出2名的组合,并列举出2名学生分数都在的组合,根据古典概率计算方法即可计算﹒
(1)
由茎叶图可知成绩在中的频数为3.
结合频率分布直方图,得.
∴.
∴.
(2)
由题意,本次竞赛成绩样本中分数在中的学生有名,
分数在中的学生有名,
按分层抽样抽取的5名学生中,分数在中的学生有名,记为a、b、c;分数在中的学生有名,记为1、2.
从这5名学生中随机选取2名学生的所有结果为,共10种.
其中2名学生的分数都在中的结果为,共3种.
∴所选2名学生的分数都在中的概率.
29.(四川省凉山州2022届高三第三次诊断性检测数学(文科)试题)2022年,举世瞩目的冬奥会在北京举行,冬奥会吉祥物“冰墩墩”和“雪容融”有着可爱的外表和丰富的寓意,自亮相以来就好评不断,深受各国人民的喜爱.某市一媒体就本市小学生是否喜爱这两种吉祥物对他们进行了一次抽样调查,列联表如下:(单位:人)
喜爱
不喜爱
合计
男生
30
20
50
女生
40
10
50
合计
70
30
100
(1)根据列联表及参考公式和数据,能否在犯错误的概率不超过2.5%的前提下,认为是否喜爱吉祥物与性别有关?
(2)现从样本中按性别分层抽样的方法取出6人,再从这6人中随机抽取3人,求抽取的3人中至多1人是女生的概率
参考数据及公式:,其中
参考数据:
0.15
0.10
0.05
0.025
0.010
2.072
2.706
3.841
5.024
6.635
【答案】(1)不能
(2)
【分析】(1)先由公式求出,与参考数据比较,得出答案.
(2)利用分层抽样计算出男女生人数,再由古典概型及组合的知识得出答案.
(1)
所以,不能在犯错概率不超过2.5%的前提下,认为是否喜爱吉祥物与性别有关.
(2)
由题意知,按性别分层抽样方法抽取出来的6人中,有男生3人,有女生3人,
所以,抽取的3人中至多1人是女生的概率
30.(四川省遂宁市绿然国际学校2022届高考数学(文科)二诊模拟试题)为弘扬劳动精神,树立学生“劳动最美,劳动最光荣”的观念,某校持续开展“家庭劳动大比拼”活动某班统计了本班同学月份的人均月劳动时间单位:小时,并建立了人均月劳动时间关于月份的线性回归方程,与的原始数据如表所示:
月份
人均月劳动时间
由于某些原因导致部分数据丢失,但已知.
(1)求,的值;
(2)求该班月份人均月劳动时间数据的残差值残差即样本数据与预测值之差.
参考公式:在线性回归方程中,.
【答案】(1),;
(2).
【分析】(1)由表知,,,由,可得,由回归直线方程恒过样本中心点,可得,再由,得,然后解方程组,即可;
(2)把代入(1)中得到的回归方程,求得预测值后,即可得解.
【详解】(1)由表知,,,
所以,
所以,即,
因为回归直线方程恒过样本中心点,
所以,即,由,得,,
因为,所以,
由,得,.
(2)由(1)知,线性回归方程为,
所以当时,预测值,
此时残差为.
四川省高考数学复习 专题10 圆锥曲线(文科)解答题30题专项提分计划: 这是一份四川省高考数学复习 专题10 圆锥曲线(文科)解答题30题专项提分计划,文件包含四川省高考数学复习专题10圆锥曲线文科解答题30题专项提分计划解析版docx、四川省高考数学复习专题10圆锥曲线文科解答题30题专项提分计划原卷版docx等2份试卷配套教学资源,其中试卷共51页, 欢迎下载使用。
四川省高考数学复习 专题07 统计与概率(理科)解答题30题专项提分计划: 这是一份四川省高考数学复习 专题07 统计与概率(理科)解答题30题专项提分计划,文件包含四川省高考数学复习专题7统计与概率理科解答题30题专项提分计划解析版docx、四川省高考数学复习专题7统计与概率理科解答题30题专项提分计划原卷版docx等2份试卷配套教学资源,其中试卷共69页, 欢迎下载使用。
四川省高考数学复习 专题06 立体几何(文科)解答题30题专项提分计划: 这是一份四川省高考数学复习 专题06 立体几何(文科)解答题30题专项提分计划,文件包含四川省高考数学复习专题6立体几何文科解答题30题专项提分计划解析版docx、四川省高考数学复习专题6立体几何文科解答题30题专项提分计划原卷版docx等2份试卷配套教学资源,其中试卷共60页, 欢迎下载使用。












