专题12 球的外接、内切及立体几何最值问题——2022-2023学年高一数学下学期期末知识点精讲+训练学案+期末模拟卷（苏教版2019必修第二册）

这是一份专题12 球的外接、内切及立体几何最值问题——2022-2023学年高一数学下学期期末知识点精讲+训练学案+期末模拟卷（苏教版2019必修第二册），文件包含专题12球的外接内切及立体几何最值问题解析版docx、专题12球的外接内切及立体几何最值问题原卷版docx等2份学案配套教学资源，其中学案共45页， 欢迎下载使用。
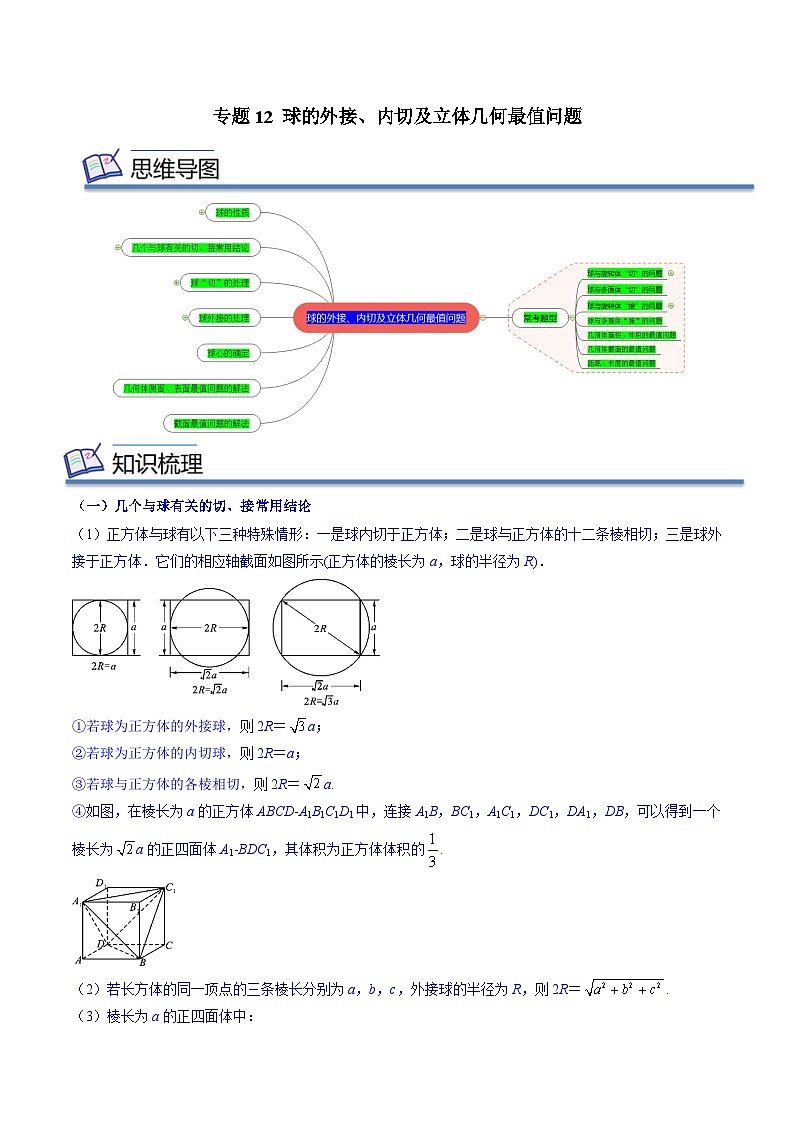
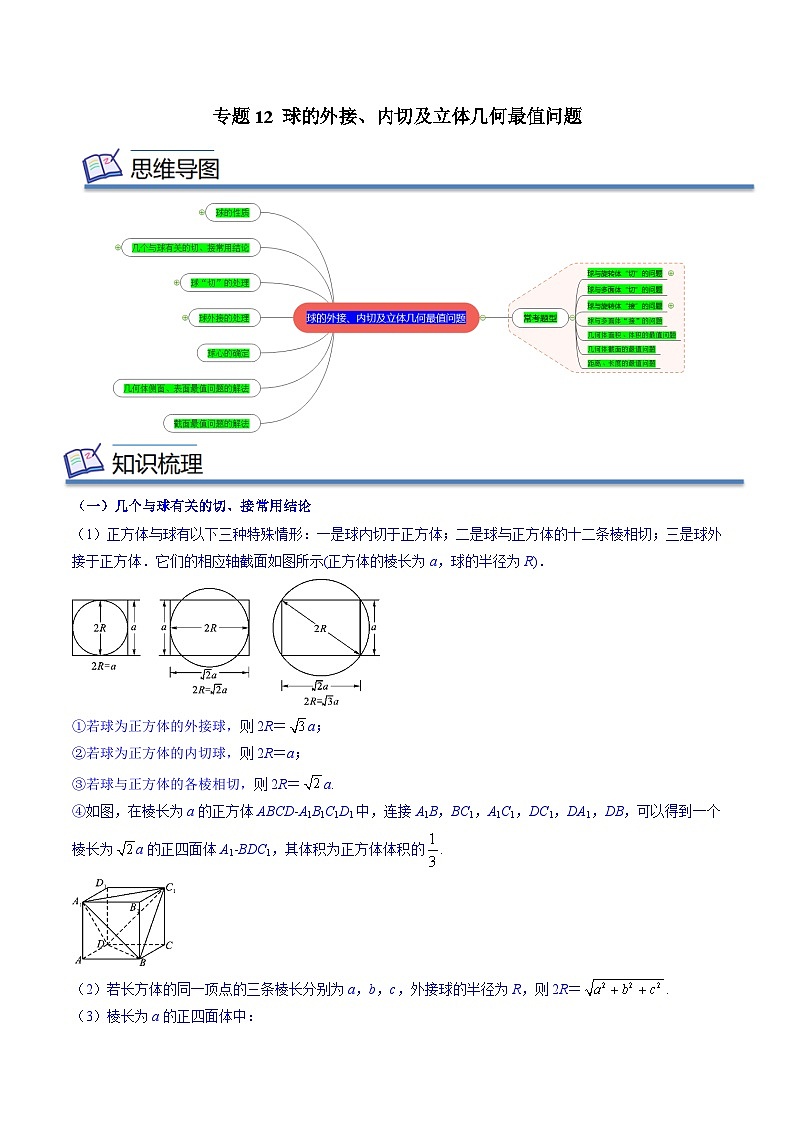
专题12 球的外接、内切及立体几何最值问题               （一）几个与球有关的切、接常用结论（1）正方体与球有以下三种特殊情形：一是球内切于正方体；二是球与正方体的十二条棱相切；三是球外接于正方体．它们的相应轴截面如图所示(正方体的棱长为a，球的半径为R)．①若球为正方体的外接球，则2R＝a；②若球为正方体的内切球，则2R＝a；③若球与正方体的各棱相切，则2R＝a.④如图，在棱长为a的正方体ABCD­A1B1C1D1中，连接A1B，BC1，A1C1，DC1，DA1，DB，可以得到一个棱长为a的正四面体A1­BDC1，其体积为正方体体积的.（2）若长方体的同一顶点的三条棱长分别为a，b，c，外接球的半径为R，则2R＝.（3）棱长为a的正四面体中：①斜高为a；②高为a；③对棱中点连线长为a；④外接球的半径为a；⑤内切球的半径为a；⑥ S表面积＝a2；⑦ V＝a3；⑧相邻两个面的二面角：cos α＝；⑨三条侧棱与底面的夹角：cos β＝；⑩正四面体的外接球与内切球的半径之比为3∶1.（二）球“切”的处理1．解决与球有关的内切问题主要是指球内切于多面体或旋转体，解答时首先要找准切点，通过作截面来解决．如果内切的是多面体，则作截面时主要抓住多面体过球心的对角面来作．2．几何体内切球问题的处理(1)解题时常用以下结论确定球心和半径：①球心在过切点且与切面垂直的直线上；②球心到各面距离相等．(2)利用体积法求多面体内切球半径，.(3)在求四面体内切球的半径时,应重视分割的思想方法,即将该四面体分割为以球心为顶点,各面为底面的四个三棱锥,通过其体积关系求得半径.（三）球外接的处理1．把一个多面体的几个顶点放在球面上即为球的外接问题．解决这类问题的关键是抓住外接的特点，即球心到多面体的顶点的距离等于球的半径．2．（1）确定球心和半径解题思维流程： (R—球半径，r—截面圆的半径，h—球心到截面圆心的距离)．注：若截面为非特殊三角形可用正弦定理求其外接圆半径 r. (2)三条侧棱两两垂直的三棱锥，可以补成长方体，它们是同一个外接球． 注意：不共面的四点确定一个球面．(3)求解球的内接正方体、长方体等问题的关键是把握球的直径即是几何体的体对角线.(4)若球面上四点P,A,B,C的连线中PA,PB,PC两两垂直或三棱锥的三条侧棱两两垂直,则可构造长方体或正方体解决问题.3.球与旋转体的组合通常作出它们的轴截面解题;球与多面体的组合,一般通过多面体的一条侧棱和球心,并结合“切点”或“接点”作出截面图,把空间问题化归为平面问题求解.（四）球心的确定1．由球的定义确定球心若一个多面体的各顶点都在一个球的球面上，则称这个多面体是这个球的内接多面体，这个球是这个多面体的外接球．也就是说如果一个定点到一个简单多面体的所有顶点的距离都相等，那么这个定点就是该简单多面体外接球的球心．①长方体或正方体的外接球的球心是其体对角线的中点；②正三棱柱的外接球的球心是上、下底面中心连线的中点；③直三棱柱的外接球的球心是上、下底面三角形外心连线的中点；④正棱锥的外接球的球心在其高上，具体位置可通过建立直角三角形运用勾股定理计算得到．2．构造长方体或正方体确定球心①正四面体、三条侧棱两两垂直的正三棱锥、四个面都是直角三角形的三棱锥，可将三棱锥补成长方体或正方体；②同一个顶点上的三条棱两两垂直的四面体、相对的棱相等的三棱锥，可将三棱锥补成长方体或正方体；③若已知棱锥含有线面垂直关系，则可将棱锥补成长方体或正方体；④若三棱锥的三个侧面两两垂直，则可将三棱锥补成长方体或正方体．3．由球的性质确定球心①球的截面均为圆面；②球心和截面圆心的连线垂直于该截面，则有.（五）几何体侧面、表面最值问题的解法(1)观察图形特征，确定取得最值的条件，计算最值． (2)设出未知量建立函数关系，利用基本不等式计算最值．(3)几何体表面两点间距离(路程)最小问题，“展平”处理．（六）截面最值问题的解法（1）建立函数模型求最值问题：①设元；②建立二次函数模型；③求最值．（2）猜想法求最值问题：要灵活运用一些特殊图形与几何体的特征，“动中找静”，如正三角形、正六边形、正三棱锥等．　题型一  球与旋转体“切”的问题【典例1】（江西省2023届高三教学质量监测数学（理）试题）在炎热的夏天里，人们都喜欢在饮品里放冰块.如图是一个高脚杯，它的轴截面是正三角形，容器内有一定量的水.若在高脚杯内放入一个球形冰块后，冰块没有开始融化前水面所在的平面恰好经过冰块的球心（水没有溢出），则原来高脚杯内水的体积与球的体积之比是（    ）A．1 B． C． D．【典例2】（2023·河北石家庄·统考一模）已知圆台的上､下底面圆的半径之比为，侧面积为，在圆台的内部有一球，该球与圆台的上､下底面及母线均相切，则球的表面积为（    ）A． B． C． D．【总结提升】1.利用几何体特征；2.利用旋转体的轴截面.题型二  球与多面体“切”的问题【典例3】（2023·全国·模拟预测）已知三棱锥的所有棱长均为2，若球经过三棱锥各棱的中点，则球的表面积为（    ）A． B． C． D．【典例4】（2022秋·广东肇庆·高三肇庆市第一中学校考阶段练习）已知正三棱锥的侧棱长为，底面边长为，则它的内切球的半径为（    ）A． B． C． D．【典例5】（2023·青海·校联考模拟预测）已知体积为的球与正三棱柱的所有面都相切，则三棱柱外接球的表面积为（    ）A． B． C． D．题型三  球与旋转体“接”的问题【典例6】（2022秋·重庆渝中·高三重庆巴蜀中学校考阶段练习）圆台上､下底面圆的圆周都在一个半径为5的球面上，其上､下底面圆的周长分别为和，则该圆台的侧面积为（    ）A． B． C． D．【典例7】（2023春·广东广州·高一广州市天河中学校考阶段练习）已知圆锥的侧面展开图是一个半径为的半圆，则圆锥的底面半径为______；若该圆锥的顶点及底面圆周在球O的表面上，则球O的体积为______.【典例8】（2022秋·江苏·高三校联考阶段练习）已知圆柱的轴截面是边长为8的正方形，是圆上两点，是圆上两点，且，则四面体的外接球的表面积为______，四面体的体积为______.题型四  球与多面体“接”的问题【典例9】（2023·四川凉山·二模）在四面体中，，则四面体外接球表面积是（    ）A． B． C． D．【典例10】（2023春·辽宁朝阳·高二北票市高级中学校考阶段练习）如图，在直三棱柱的侧面展开图中，B，C是线段AD的三等分点，且．若该三棱柱的外接球O的表面积为12π，则_______________．【典例11】（2022秋·河南洛阳·高三孟津县第一高级中学校考阶段练习）已知四棱锥的每个顶点都在球O的球面上，侧面底面，底面为边长为2的正方形，，，则四棱锥外接球的体积为__________.【总结提升】求空间多面体的外接球半径的常用方法：①补形法：侧面为直角三角形，或正四面体，或对棱二面角均相等的模型，可以还原到正方体或长方体中去求解；②利用球的性质：几何体中在不同面均对直角的棱必然是球大圆直径，也即球的直径；③定义法：到各个顶点距离均相等的点为外接球的球心，借助有特殊性底面的外接圆圆心，找其垂线，则球心一定在垂线上，再根据带其他顶点距离也是半径，列关系求解即可；题型五  几何体面积、体积的最值问题【典例12】（2023春·重庆沙坪坝·高三重庆八中校考阶段练习）半径均为R的四个球两两之间有且仅有一个公共点，在以四个球心为顶点的三棱锥的内部放一个小球，小球体积的最大值为（    ）A． B． C． D．【数列13】（宁夏吴忠市2023届高三模拟联考）已知表面积为54的正方体的顶点都在球O上，过球心O的平面截正方体所得的截面过正方体相对两棱，的中点F，E，设该截面与及的交点分别为M，N，点P是正方体表面上一点，则以截面EMFN为底面，以点P为顶点的四棱锥的体积的最大值为___________.【典例14】（2023春·浙江宁波·高一余姚中学校考阶段练习）已知某圆锥的内切球的体积为，则该圆锥的表面积的最小值为__________．【典例15】（2022春·山东青岛·高一校考期中）已知正三棱柱的顶点都在同一个半径为的球面上，①当三棱柱的侧棱长等于底面边长时，三棱柱的体积为______，②该三棱柱侧面积的最大值为______．题型六  几何体截面的最值问题【典例16】（2022·全国·高三校联考阶段练习）已知四棱锥P-ABCD的底面ABCD是矩形，且该四棱锥的所有顶点都在球O的球面上，PA⊥平面ABCD, ，点E在棱PB上，且， 过E作球O的截面，则所得截面面积的最小值是____________.【典例17】（2023·河南郑州·统考二模）已知三棱锥P－ABC的各个顶点都在球O的表面上，，，，平面PBC⊥平面ABC，若点E满足，过点E作球O的截面，则所得截面面积的取值范围为______．题型七  距离、长度的最值问题【典例18】（2023·黑龙江哈尔滨·哈尔滨三中校考二模）已知正三棱锥的底面边长为3，侧棱长为，点P为此三棱锥各顶点所在球面上的一点，则点P到平面SAB的距离的最大值为（    ）A． B．C． D．【典例19】（2023春·湖南长沙·高一长郡中学校考阶段练习）如图，直三棱柱中，，，，P为线段上的动点．(1)当P为线段上的中点时，求三棱锥的体积；(2)当P在线段上移动时，求的最小值．一、单选题1．（2023春·江苏南通·高二江苏省如皋中学校考阶段练习）已知三棱锥的棱，，两两垂直，且，．以为直径的球与平面的交线为，则的长度为（      ）A． B． C． D．2．（2022·安徽·校联考二模）在三棱锥中，，则三棱锥外接球的体积为（    ）A． B． C． D．3．（2023·新疆阿克苏·校考一模）长方体中，棱，且其外接球的体积为，则此长方体体积的最大值为（    ）A． B． C． D．4．（2022秋·北京·高三日坛中学校考阶段练习）已知正三棱锥，若平面，则三棱锥的外接球的表面积为（    ）A． B． C． D．二、多选题5．（2023春·浙江宁波·高一余姚中学校考阶段练习）某班级到一工厂参加社会实践劳动，加工出如图所示的圆台，在轴截面中，，且，下列说法正确的有（    ）A．该圆台轴截面面积为B．该圆台的体积为C．该圆台的侧面积为D．沿着该圆台表面，从点到中点的最短距离为6．（云南省2023届高三第一次高中毕业生复习统一检测数学试题）已知三棱锥的四个顶点都在球的球面上，且，，球的表面积为，三棱锥的体积为，记点到平面的距离为，则（    ）A． B．C． D．三、填空题7．（2023·重庆万州·重庆市万州第二高级中学校考模拟预测）已知是圆锥底面圆的直径，圆锥的母线，，则此圆锥外接球的表面积为_________. 8．（2023·全国·高一专题练习）我国古典数学著作《九章算术》中记载，四个面都为直角三角形的四面体称之为鳖臑现有一个“鳖臑”，底面，，且，，，则该四面体的外接球的表面积为________．9．（2022秋·湖南长沙·高二校考期中）棱长为1的正四面体外接球的表面积为______.10．（2022春·福建·高一福建省泉州第一中学校考期中）已知正四棱锥的底面边长为，侧棱长为6，则该四棱锥的外接球的体积为__________．11．（2023·全国·模拟预测）如图，在直三棱柱中，．设D为的中点，三棱锥的体积为，平面平面，则三棱柱外接球的表面积为______．12．（2022秋·河南·高三洛阳市第一高级中学校联考阶段练习）在三棱锥P－ABC中，，AC⊥平面PAB，则三棱锥P－ABC的外接球O的体积为______．13．（2022·全国·高三专题练习）已知四面体的各顶点都在球O的表面上，，E，F分别为的中点，O为的中点．若，直线与所成的角为，，则球O的表面积为____________．14．（2023·河北唐山·开滦第二中学校考一模）已知四棱锥的外接球O的表面积为，四边形ABCD为矩形，M是线段SB的中点，N在平面SCD上，若，，，则球O的体积为______ ，MN的最小值为______ .四、解答题15．（2022春·浙江宁波·高一校联考期中）如图，正三棱锥中，，点分别为的中点，一只蚂蚁从点出发，沿三棱锥侧面爬行到点，求：(1)该三棱锥的体积与表面积；(2)蚂蚁爬行的最短路线长.16．（2023春·河南·高三校联考阶段练习）如图，在四棱锥中，底面四边形ABCD为矩形，，平面ABCD，H为DC的中点．(1)求证：平面平面POC；(2)求三棱锥体积的最大值．