2023年吉林省中考考前冲刺+数学试题（三）(含答案)

这是一份2023年吉林省中考考前冲刺+数学试题（三）(含答案)，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
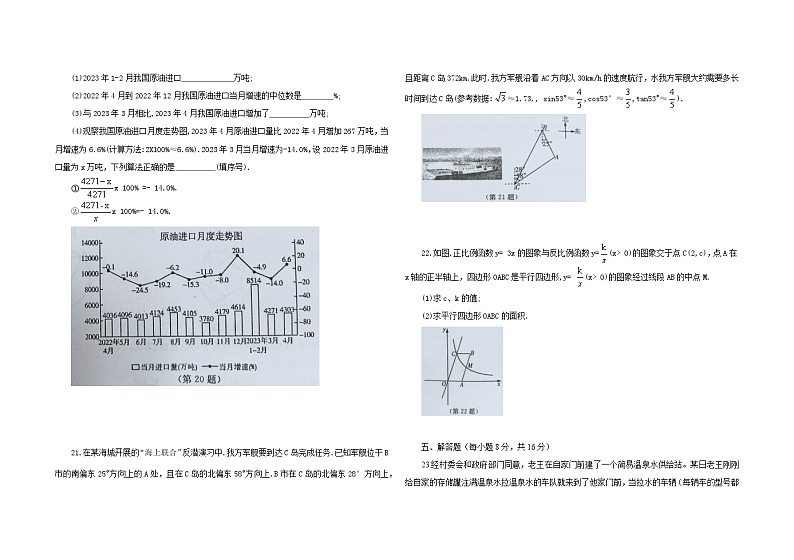
2023年吉林省中考考前冲刺 数学试题（三）满分120分   考试时间为120分钟 一、选择题(每小题2分,共12分)1.在实数1,-1，0， -中，最小的数是（    ）A. -         B.- 1         C.0            D.12.2023年吉林省旅游项目春季集中开工活动在全省各地同时举行,本次参与全省集中开工的旅游项目达到72个,其中,新建项目14个,续建项目58个，总投资1083亿元，将1083亿用科学记数法表示为(     )A.1. 083 X 1010      B.1. 083X 1011    C. 1.083X 1012    D.0.1083X 1017 3.如图所示的几何体的主视图是（    ）4.不等式3+2x< 1的解集在数轴上表示正确的是（     ）5.如图所示的正六边形花环绕它的中心至少旋转a度能与自身重合.则a为(    )A.30          B.60         C.120           D.1806.如图,四边形ABCD内接于⊙0,连接OB、0C.若BC=CD.∠BCO= 59°,则∠A的大小为(    )A.41°         B.52°       C.59°          D.62°二、填空题(每小题3分,共24分)7.分解因式:a2-4=               8.某水果店销僭某种凤梨每千克m元，每周二会员日打7.9折出售，王老师周二购买了10干克这种凤梨共花费               元。9.若关于x的一元二次方程x2+ 3x+n= 0有两个不相等的实数根,则实数n的取值范围是  10.《九章算术》是人类科学史上应用数学的“算经之首”，其中记载了一个有趣的问题:“五只雀、六只燕,共重1斤(古代1斤= 16两)，雀重燕轻,互换其中一只，恰好一样重,问:每只雀、燕的重量各为多少两?”现用列方程组求解，设未知数后,小明列出一个方程为5x+6y= 16,则另一个方程应为                   11.如图，将两个含有30°角的直角三角板的最长边靠在一起滑动，可知直角边AB // CD.其理论依据是                    12.如图,将∆ABC平移到∆DEF的位置，点A的对应点为点D,DE、DF分别交BC于点G、H,若AB = 3DG,则 =               13.如图.将矩形ABCD绕点A逆时针旋转90°至矩形AEFG点D的旋转路径为DG,若AB=1.BC=2,则阴影部分的面积为             (结果保留根号和π).14.如图，在RtSABC中.∠BAC = 90°,∠B= 45',AD是边BC上的中线，点E为边AC的中点点F为线段AD上的动点，连接FE FC.若AB = 2.则FE+FC的最小值为              三、解答题(每小题5分,共20分)15.先化简,再求值:a(a+4)+(2a-1)2 ,其中a=.    16.甲.乙、丙、丁四位同学进行一次乒兵球单打比赛.婴从中选出两位同卡打第一场比赛，(1)若已确定甲打第场，再从其余三 位同学中随机选取一位，则怡好选中乙同学的概率为   (2)请用画树状图或列表的方法,求恰好选中丙、T两位同学的概率。   17.为了让学生崇尚劳动，尊重劳动，在劳动中提升综合素质,某校定期开展劳动实践活动.甲、乙两班在一次体验摘草莓的活动中，甲班摘120千克草莓与乙班捎150千克草莓所用的时间相同.已知甲班平均每小时比乙班少摘10千克草称.求乙班平均每小时摘草莓的重量.    18.如图，ED⊥ABFC⊥AB ,垂足分别为D.C.AC= BD.AE = BF.求证:0AED≌△BFC. 四、解答题(每小题7分,共28分)19.图D.图②、图③均是6X6的正方形网格，每个小正方形的顶点称为格点,小正方形的边长均为1.点A.B.C均在格点上，只用无刻度的直尺在给定的网格中按要求画图。(1)在图①中，将△ABC沿射线AA'方向平移，当点八平移到点A'时，画出平移后的∆A'B'C';(2)在图②中，作△ABC关于直线DE成轴对称的△A1B1C1;(3)在图③中作△ABC关于点O成中心对称的△A2B2C2.   20.2022年4月到2023年4月我国原油进口月度走势图如图所示.根据图中信息解答下列问题.(1)2023年1-2月我国原油进口             万吨;(2)2022年4月到2022年12月我国原油进口当月增速的中位数是        %;(3)与2023年3月相比,2023年4月我国原油进口增加了          万吨;(4)观察我国原油进口月度走势图,2023年4月原油进口量比2022年4月增加267万吨，当月增速为6.6%(计算方法:2X100%≈6.6%).2023年3月当月增速为-14.0%，设2022年3月原油进口量为x万吨，下列算法正确的是          (填序号). ①x 100% =- 14.0%.②x 100%=- 14.0%.   21.在某海城开展的“海上联合”反潜演习中.我方军舰要到达C岛完成任务.已知军舰位干B市的南偏东25°方向上的A处，且在C岛的北偏东58°方向上.B市在C岛的北偏东28°方向上，且距离C岛372km.此时.我方军舰沿着AC方向以30km/h的速度航行，水我方军舰大约需要多长时间到达C岛(参考数据:≈1.73., sin53°≈,cos53°≈,tan53°≈).  22.如图,正比例函数y= 3x的图象与反比例函数y=(x> 0)的图象交于点C(2,c)，点A在x轴的正半轴上，四边形0ABC是平行四边形,y= (x> 0)的图象经过线段AB的中点M.(1)求c、k的值;(2)求平行四边形OABC的面积. 五、解答题（每小题8分，共16分）23.经村委会和政府部门同意，老王在自家门前建了一个简易温泉水供给站。某日老王刚刚给自家的存储罐注满温泉水拉温泉水的车队就来到了他家门前，当拉水的车辆（每辆车的型号都相同）依次停好后他打开出水阀给拉水车注入温泉水，经过2.5分钟第一辆拉水车装满温泉水离开（每辆拉水车之间的间隔时间忽略不计），当他给第二辆拉水车注满温泉水时，入水阀门自动打开为存储罐匀速注入温泉水并在他给第8辆车注满温泉水时，入水阀门恰似一江春水向东流好给存储罐加满温泉水后自动关闭。已知存储罐内温泉水量y(吨）与时间x(分钟）之间的部分函数图象如图所示：（1）a=            ,b=             c=            （2）当入水阀门自动打开为存储罐匀速注入温泉水到自动关闭时，求y与x之间的函数关系式。（3）当老王给第6辆拉水车注满温泉水时，求存储罐内剩余的温泉水量。    24. [感知]如图①,若AB = CD,AB // CD,易证AE = DE(不用证明);[探究]如图②,正方形ABCD和正方形CGEF的边BC、CF在同一条直线上,点G在CD上,AE、BD相交于点H,求证:AH = EH;[应用]如图③,在“探究”的条件下,连接CH,若BC=4,GE = 2,则CH =                        六、解答题(每小题10分，共20分)25.如图，在口ABCD中,BD⊥AB.∠A= 45°,AB = 2cm. 点P从点A出发，船折线AB—BC向终点C运动,点P在AB边、BC边上的运动速度分别为1cm/s，cm/s.在点P运动的过程中，过点P作直线AB的垂线,交折线AD— DC于点Q,以DQ为边向其下方作正方形DQMN.设点P的运动时间为t(s),正方形DQMN与▭ABCD重叠部分的面积为S(cm2).(1)点B、D之间的距离为           cm;(2)当点M落在边BC上时，求t的值;(3)当点P与点M重合前，求S与t之间的函数关系式。        26.如图，在平面直角坐标系中，抛物线y=x2-4x+c的顶点的纵坐标为- 2,A(m,y1)、B(m + t,y2)是抛物线上的两点,其中t> 0,记抛物线在点A、B之间的部分为图象G(包含A、B两点).(1)求抛物线对应的函数关系式;(2)当y1 = y2时,求m的取值范围;(3)若t=1,当图象G的最低点到x轴的距离等于抛物线的最低点到x轴的距离时，求m的取值范围;(4)当抛物线的顶点是图象G的最低点时,图象G.上最高点与最低点的纵坐标之差为3,求t的取值范围.        参考答案 一、1.A 2.B 3.C 4.A 5.B 6.D二、7.(a+2)(a-2) 8. 7.9m9.n< 10.4x+y=5y+x 内错角相等,两直线平行 13.+14.三、15.解:原式= 5a2+1.当a=时，原式= 36.16.解:(1)(2)画树状图如图。共有12种可能的情况,恰好选中丙、丁两位同学的情况有2种，所以恰好选中丙、丁两位同学的概率是17.解:设乙班平均每小时摘x千克草莓，由题意,得解得x = 50.经检验,x= 50是所列方程的解，且符合题意。答:乙班平均每小时摘50千克草莓. 证明:∵ED⊥AB,FC」AB,∴∠ADE=∠BCF =90°,∵AC= BD,∴AC +CD= BD+CD,即AD= BC.在Rt△ADE与Rt△BCF中，∴ Rt△ADE≊Rt△BCF(HL).四、19.解:(1)如围①所示，(2)如图②所示，(3)如图②所示，20.解:(1)8514.(2)- 11. 0.(3)32.(4)②.21.解:过点A作AD⊥BC于点D,由题意，得∠ACB= 58°- 28°= 30°,∠ABC=28°+25°= 53°,BC = 372km.设AD = xkm,在Rt△ABD中，∠ABD = 53°，∴ BD=x(km)，在Rt△ACD中，∵∠ACD = 30°,∴CD =x(km),∵BC= BD+CD,∴x+x= 372，解得x= 150，∴AC = 2AD = 300(km)，∵300÷30= 10(h),∴我方军舰大约需要10h到达C岛.22.解:(1)c= 6,k= 12.(2)平行四边形OABC的面积为18.五、23.解:(1)5;5;20.(2)当5≤x≤20时，设y= kx+n，代入点(5,5)、(20,25)，得 解 ∴ y=x-(5≤x≤20).(3)当x=2.5X6=15时,y=x15- =即存储罐内剩余的温泉水量24. [探究]证明:如图，延长EG交BD于点M,作MN⊥BC于点N,∴∠MNF = 90°，∵四边形CGEF是正方形，∴∠GEF =∠F= 90°,EF = CF.∴四边形EFNM是矩形，∴EM=FN,EF=MN.∵四边形ABCD是正方形，∴∠MBN=∠BMN = 45°，∴MN = BN,∴BN = CF.∴ME = FN = BC = AD.∵∠ADC=∠DGE = 90°，∴ME // AD，∴∠ADM= HME.∵∠AHD =∠MHE ,AD= ME,∴∆AHD≌△EHM,∴AH = EH.[应用]解:. 六、25.解:(1)2.(2)当点M与点B重合时，2t= 2，解得t=1;当点M与点P重合时,t-2= 1,解得t= 3.(3)当0<t≤1时,S=-t2+3;当1<t<2时,S= 2t2- 8t+8;当2< t < 3时,S= (t-2)2 =t2+4- 4t.26.解:(1)∵ 抛物线的顶点的纵坐标为一2,对称轴为直线x= 2,∴-2= 4-8+c,解得c= 2，∴抛物线对应的函数关系式为y=x2-4x+ 2.(2)∵抛物线的对称轴为直线x=2,且y1 = y2,t>0,∴m+t-2=2- m,解得t=- 2m+4,∵t> 0,∴-2m+4> 0，解得m < 2.(3)m的取值范围是m=-1或1≤m≤2或m= 4.(4)∵对称轴为直线x=2,顶点为(2,-2)，y的最小值是2,∵抛物线的顶点是图象G的最低点,∴ m≤2≤m+t. ∵最高点与最低点的纵坐标之差为3,∴抛物线的最高点的纵坐标为1,当y=1时,x2-4x+2= 1,解得x1=2-,x2 =2+当m=2-时，则2≤m+t≤2+,解得≤t≤2;当m+t=2+时，则2-≤m≤2,解得≤t≤2.综上所述，t的取值范围是≤t≤2.