高中数学上教版（2020）必修 第二册第8章 平面向量8.4 向量的应用课前预习课件ppt

这是一份高中数学上教版（2020）必修 第二册第8章 平面向量8.4 向量的应用课前预习课件ppt，共14页。PPT课件主要包含了４向量的应用，随堂检测等内容，欢迎下载使用。
　 例５ 如图８-４-４，平面上A、B、C三点的坐标分别是（2,3）、（2,0）、（1,1）．已知小明在点B 处休憩，有只小狗沿着AC所在直线来回跑动．问：其在什么位置时，离小明最近？
记 则
设D 是直线AC上随着小狗跑动而动态变化的点，则 可写成 的形式，λ是实数．问题转化为：确定λ的值，使向量
的模｜ ｜取到最小值，此时向量的终点D 即为小狗离小明最近的位置
如果D 为D０使得， , 即 ，那么向量 的模取到最小值．于是，λ要满足 ，即＝ 故
从而 最终推出D０的坐标是
因此，当其在点 时，离小明最近．
例６ 用向量方法证明：
证明 如图８-４-５，建立平面直角坐标系，并设A、B是单位圆上的任意两点，而角α与β都是顶点在原点O、始边为 x 轴正半轴的角，其终边分别落在AB与OB上．考虑向量
我们要求出 （的余弦）．注意到交换α与β不影响要证明的公式，可以假设从 旋转到 的最小正角就是 ．这
个角与角α－β有相同的始边与终边，于是
又由于｜ ＝｜ ｜＝１，我们得到
另一方面，用向量的坐标表示来计算数量积，我们有
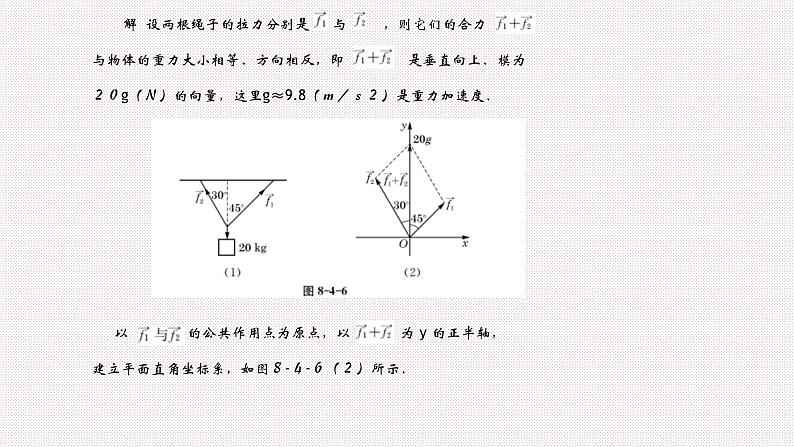
例７ 将质量为２０ｋｇ的物体用两根绳子悬挂起来，如图８-４-６(1)，两根绳子与铅垂线的夹角分别为４５°与３０°．求它们分别提供的拉力的大小．（结果精确到０．１Ｎ）
解 设两根绳子的拉力分别是 与 ，则它们的合力与物体的重力大小相等、方向相反，即 是垂直向上、模为２０g（Ｎ）的向量，这里g≈9.8（ｍ／ｓ２）是重力加速度．
以 的公共作用点为原点，以 为 y 的正半轴， 建立平面直角坐标系，如图８-４-６（２）所示．
令 则
因为 所以
解得 综上所述，这两根绳子所提供的拉力分别约为１０１．５Ｎ和１４３．５Ｎ．
1. 问题转化，即把物理问题转化为数学问题；
用向量方法解决物理学中的相关问题的步骤：
2. 建立模型，即建立以向量为载体的数学模型；
3. 求解参数，即求向量的模、夹角、数量积等；
4. 回答问题，即把所得的数学结论回归到物理问题中．
练习８．４（２） １．已知两个力（单位：： 的夹角为６０°，其中 （2.0）．某质点在这两个力的共同作用下，由点A（1，1）移动至点b（6，6）（单位：ｍ）． （１）求 ； （２）求 与 的合力对质点所做的功． ２．已知平面上三点A、B、C的坐标分别是（1,7）、（2,2）、（0,1），P为直线AC上的一动点．问：P在什么位置时， 取到最小值？
1. 一物体在力F的作用下，由点A(20, 15)移动到点B(7, 0). 已知F=(4, -5)，求F对该物体所做的功.
证明：如图, 在平面直角坐标系Oxy内作单位圆O, 以x轴的非负半轴为始边作角α, β, 它们的终边与单位圆O交点分别为A, B, 则