新教材适用2024版高考数学一轮总复习第7章立体几何第4讲空间直线平面的垂直课件

这是一份新教材适用2024版高考数学一轮总复习第7章立体几何第4讲空间直线平面的垂直课件，共60页。PPT课件主要包含了知识梳理·双基自测，名师讲坛·素养提升，考点突破·互动探究，②判定与性质，有且只有一条，垂线段的长度，任意一点到这个平面的，两个半平面，直二面角，ABD等内容，欢迎下载使用。
第四讲　空间直线、平面的垂直
知识梳理 · 双基自测
知识点一　直线与平面垂直(1)直线与平面垂直①定义：若直线l与平面α内的_________一条直线都垂直，则直线l与平面α垂直．
过一点垂直于已知平面的直线_____________________.过一点作垂直于已知平面的直线，则该点与垂足间的线段，叫做这个点到该平面的垂线段，_____________________叫做这个点到该平面的距离．一条直线与一个平面平行时，这条直线上____________________________，叫做这条直线到这个平面的距离．如果两个平面平行，那么其中一个平面内的任意一点到另一个平面的距离都相等，我们把它叫做这两个平行平面间的距离．
(2)直线与平面所成的角①定义：平面的一条斜线和它在平面上的射影所成的_________，叫做这条斜线和这个平面所成的角．若直线与平面平行或直线在平面内，直线与平面所成角为______，若直线与平面垂直，直线与平面所成角为_________.
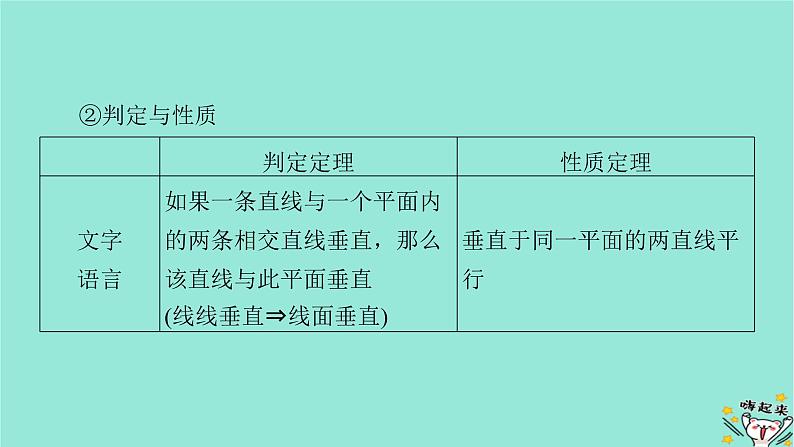
知识点二　平面与平面垂直(1)二面角的有关概念①二面角：从一条直线出发的__________________所组成的图形叫做二面角．②二面角的平面角：以二面角的棱上任意一点为端点，在两个半平面内分别作与棱_________的射线，则两射线所成的角叫做二面角的平面角．③二面角θ的范围：θ∈[0，π]．
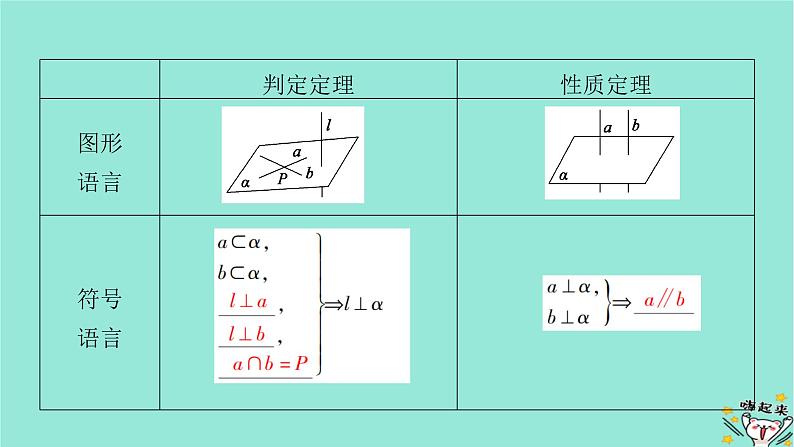
(2)平面与平面垂直①定义：两个平面相交，如果它们所成的二面角是____________，就说这两个平面互相垂直．②判定与性质
1．若两条平行线中的一条垂直于一个平面，则另一条也垂直于这个平面．2．若一条直线垂直于一个平面，则它垂直于这个平面内的任何一条直线(证明线线垂直的一个重要方法)．3．垂直于同一条直线的两个平面平行．4．一条直线垂直于两平行平面中的一个，则这条直线与另一个平面也垂直．
题组一　走出误区1．判断下列结论是否正确(请在括号中打“√”或“×”)(1)直线l与平面α内的无数条直线都垂直，则l⊥α.( 　　)(2)垂直于同一个平面的两平面平行．( 　　)(3)若直线a⊥α，b⊥α，则a∥b.( 　　)(4)若α⊥β，a⊥β，则a∥α.( 　　)(5)若直线a⊥平面α，直线b∥α，则直线a与b垂直．( 　　)(6)若平面α内的一条直线垂直于平面β内的无数条直线，则α⊥β.( 　　)
题组二　走进教材2．(必修2P164T15)(2022·广州中学教学研究会调研)如图1，正方形SG1G2G3中，E、F分别是G1G2、G2G3的中点，D是EF的中点，如图2，沿SE、SF、EF将正方形折成一个四面体，使G1、G2、G3重合，重合后的点记为G，则在四面体S－EGF中( 　　)A．SG⊥平面EFG B．SD⊥平面EFGC．GF⊥平面SEF D．GD⊥平面SEF
[解析]　由题意知SG⊥GF，SG⊥GE，GF∩GE＝G.∴SG⊥平面GEF，故选A.
题组三　走向高考4．(2019·北京)已知l，m是平面α外的两条不同直线．给出下列三个论断：①l⊥m；②m∥α；③l⊥α.以其中的两个论断作为条件，余下的一个论断作为结论，写出一个正确的命题：__________________________________________________.
若l⊥α，l⊥m，则m∥α.(或若l⊥α，m∥α，则l⊥m)
[解析]　由l，m是平面α外的两条不同直线，及线面平行的判定定理得：若l⊥α，l⊥m，则m∥α，若l⊥α，m∥α，则由线面垂直的性质和线面平行的性质得l⊥m，∴若l⊥α，m∥α，则l⊥m，故答案为：若l⊥α，l⊥m，则m∥α.(或若l⊥α，m∥α，则l⊥m)．
5．(2021·全国高考节选)已知直三棱柱ABC－A1B1C1中，侧面AA1B1B为正方形，AB＝BC＝2，E，F分别为AC和CC1的中点，BF⊥A1B1，D为棱A1B1上的点，证明：BF⊥DE.
[证明]　证法一：取BC的中点H，连EH、B1H，∵E为AC的中点，∴EH∥AB，又AB∥A1B1，∴EH∥A1B1，即E、H、B1、D共面，又A1B1⊥BF，∴EH⊥BF.又AB＝BC，由题意易知四边形BCC1B1为正方形，又F为CC1的中点，
∴BF⊥HB1，又HB1∩EH＝H，∴BF⊥平面EHB1D，又ED⊂平面EHB1D，∴BF⊥ED.证法二：由题意知AB⊥BB1.又BF⊥A1B1，AB∥A1B1，∴AB⊥BF，∴AB⊥平面BCC1B1.∴AB⊥BC.又AB＝BC＝2，E、F分别为AC、CC1的中点，
证法三：同证法二可知AB、BC、BB1两两垂直，如图建立空间直角坐标系，∵AB＝BC＝2，∴E(1,1,0)，B(0,0,0)，F(0,2,1)，D(a,0,2)(0≤a≤2)，
考点突破 · 互动探究
(1)(多选题)(2022·湖南名校联考)对于不同直线m，n和不同平面α，β，有如下四个命题，其中正确的是( )A．若m⊥α，n∥β，m⊥n，则α∥βB．若m⊥α，m∥n，n⊂β，则α⊥βC．若n⊥α，n⊥β，m⊥α，则m⊥βD．若m⊥α，m⊥n，则n∥α
(2)(2022·广东珠海模拟)已知α，β是两个不同的平面，l，m，n是三条不同的直线，下列条件中，可以得到l⊥α的是( 　　)A．l⊥m，l⊥n，m⊂α，n⊂αB．l⊥m，m∥αC．α⊥β，l∥βD．l∥m，m⊥α
[解析]　(1)选项A，若m⊥α，n∥β，m⊥n，则α与β可能相交可能平行，故A不正确；选项B，若m⊥α，m∥n，则n⊥α，又n⊂β，所以α⊥β，故B正确；选项C，若n⊥α，n⊥β，则α∥β，又m⊥α，所以m⊥β，故C正确；选项D，若m⊥α，m⊥n，则n∥α或n⊂α，故D不正确．故选BC.
(2)由α，β是两个不同的平面，l，m，n是三条不同的直线，知：对于A，l⊥m，l⊥n，m⊂α，n⊂α，则l与α相交、平行或l⊂α，故A错误；对于B，l⊥m，m∥α，则l与α相交、平行或l⊂α，故B错误；对于C，α⊥β，l∥β，则l与α相交、平行或l⊂α，故C错误；对于D，l∥m，m⊥α，则由线面垂直的判定定理得l⊥α，故D正确．故选D.
解决这类线、面位置关系判定的问题一般是利用正方体模型或画图分析解决，其实最好的办法是笔当线，纸、手掌当面动态演示．如知a∥α，可将笔看成a，桌面看成α，让笔平移、旋转，如知a⊥α，将笔看成a，让笔平移，很容易做出正确判定，事半功倍．
〔变式训练1〕(1)(多选题)(2022·江苏泰州调研)已知直线l与平面α相交于点P，则( )A．α内不存在直线与l平行B．α内有无数条直线与l垂直C．α内所有直线与l是异面直线D．至少存在一个过l且与α垂直的平面
(2)(2022·安徽马鞍山质检)设α，β，γ是互不重合的平面，m，n是互不重合的直线，给出下面四个命题：①若α⊥γ，β⊥γ，则α∥β；②若m⊥α，m⊥β，则α∥β；③若m∥α，n⊥α，则m∥n；④若α⊥β，α∩β＝m，n⊥m，则n⊥β.其中所有正确命题的序号是( 　　)A．①② B．② C．④ D．②③
[解析]　(1)α内的直线与l相交或异面，A对，C错；直线l与它在平面α内的射影m所确定的平面β与平面α垂直，D对；平面α内与射影m垂直的直线也与l垂直，显然这样的直线有无数条，B对．故选ABD.(2)对①，若α⊥γ，β⊥γ，则α∥β或α与β相交，故①错；对②，若m⊥α，m⊥β，则α∥β，②对；对③，若m∥α，n⊥α，则m⊥n，③错；对④，若α⊥β，α∩β＝m，n⊥m，则n不一定垂直β，④错，故选B.
角度1　线、面垂直的判定
证明：PA⊥平面PBC.
证法二：因为△ABC是底面圆O的内接正三角形，且AE为底面直径，所以AE⊥BC.因为DO(即PO)垂直于底面，BC在底面内，所以PO⊥BC.又因为PO⊂平面PAE，AE⊂平面PAE，PO∩AE＝O，所以BC⊥平面PAE.又因为PA⊂平面PAE，所以PA⊥BC.设AE∩BC＝F，则F为BC的中点，连接PF.
角度2　线、面垂直的性质 (2022·山东菏泽一模(节选))如图，圆柱的轴截面ABCD是正方形，点E在底面圆周上，AF⊥DE，F为垂足．求证：AF⊥DB.
[证明]　由题意可知DA⊥底面ABE，BE⊂底面ABE，故BE⊥DA，由AB为直径知BE⊥AE，又AE∩DA＝A，DA⊂平面AED，AE⊂平面AED，故BE⊥平面AED，由AF⊂平面AED得AF⊥BE，又AF⊥DE，BE∩DE＝E，BE，DE⊂平面BED，故AF⊥平面BED，又DB⊂平面BED，∴AF⊥DB.
角度3　直线与平面所成的角 (2022·江苏无锡高三期末)正方体ABCD－A1B1C1D1中，M是正方形ABCD的中心，则直线B1M与平面A1C1B所成角的正弦值为( 　　)
[解析]　解法一：连B1D1交A1C1于H，连BD，DB1，DB1∩BH＝O，BH∩B1M＝N，易证B1D⊥平面A1C1B.∴∠B1NO即为B1M与平面A1C1B所成的角，且B1O⊥ON.
∴∠B1NO即为B1M与平面A1C1B所成的角，且B1O⊥ON.设正方体棱长为1，
1．证明线线垂直的常用方法(1)利用特殊图形中的垂直关系．如：直径所对圆周角是直角；菱形对角线互相垂直；等腰三角形底边上的中线、顶角平分线垂直底边．等等．(2)若知某些线段长度，常利用勾股定理的逆定理．(3)利用直线与平面垂直的性质．(4)向量法：a⊥b⇔a·b＝0.
2．证明线面垂直的常用方法(1)线面垂直的判定定理：l⊥a，l⊥b，a⊂α，b⊂α，a∩b＝P⇒l⊥α.(2)面面垂直的性质定理：α⊥β，α∩β＝l，a⊂α，a⊥l⇒a⊥β.(3)性质：①a∥b，b⊥α⇒a⊥α；②α∥β，a⊥β⇒a⊥α.
3．求直线与平面所成角的方法(1)定义法：①作，在直线上选取恰当的点向平面引垂线，确定垂足的位置是关键；②证，证明所作的角为直线与平面所成的角；③求，通过解三角形，求角．
所以AD2＋BD2＝AB2，所以AD⊥BD，因为PD⊥平面ABCD，BD⊂平面ABCD，所以PD⊥BD，又PD∩AD＝D，所以BD⊥平面PAD，又因PA⊂平面PAD，所以BD⊥PA.
(2)解法一：连PE，又PD⊥底面ABCD，∴PD⊥AB.∴AB⊥平面PDE，∴平面PAB⊥平面PDE.∴∠DPE为PD与平面PAB所成的角．
(2022·黑龙江大庆市质检)在四棱锥P－ABCD中，平面PAD⊥平面ABCD，PA＝PD＝2，四边形ABCD是边长为2的菱形，∠DAB＝60°，E是AD的中点．(1)求证：BE⊥平面PAD；(2)求点E到平面PAB的距离．
[解析]　(1)证明：连接BD，在△PAD中，PA＝PD＝2，E是AD的中点，∴PE⊥AD，∵平面PAD⊥平面ABCD，平面PAD∩平面ABCD＝AD，∴PE⊥平面ABCD，∴PE⊥BE，
又∵四边形ABCD是边长为2的菱形，∠DAB＝60°，∴△ABD为等边三角形，∴BE⊥AD，又∵PE∩AD＝E，PE⊂平面PAD，AD⊂平面PAD，∴BE⊥平面PAD.
(1)判定面面垂直的方法①面面垂直的定义；②面面垂直的判定定理(a⊥β，a⊂α⇒α⊥β)．(一般在一个平面内找交线的垂线，证此线与另一面垂直．)(2)在已知面面垂直时，一般要用性质定理进行转化．在一个平面内作交线的垂线，转化为线面垂直，然后进一步转化为线线垂直．
(3) (4)求点到平面距离的方法①定义法——作出点到平面的垂线段(借助过点与已知平面垂直的平面)，求其长度即可．②体积法．
(2)(2022·山东济宁模拟节选)如图，四边形ABEF是矩形，平面ABC⊥平面ABEF，D为BC中点，AB＝AC.证明：平面ADF⊥平面BCF.
[解析]　(1)取AD的中点O，连接OC交BD于F点，连接EF，∵△PAD是等边三角形，∴PO⊥AD，　　 ∵OD∥BC，BC＝2OD，∴FC＝2OF.又∵平面PAD⊥平面ABCD，PO⊥AD，
(2)证明：因为AB＝AC，D为BC中点，所以AD⊥BC，因为四边形ABEF是矩形，所以FA⊥AB，因为平面ABC⊥平面ABEF，平面ABC∩平面ABEF＝AB，AF⊂平面ABEF，所以AF⊥平面ABC，因为BC⊂平面ABC，所以AF⊥BC，又AF，AD⊂平面ADF，AF∩AD＝A，所以BC⊥平面ADF，又BC⊂平面BCF，所以平面ADF⊥平面BCF.
名师讲坛 · 素养提升
(1)(多选题)(2022·四省八校下学期开学联考改编)已知正方体ABCD－A1B1C1D1的棱长为2，M为DD1的中点，N为底面ABCD内一动点，则下列命题正确的个数是( )
(2)(多选题)(2021·山东日照模拟)已知正方体ABCD－A1B1C1D1的棱长为4，M为DD1的中点，N为ABCD所在平面上一动点，则下列命题正确的是( )
对于C，因为BB1⊥平面ABCD，所以点N到直线BB1的距离为NB，即点N到点B的距离与到直线DC的距离相等，又B不在直线DC上，所以点N的轨迹为以B为焦点，直线DC为准线的抛物线，故选项C正确；对于D，以D为坐标原点，DA，DC，DD1为x轴，y轴，z轴建立空间直角坐标系如图所示，
1．立体几何中的动态问题，准确抓住“动”与“定”的关系是解决问题的关键．2．立体几何中轨迹问题的解法：(1)利用平行、垂直关系转化为面面交线，或把空间数量关系转化为某平面内的数量关系确定动点轨迹；(2)若动点与定点的连线与定直线所成角为定值，则动点形成圆锥侧面，可通过分析平面与圆锥母线及轴的位置关系确定动点在该平面内的轨迹．(3)建立直角坐标系，求得轨迹方程进行判断．
〔变式训练4〕(1)(2022·安徽蚌埠质检)平面α的一条斜线AP交平面α于P点，过定点A的直线l与AP垂直，且交平面α于M点，则M点的轨迹是( 　　)A．一条直线 B．一个圆C．两条平行直线 D．两个同心圆
[解析]　(1)由题意知M在过A且与PA垂直的平面β内，∴点M的轨迹为平面α与β的交线，故选A.