2023年黑龙江省大庆市五校联考中考数学模拟试卷（含解析）

这是一份2023年黑龙江省大庆市五校联考中考数学模拟试卷（含解析），共29页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2023年黑龙江省大庆市五校联考中考数学模拟试卷
学校:___________姓名：___________班级：___________考号：___________
第I卷（选择题）
一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）
1. 下列实数中小于0的数是(    )
A. |2023| B. −2023 C. 2023 D. 12023
2. ChatGPT是一种人工智能技术驱动的自然语言处理工具.Snapchat将推出基于ChatGPT的自有聊天机器人，最终目标让Snapchat的7.5亿月活跃用户都可以使用该机器人.其中7.5亿用科学记数法表示为(    )
A. 7.5×108 B. 75×108 C. 7.5×109 D. 0.75×109
3. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是(    )
A. B. C. D.
4. 某校从各年级随机抽取50名学生，每人进行10次投篮，投篮进球次数如表所示：
进球次数
0
1
2
3
4
5
6
7
8
9
10
人数
1
9
9
8
6
6
5
4
1
1
0
该投篮进球次数的中位数是(    )
A. 2 B. 3 C. 4 D. 5
5. 如图，一次函数y1=−2x+n与y2=x+m的图象交于点(1,3)，则关于x的不等式x+m1
B. x3
D. x0)有且只有一个公共点，则k的值为(    )

A. 23 B. 53 C. 25 5 D. 6 55
10. 如图，已知抛物线L：y=−tx2+2(1−t)x+4 (常数t>0)与x轴分别交于点M(−2,0)和点N，与y轴交于点P，PQ//x轴交抛物线L于点Q，作直线MP和OQ.甲、乙、丙三人的说法如下：
甲：若t=2，则点Q的坐标为(−1,4)．
乙：若MN=2PQ，则t的值有两个，且互为倒数．
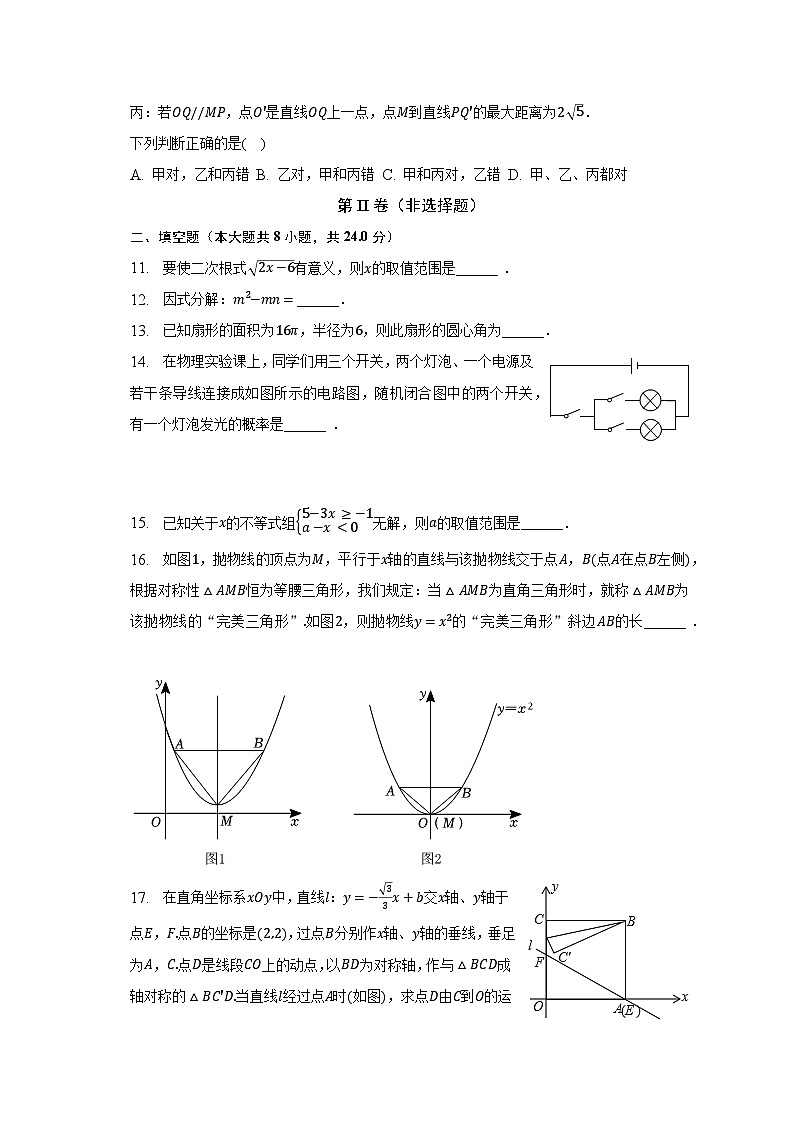
丙：若OQ//MP，点O′是直线OQ上一点，点M到直线PQ′的最大距离为2 5．
下列判断正确的是(    )
A. 甲对，乙和丙错 B. 乙对，甲和丙错 C. 甲和丙对，乙错 D. 甲、乙、丙都对
第II卷（非选择题）
二、填空题（本大题共8小题，共24.0分）
11. 要使二次根式 2x−6有意义，则x的取值范围是______ ．
12. 因式分解：m2−mn=______．
13. 已知扇形的面积为16π，半径为6，则此扇形的圆心角为______．
14. 在物理实验课上，同学们用三个开关，两个灯泡、一个电源及若干条导线连接成如图所示的电路图，随机闭合图中的两个开关，有一个灯泡发光的概率是______ ．


15. 已知关于x的不等式组5−3x≥−1a−x0交于点B1,m．

(1)求反比例函致的表达式；
(2)点M为反比例函数在第一象限图象上的一点，过点M作x轴垂线，交一次函数y=2x+b图象于点N，连接BM，若▵BMN是以MN为底边的等腰三角形，求▵BMN的面积；
(3)点P为反比例函数y=kxx>0图象上一点，连接PB，若∠PBA=∠BAO，求点P的坐标．

26. (本小题8.0分)
某校九年级学生小丽、小强和小红到某商场参加了社会实践活动，在活动中他们参与了某商品的销售工作，已知该商品的进价为40元/件，售价为60元/件，下面是他们在活动结束后的对话：小丽：我发现此商品如果按60元/件销售，每星期可卖出300件.小强：我发现在售价60元/件的基础上调整价格，每涨价1元，每星期比小丽所调查的销售量300件要少卖出10件.小红：我发现在售价60元/件的基础上调整价格，每降价1元，每星期比小丽所调查的销售量300件要多卖出20件．
(1)若设每件涨价x元，则每星期实际可卖出______ 件，每星期售出商品的利润y1(元)与x的关系式为y1= ______ ，x的取值范围是______ ；
(2)若设每件降价a元，则每星期售出商品的利润y2(元)与a的关系式为y2= ______ ；
(3)在涨价情况下，如何定价才能使每星期售出商品的利润最大？最大利润是多少？
27. (本小题8.0分)
如图，在Rt△ABC中，∠ACB=90°，D为AB边上的一点，以AD为直径的⊙O交BC于点E，交AC于点F，过点C作CG⊥AB交AB于点G，交AE于点H，过点E的弦EP交AB于点Q(EP不是直径)，点Q为弦EP的中点，连结BP，BP恰好为⊙O的切线．
(1)求证：BC是⊙O的切线．
(2)求证：EF=ED．
(3)若sin∠ABC═35，AC=15，求四边形CHQE的面积．

28. (本小题9.0分)
如图1，已知一次函数y=−x+3的图象与y轴，x轴相交于点A，B，抛物线y=−x2+bx+c与y轴交于点C，顶点M在直线AB上，设点M横坐标为m．

(1)如图2，当m=3时，求此时抛物线y=−x2+bx+c的函数表达式；
(2)求当m为何值时，点C的纵坐标最大；
(3)如图3，当m=0时，此时的抛物线y=−x2+bx+c与直线y=kx+2相交于D，E两点，连接AD，AE并延长，分别与x轴交于P，Q两点．试探究OP⋅OQ是否为定值？若是，请求出该定值；若不是，请说明理由．

答案和解析

1.【答案】B 
【解析】解：A.|2023|>0，故本选项不符合题意；
B.−20230，故本选项不符合题意；
D.12023>0，故本选项不符合题意．
故选：B．
先算绝对值，再根据实数的大小比较法则比较即可．
本题考查了实数的大小比较，算术平方根，绝对值等知识点，能熟记实数的大小比较法则是解此题的关键，注意：正数都大于0，负数都小于0，正数大于一切负数，两个负数比较大小，其绝对值大的反而小．

2.【答案】A 
【解析】解：7.5亿=750000000=7.5×108．
故选：A．
用科学记数法表示较大的数时，一般形式为a×10n，其中1≤|a|