数学（山西卷）-【试题猜想】2023年中考考前最后一卷（考试版+答题卡+全解全析+参考答案）

这是一份数学（山西卷）-【试题猜想】2023年中考考前最后一卷（考试版+答题卡+全解全析+参考答案），文件包含数学山西卷-试题猜想2023年中考考前最后一卷全解全析docx、数学山西卷-试题猜想2023年中考考前最后一卷参考答案docx、数学山西卷-试题猜想2023年中考考前最后一卷考试版A4docx、数学山西卷-试题猜想2023年中考考前最后一卷答题卡docx、数学山西卷-试题猜想2023年中考考前最后一卷考试版A3docx等5份试卷配套教学资源，其中试卷共47页， 欢迎下载使用。
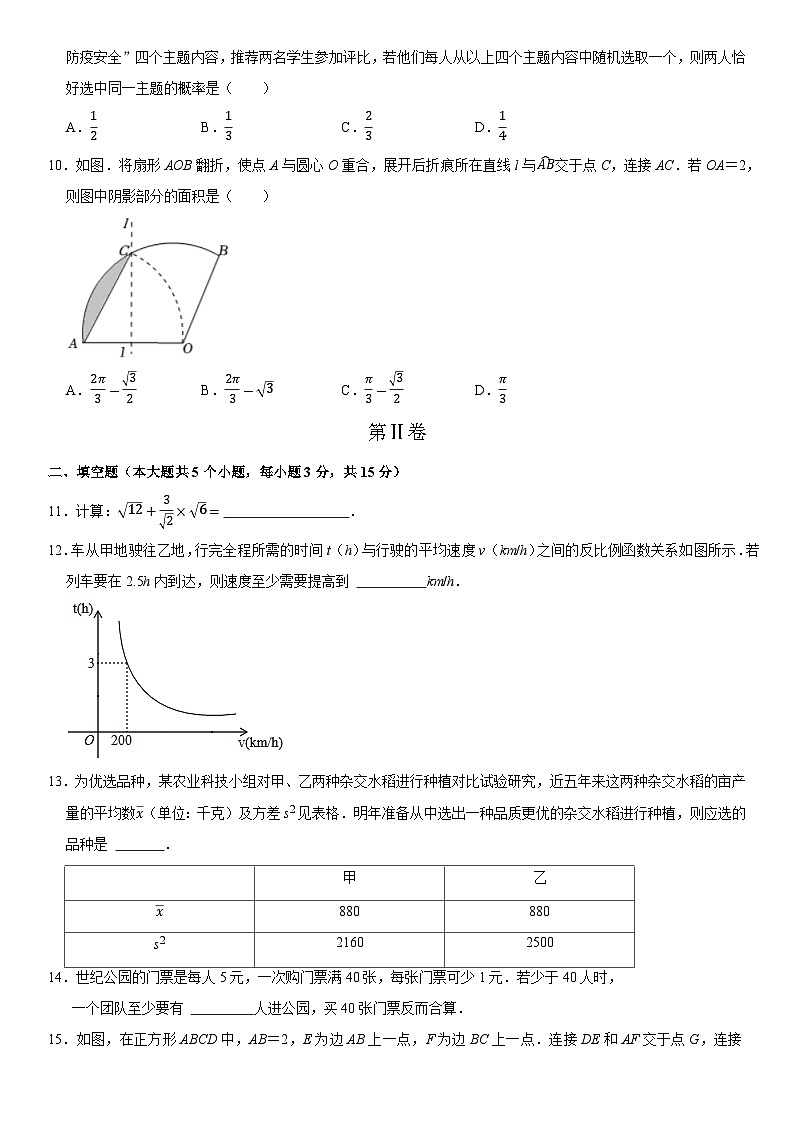
2023年中考考前最后一卷【山西卷】数学·参考答案 第Ⅰ卷一、选择题（本大题共10个小题，每小题3分，共30分。在每个小题给出的四个选项中，只有一项符合题目要求，请选出并在答题卡上将该项涂黑）12345678910BDBBABCADB1．解：15÷（﹣5）＝﹣3．答案：B．2．解：A．是轴对称图形，不是中心对称图形，故本选项不符合题意；B．不是轴对称图形，是中心对称图形，故本选项不符合题意；C．不是轴对称图形，是中心对称图形，故本选项不符合题意；D．既是轴对称图形，又是中心对称图形，故本选项符合题意．答案：D．3．解：28700+13100＝4.18×104．答案：B．4．解：3a﹣2a＝a，故选项A错误，不符合题意；a3•a5＝a8，故选项B正确，符合题意；a8÷2a2a6，故选项C错误，不符合题意；（3ab）2＝9a2b2，故选项D错误，不符合题意；答案：B．5．解：解不等式x﹣2≤0，得：x≤2，解不等式﹣x+1＞0，得：x＜1，则不等式组的解集为x＜1．答案：A．6．解：如图，根据题意可知∠A为直角，直尺的两条边平行，∴∠2＝∠ACB，∵∠ACB+∠ABC＝90°，∠ABC＝∠1，∴∠2＝90°﹣∠1＝90°﹣40°＝50°，答案：B．7．解：观察图形，横向距离大约是汽车的长度的2倍，∵汽车的长度大约为4米，∴横向距离大约是8米，由“跳眼法”的步骤可知，将横向距离乘以10，得到的值约为被测物体离观测点的距离值，∴汽车到观测点的距离约为80米，答案：C．8．解：∵∠A＝∠D，∠A＝48°，∴∠D＝48°，∵∠APD＝80°，∠APD＝∠B+∠D，∴∠B＝∠APD﹣∠D＝80°﹣48°＝32°，答案：A．9．解：设A，B，C，D分别代表交通安全、消防安全、饮食安全、防疫安全．画树状图如图：共有16种等可能的结果，两人恰好选中同一主题的结果有4种，则两人恰好选中同一主题的概率为．答案：D．10．解：连接CO，直线l与AO交于点D，如图所示，
∵扇形AOB中，OA＝2，∴OC＝OA＝2，∵点A与圆心O重合，∴AD＝OD＝1，CD⊥AO，∴OC＝AC，∴OA＝OC＝AC＝2，∴△OAC是等边三角形，∴∠COD＝60°，∵CD⊥OA，∴CD，∴阴影部分的面积为：，答案：B．第Ⅱ卷二、填空题（本大题共5个小题，每小题3分，共15分）11．解：原式＝235，答案：5．12．解：∵从甲地驶往乙地的路程为200×3＝600（km），∴汽车行驶完全程所需的时间t（h）与行驶的平均速度v（km/h）之间的关系式为t，当t＝2.5h时，即2.5，∴v＝240，答：列车要在2.5h内到达，则速度至少需要提高到240km/h．答案：240．13．解：因为甲、乙的平均数相同，又甲的方差比乙小，所以甲的产量比较稳定，则应选的品种是甲；答案：甲．14．解：设x人进公园，若购满40张票则需要：40×（5﹣1）＝40×4＝160（元），故5x＞160时，解得：x＞32，则当有32人时，购买32张票和40张票的价格相同，则再多1人时买40张票较合算；32+1＝33（人）．则至少要有33人去世纪公园，买40张票反而合算．答案：33．15．解：如图，取AD的中点T，连接BT，GT，
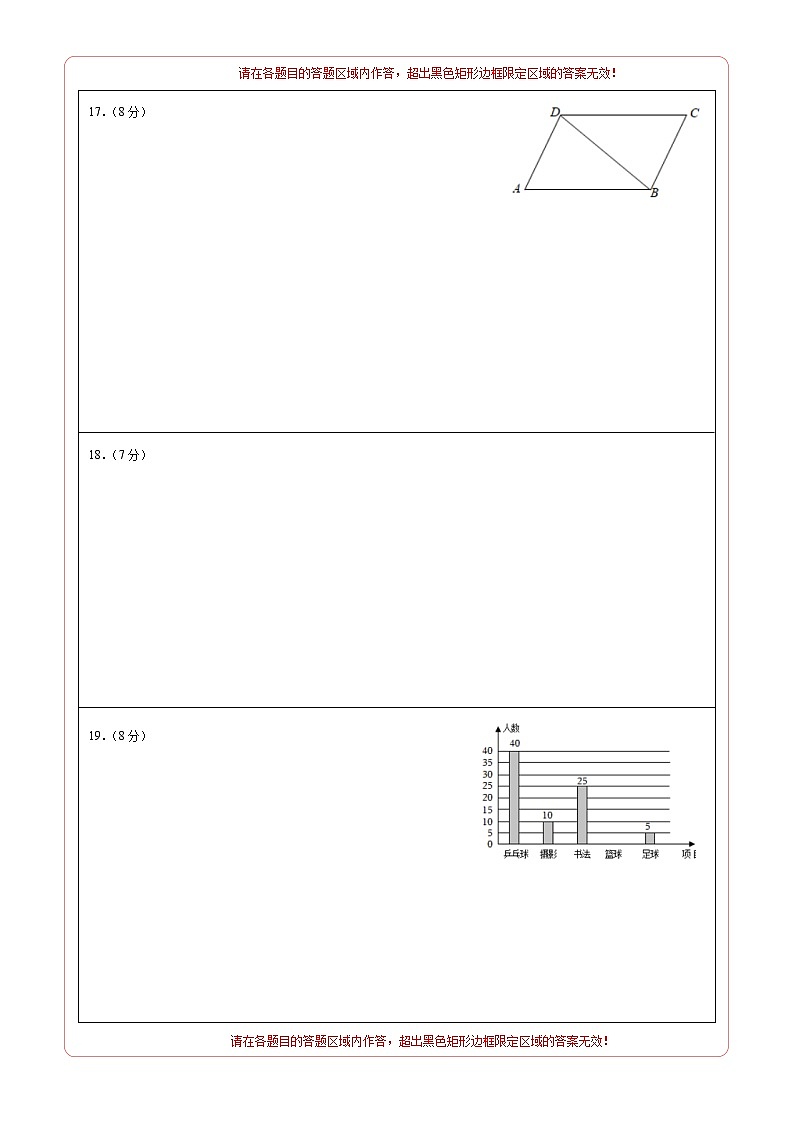
∵四边形ABCD是正方形，∴AD＝AB＝2，∠DAE＝∠ABF＝90°，在△DAE和△ABF中，，∴△DAE≌△ABF（SAS），∴∠ADE＝∠BAF，∵∠BAF+∠DAF＝90°，∴∠EDA+∠DAF＝90°，∴∠AGD＝90°，∵DT＝AT，∴GTAD＝1，BT，∴BG≥BT﹣GT，∴BG1，∴BG的最小值为1．答案：1．三、解答题（本大题共8个小题，共75分。解答应写出文字说明，证明过程或演算步骤）16．解：（1） ＝1；（2），②×2，得4x+2y＝﹣10③，①+③，得5x＝0，∴x＝0．把x＝0代入①，得y＝﹣5．∴所以原方程组的解为．17．解：（1）如图，EF、DE、BF为所作；（2）四边形DEBF为菱形．理由如下：如图，∵EF垂直平分BD，∴EB＝ED，FB＝FD，OB＝OD，∵四边形ABCD为平行四边形，∴CD∥AB，∴∠FDB＝∠EBD，在△ODF和△OBE中，，∴△ODF≌△OBE（ASA），∴DF＝BE，∴DE＝EB＝BF＝DF，∴四边形DEBF为菱形．18．解：设每个A型扫地机器人的进价为x元，则每个B型扫地机器人的进价为（2x﹣400）元，依题意得：，解得：x＝1600，经检验，x＝1600是原方程的解，且符合题意，∴2x﹣400＝2×1600﹣400＝2800．答：每个A型扫地机器人的进价为1600元，每个B型扫地机器人的进价为2800元．19．解：（1）根据乒乓球所占的比例和人数可得，抽取的人数为（人），∴参加篮球的人数有：100﹣40﹣10﹣25﹣5＝20（人），补全条形统计图如图所示：∵参加摄影的人数为10人，∴，∴m＝10；根据扇形图可得：1﹣40%﹣5%﹣25%﹣10%＝20%∴n＝20；（2）根据统计图可知“书法”所占25%，∴2000×25%＝500（人），∴若该校有2000名学生，估计该校参加“书法”活动的学生有500人；（3）根据条形统计图和扇形统计图可知，参加乒乓球的学生人数是最多的，其次是书法、篮球，参加摄影的学生人数相对来说是较少，最少的是参加足球的学生人数，所以可以适当的增加乒乓球这项课后服务活动项目的开设，减少足球课后服务活动项目的开设，以满足大部分同学的需求．20．解：（1）画出图象，根据图象可知，①当x≥0时，y随x的增大而增大，故错误；②该函数图象关于y轴不对称，故错误；③当x＝0时，函数有最小值为﹣1，正确；④该函数图象不经过第三象限，正确；答案：③④．（2）在平面直角坐标系xOy中画出该函数图象，①当x2﹣1＝8时，x＝3；当﹣x+1＝8时，x＝﹣7，∴若函数值y＝8，则x＝3或﹣7，答案：3或﹣7；②∵关于x的方程2x+c＝[x]有两个互不相等的实数根，∴可以看成是y＝[x]和y＝2x+c有两个交点．∵y＝2x+c是一次函数，与y轴的交点为C，∴当c＞1时，满足两个交点的条件．若将y＝2x+c向下平移与图象有两个交点，则c≤﹣1．∴方程为2x+c＝x2﹣1，即x2﹣2x﹣（1+c）＝0．∴Δ＝4+4（1+c）＞0，∴c＞﹣2，∴﹣2＜c≤﹣1．答案：c＞1或﹣2＜c≤﹣1．21．解：∵∠1＝∠FAO，∠2＝∠EBO，∠1+∠2＝90°，∴∠FAO+∠EBO＝90°，∵OF⊥OA，∴∠O＝90°，∴∠FAO+∠AFO＝90°，∴∠EBO＝∠AFO，∵∠O＝∠O，∴△EBO∽△AFO，∴，∵OE＝15米，OF＝21.6米，OA＝16米，∴，解得OB＝20.25，∴AB＝OB﹣OA＝20.25﹣16＝4.25（米），答：河宽AB为4.25米．22．解：（1）如图1，延长CE交AB于H，∵∠ABC＝45°，AD⊥BC，∴∠ADC＝∠ADB＝90°，∠ABC＝∠DAB＝45°，∵DE＝CD，∴∠DCE＝∠DEC＝∠AEH＝45°，∴∠BHC＝∠BAD+∠AEH＝90°，∴CE⊥AB；（2）在△BED旋转的过程中CE′与AB′的位置关系与（1）中的CE与AB的位置关系是一致，理由如下：如图2，延长CE'交AB'于H，由旋转可得：CD＝DE'，B'D＝AD，∵∠ADC＝∠ADB＝90°，∴∠CDE'＝∠ADB'，又∵1，∴△ADB'∽△CDE'，∴∠DAB'＝∠DCE'，∵∠DCE'+∠DGC＝90°，∴∠DAB'+∠AGH＝90°，∴∠AHC＝90°，∴CE'⊥AB'；（3）如图3，过点D作DH⊥AB'于点H，∵△BED绕点D顺时针旋转30°，∴∠BDB'＝30°，B'D＝BD＝AD，∴∠ADB'＝120°，∠DAB'＝∠AB'D＝30°，∵DH⊥AB'，∴AD＝2DH，AHDH＝B'H，∴AB'AD，由（2）可知：△ADB'∽△CDE'，∴∠DCE'＝∠DAB'＝30°，∵AD⊥BC，CD，∴DG＝1，CG＝2DG＝2，∴CG＝FG＝2，∵∠DAB'＝30°，CE'⊥AB'，∴AG＝2GF＝4，∴AD＝AG+DG＝4+1＝5，∴AB'AD＝5．23．解：（1）将点A（﹣1，0），B（5，0）代入y＝﹣x2+bx+c中，得，解这个方程组得，∴二次函数的表达式为y＝﹣x2+4x+5；（2）过点M作ME⊥x轴于点E，如图：设△BMN面积为S，根据题意得：ON＝t，BM．∵B（5，0），∴BN＝5﹣t，在y＝﹣x2+4x+5中，令x＝0得y＝5，∴C（0，5），∴OC＝OB＝5，∴∠OBC＝45°．∴ME＝BMsin45°，∴SBN•ME（5﹣t）•tt2t（t）2，∵0＜t＜5，∴当时，△BMN的面积最大，最大面积是；（3）存在点Q，使以A，C，P，Q为顶点的四边形是平行四边形，理由如下：由B（5，0），C（0，5）得直线BC解析式为y＝﹣x+5，设Q（m，﹣m+5），P（n，﹣n2+4n+5），又A（﹣1，0），C（0，5），①当PQ，AC是对角线，则PQ，AC的中点重合，∴，解得m＝0（与C重合，舍去）或m＝﹣7，∴Q（﹣7，12）；②当QA，PC为对角线，则QA，PC的中点重合，∴，解得m＝0（舍去）或m＝7，∴Q（7，﹣2）；③当QC，PA为对角线，则QC，PA的中点重合，∴，解得m＝1或m＝2，∴Q（1，4）或（2，3），综上所述，Q的坐标为（﹣7，12）或（7，﹣2）或（1，4）或（2，3）．