2022-2023学年江苏省淮安市淮安区五年级（下）期中数学试卷

这是一份2022-2023学年江苏省淮安市淮安区五年级（下）期中数学试卷，共13页。试卷主要包含了填空，选择，计算，解决问题等内容，欢迎下载使用。
2022-2023学年江苏省淮安市淮安区五年级（下）期中数学试卷
一、填空（每空1分，共22分）
1．（1分）今年小红a岁，妹妹（a﹣5）岁，5年后，她们相差 　 　岁。
2．（4分）若a、b都是大于0的自然数，且a÷b＝6，则a、b的最大公因数是 　 　，最小公倍数是 　 　；a和b是非0自然数，若a＝b+1，则a和b的公因数是 　 　，最小公倍数是 　 　。
3．（2分）如果3x＝0.18，那么x+1.56＝　 　，5x﹣3x＝　 　。
4．（5分）小华爸爸刚买了一辆新车，车牌号从左到右，第一位数是所有自然数（0除外）的公因数；第二位数既是偶数又是质数；第三位数是10以内最大的奇数；第四位数是最小的合数；第五位数的最大因数和最小倍数都是5。这个车牌号码是。
5．（3分）山阳小学乒乓球队买了4盒乒乓球，每盒10只，把这些乒乓球平均分给8个小组，每个小组分得盒，是 　 　只，每个小组分得的乒乓球占总数的。
6．（4分）3个相邻的自然数的和是45，其中最小的数是 　 　，最大的数是 　 　。这两个数的最大公因数是 　 　，最小公倍数是 　 　。
7．（1分）一个数既是60的因数，又是5的倍数，这个数最大是 　 　。
8．（2分）判断下列结果是奇数还是偶数。
（1）1×3×5×7……97×98×99×2的积是 　 　。
（2）15+16+17+18+……+36+37+38+39的和是 　 　。
二、选择（每题2分，共10分）
9．（2分）将数A分解质因数是A＝2×3×5，那么因数有（　　）个．
A．3 B．5 C．6 D．8
10．（2分）用10以内的3个不同的质数，组成是3和5的倍数的三位数，一共可以组成（　　）个这样的三位数。
A．1 B．2 C．3 D．4
11．（2分）把3块饼平均分给4个小朋友，每个小朋友能分到3块的（　　）
A． B． C．块 D．块
12．（2分）下列选项中，能用2a+6表示的是（　　）
A．整条线段的长度： B．整条线段的长度：
C．这个长方形的周长： D．这个图形的面积：
13．（2分）今年小明8岁，妈妈32岁，（　　）年后妈妈的年龄是小明的3倍。
A．2 B．4 C．6 D．8
三、计算（共26分）
14．（12分）解方程
4x+8＝60
（0.7+x）+0.2＝21
4x﹣0.6x＝17
1.6x+0.2×8＝8
15．（8分）求下面每组数的最大公因数和最小公倍数
26和13
11和13
16和12
15和40
16．（6分）看图列方程，并求出x的值

四、解决问题（42分，每题5分，第7题7分）
17．（5分）刘阿姨家种植黄瓜的面积比茄子的3倍少40平方米，比种植西红柿面积的1.5倍多50平方米。已知刘阿姨家种植黄瓜的面积是200平方米。（自己提出一个数学问题并列方程解答）
问题：　 　。
解题过程：　 　。
18．（5分）五（1）的同学在学习《蒜叶的生长》时，栽种了几行大蒜，每行的棵数一样多，四位同学一起数大蒜的棵数，只有一个人数对了，你知道是谁吗？你是怎样想的？请加以说明。
姓名
佳峰
宇阳
言丽
玉梁
棵数
41
43
45
47
19．（5分）王明过生日，妈妈买来16块小蛋糕和30块饼干平均分给王明和他的朋友们，结果小蛋糕少了2块，饼干多了3块。王明一共来了多少个朋友？
20．（5分）一辆客车和一辆货车从相距460千米的甲、乙两地出发，相向而行，2小时后相遇。已知客车每小时行驶120千米，求货车每小时行驶多少千米？
21．（5分）有4个小朋友，他们的年龄恰好是4个连续的自然数，他们的年龄的积是360，最大的小朋友多少岁？
22．（5分）“阳光明媚春三月，正是踏青好时节”，五（6）班同学在一次春游野餐时，每2人合用了1个饭碗，每3个人合用1个菜碗，每4个人合用1个汤碗，野餐共用了78个碗，你知道这次参加野餐的有多少人吗？
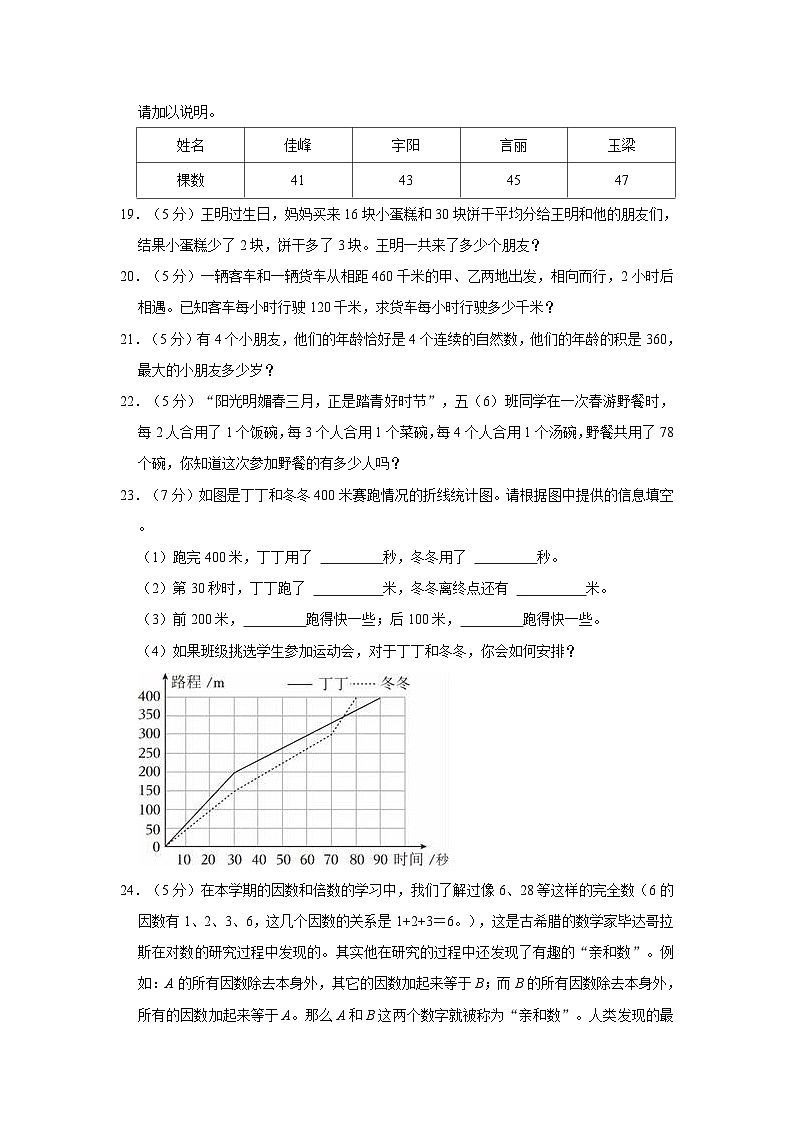
23．（7分）如图是丁丁和冬冬400米赛跑情况的折线统计图。请根据图中提供的信息填空。
（1）跑完400米，丁丁用了 　 　秒，冬冬用了 　 　秒。
（2）第30秒时，丁丁跑了 　 　米，冬冬离终点还有 　 　米。
（3）前200米，　 　跑得快一些；后100米，　 　跑得快一些。
（4）如果班级挑选学生参加运动会，对于丁丁和冬冬，你会如何安排？

24．（5分）在本学期的因数和倍数的学习中，我们了解过像6、28等这样的完全数（6的因数有1、2、3、6，这几个因数的关系是1+2+3＝6。），这是古希腊的数学家毕达哥拉斯在对数的研究过程中发现的。其实他在研究的过程中还发现了有趣的“亲和数”。例如：A的所有因数除去本身外，其它的因数加起来等于B；而B的所有因数除去本身外，所有的因数加起来等于A。那么A和B这两个数字就被称为“亲和数”。人类发现的最小的一对“亲和数”是220和 　 　。你知道横线上的数字是多少吗？请写出你的计算过程。

2022-2023学年江苏省淮安市淮安区五年级（下）期中数学试卷
参考答案与试题解析
一、填空（每空1分，共22分）
1．【分析】两个人之间年龄差始终不变，因此直接求出今年他们相差多少岁，即可求出过5年他们相差多少岁。
【解答】解：a﹣（a﹣5）
＝a﹣a+5
＝5（岁）
答：再过5年，她们相差5岁。
故答案为：5。
【点评】此题主要考查了两个人之间年龄差始终不变的知识点，要熟练掌握。
2．【分析】当两个数是倍数关系时，较小的数是它们的最大公因数，较大的数是它们的最小公倍数；当两个数是互质数时，最大公因数是1，最小公倍数是它们的乘积。据此解答。
【解答】解：若a、b都是大于0的自然数，且a÷b＝6，也就是a是b的倍数，则a、b的最大公因数是b，最小公倍数是a；
a和b是非0自然数，若a＝b+1，也就是a和b是互质数，则a和b的公因数是1，最小公倍数是ab。
故答案为：b，a，1，ab。
【点评】此题考查的目的是理解掌握求两个数的最大公因数、最小公倍数的方法及应用。
3．【分析】根据等式的性质，在方程3x＝0.18的左右两边同时除以3求得x的数值，进而把x的数值代入含字母的式子x+1.56和5x﹣3x中，再计算即可求得式子的数值。
【解答】解：3x＝0.18
3x÷3＝0.18÷3
x＝0.06
当x＝0.06时，
x+1.56
＝0.06+1.56
＝1.62
5x﹣3x
＝2x
＝2×0.06
＝0.12
故答案为：1.62，0.12。
【点评】此题考查了根据等式的性质解方程，也考查了含字母的式子求值的方法。
4．【分析】根据奇数和偶数，合数与质数的性质即可解答。
【解答】解：小华爸爸刚买了一辆新车，车牌号从左到右，第一位数是所有自然数（0除外）的公因数；第二位数既是偶数又是质数；第三位数是10以内最大的奇数；第四位数是最小的合数；第五位数的最大因数和最小倍数都是5。这个车牌号码是
【点评】此题考查了奇数和偶数，合数与质数的性质。
5．【分析】用盒数除以组数，求每组得到的盒数；用总只数除以组数，求每组得到的只数；用1除以组数，求每组得到的只数占总只数的几分之几。
【解答】解：4÷8＝
4×10÷8
＝40÷8
＝5（只）
1÷8＝
答：每个小组分得盒，是5只，每个小组分得的乒乓球占总数的。
故答案为：，5，。
【点评】本题主要考查分数的意义盒应用。
6．【分析】用3个相邻的自然数的和除以3，就是中间的自然数，再用中间的数减去1就是最小的自然数，用中间的数加上1就是最大的自然数；先把要求的两个数分别分解质因数，然后把它们公有的质因数连乘起来，所得的积就是它们的最大公因数，把它们公有的质因数和独有的质因数连乘起来，所得的积就是它们的最小公倍数。
【解答】解：45÷3＝15
最小：15﹣1＝14
最大：15+1＝16
14＝2×7
16＝2×2×2×2
所以这两个数的最大公因数是2，最小公倍数是2×2×2×2×7＝112。
故答案为：14，16，2，112。
【点评】本题主要考查了求两个数最大公因数和最小公倍数的方法，熟练掌握两个数公有的质因数连乘起来，所得的积就是它们的最大公因数，把它们公有的质因数和独有的质因数连乘起来，所得的积就是它们的最小公倍数是解题的关键。
7．【分析】根据因数、倍数的意义可知，一个数的因数的个数是有限的，最小的因数是1，最大的因数是它本身；一个数的倍数的个数是无限的，最小的倍数是它本身，没有最大倍数；据此解答即可。
【解答】解：60的最大因数是60，
5的倍数有：5、10、15、20、25、30、35、40......60；
所以一个数既是60的因数，又是5的倍数，这个数最大是60。
故答案为：60。
【点评】此题考查的目的是理解因数、倍数的意义，掌握求一个数的因数的方法、求一个数的倍数的方法及应用。
8．【分析】（1）无论1×3×5×7……97×98×99的积是奇数还是偶数，再和2相乘都是偶数，所以1×3×5×7……97×98×99×2的积是偶数；
（2）15到39有25个数，其中13个奇数和12个偶数，根据奇数+偶数＝奇数，加粗解答。
【解答】解：（1）1×3×5×7……97×98×99×2的积是偶数。
（2）15+16+17+18+……+36+37+38+39的和是奇数。
故答案为：偶数；奇数。
【点评】本题考查了奇数和偶数的性质。
二、选择（每题2分，共10分）
9．【分析】先求出A的乘积，再求这个数的约数，解决问题．
【解答】解：A＝2×3×5＝30，
30的自因数有：1、2、3、5、6、10、15、30，计8个．
答：A的因数有8个．
故选：D．
【点评】也可以这样解答：2、3、5各一次，还有2×3，2×5，3×5，2×3×5，再加上1，共8个．
10．【分析】10以内的质数有2，3，5，7，进而根据同时是3和5的倍数的特征是这个数个位上的数字是0或5，各个数位上的数字和是3的倍数，由此求解。
【解答】解：10以内的质数有2，3，5，7，
同时是3和5的倍数的三位数是：375和735。
答：一共可以组成2个这样的三位数。
故选：B。
【点评】本题主要考查同时是3、5的倍数的特征。
11．【分析】将3块饼看成单位“1”，平均分给4个小朋友，求每个小朋友能分到3块的几分之几，是求分率，平均分的是单位“1”，用单位“1”÷总份数即可。
【解答】解：由分析可得：每个小朋友能分到3块的1÷4＝。
故选：A。
【点评】解答此类问题要分清所求是分率还是具体的量，求分率平均分的是单位“1”，求具体的量，平均分的是总量。
12．【分析】A、整条线段的长度是a+2+6＝a+8，不符合题意；
B、整条线段的长度是a+6+6＝a+12，不符合题意；
C、长方形的周长是（a+3）×2＝2a+6，符合题意；
D、这个图形的面积是2a+6a＝8a，不符合题意．
据此解答即可．
【解答】解：长方形的周长是（a+3）×2＝2a+6，符合题意；
故选：C．
【点评】解答此题的关键是明确用字母表示数并计算长度、面积的方法．
13．【分析】设x年后妈妈的年龄是小明的年龄的3倍，那么这时小明的年龄就是（8+x）岁，妈妈的年龄是（32+x）岁，用小刚的年龄乘上3就是妈妈的年龄，由此列出方程求解．
【解答】解：设x年后妈妈的年龄是小刚的年龄的3倍，由题意得：
（8+x）×3＝32+x
24+3x＝32+x
2x＝8
x＝4
答：4年后妈妈的年龄正好是小刚的3倍。
故选：B。
【点评】解决本题设出未知数，表示出小刚和妈妈的年龄，再根据倍数关系列出方程求解。
三、计算（共26分）
14．【分析】（1）首先根据等式的性质，两边同时减去8，然后两边同时除以4即可；
（2）首先根据等式的性质，两边同时减去0.2，然后两边同时减去0.7即可；
（3）首先化简，然后根据等式的性质，两边同时除以3.4即可；
（4）首先根据等式的性质，两边同时减去1.6，然后两边再同时除以1.6即可。
【解答】解：（1）4x+8＝60
4x+8﹣8＝60﹣8
4x＝52
4x÷4＝52÷4
x＝13

（2）（0.7+x）+0.2＝21
0.7+x＝21﹣0.2
0.7+x＝20.8
0.7+x﹣0.7＝20.8﹣0.7
x＝20.1

（3）4x﹣0.6x＝17
3.4x＝17
3.4x÷3.4＝17÷3.4
x＝5

（4）1.6x+0.2×8＝8
1.6x+1.6＝8
1.6x+1.6﹣1.6＝8﹣1.6
1.6x＝6.4
1.6x÷1.6＝6.4÷1.6
x＝4
【点评】此题主要考查了根据等式的性质解方程的能力，即等式两边同时加上或同时减去、同时乘或同时除以一个数（0除外），两边仍相等。
15．【分析】求最大公因数也就是这几个数的公有质因数的连乘积，最小公倍数是公有质因数与独有质因数的连乘积求解；通常可先把每个分数中的分子分母分解质因数，再把它们公有的质因数相乘，有倍数关系的两个数的最大公因数是两个数中较小的那个数，最小公倍数是较大的数；如果两个数是互质数，它们的最大公因数是1，最小公倍数是它们的乘积，由此解决问题即可。
【解答】解：26和13 是倍数关系，最大公约数是13，最小公倍数是26；
13和11是互质数，最大公约数是1，最小公倍数是13×11＝143；
16和12，16＝2×2×2×2，12＝2×2×3；
最大公约数是2×2＝4，最小公倍数是2×2×3×2×2＝48；
15和40，15＝3×5，40＝2×2×2×5；
最大公约数是5，最小公倍数是2×2×2×3×5＝120。
故答案为：（1）13，26；（2）1，143；（3）4，48；（4）5，120。
【点评】此题主要考查求两个数的最大公因数的方法：两个数的公有质因数连乘积是最大公因数，有倍数关系的两个数的最大公因数是两个数中较小的那个数，如果两个数是互质数，它们的最大公因数是1；数字大的可以用短除解答。
16．【分析】根据等量关系：平行四边形的面积＝底×高，列方程解答即可。
根据等量关系：鸡的只数+鸭的只数＝55只，列方程解答即可。
【解答】解：27.2x＝108.8
x＝4
答：x为4。
x+3x+7＝55
4x+7＝55
4x＝48
x＝12
答：鸡有12只。
【点评】本题主要考查了列方程解应用题，关键是找等量关系。
四、解决问题（42分，每题5分，第7题7分）
17．【分析】刘阿姨家种植茄子多少平方米？（答案不唯一）设刘阿姨家种植茄子x平方米，根据等量关系：种植茄子的面积×3﹣40平方米＝种植黄瓜的面积，列方程解答即可。
【解答】解：刘阿姨家种植茄子多少平方米？（答案不唯一）
设刘阿姨家种植茄子x平方米。
3x﹣40＝200
3x＝240
x＝80
答：刘阿姨家种植茄子80平方米。
故答案为：刘阿姨家种植茄子多少平方米？（答案不唯一）
设刘阿姨家种植茄子x平方米。
3x﹣40＝200
3x＝240
x＝80
答：刘阿姨家种植茄子80平方米。
【点评】本题主要考查了列方程解应用题，关键是找等量关系。
18．【分析】因为大蒜的行数最少是两行，行数×棵数＝大蒜的数量，由此可知，大蒜的数量是合数，不是质数，据此判断。
【解答】解：因为41、43、47都是质数，所以佳峰、宇阳、玉梁都数错了；
45是合数，45＝5×9＝3×15，所以言丽数对了。
【点评】明确大蒜的棵数是合数是解题的关键。
19．【分析】根据妈妈买来16块小蛋糕和30块饼干平均分给王明和他的朋友们，结果小蛋糕少了2块，饼干多了3块，可知这些小朋友的人数是（16+2）、（30﹣3）的公因数，求出最大公因数，即可求出王明一共来了多少个朋友。
【解答】解：16+2＝18
30﹣3＝27
18＝2×3×3
27＝3×3×3
最大公因数是3×3＝9。
答：王明一共来了9个朋友。
【点评】解答此题的关键是根据题意判断出这些小朋友的人数是（16+2）、（30﹣3）的公因数。
20．【分析】相遇时两车行的路程和就是两地之间的距离，根据相遇问题的数量关系式：速度和×相遇时间＝路程，列方程解答。
【解答】解：设货车每小时行驶x千米。
（120+x）×2＝460
（120+x）×2÷2＝460÷2
120+x＝230
120+x﹣120＝230﹣120
x＝110
答：客车每小时行驶110千米。
【点评】本题考查列方程解应用题，解题关键是找出题目中的等量关系：速度和×相遇时间＝路程，列方程解答。
21．【分析】解答本题时首先把360分解质因数，然后把这些质因数转化为4个相邻的自然数。
【解答】解：根据分析可得：
360＝2×2×2×3×3×5＝3×（2×2）×5×（2×3）＝3×4×5×6
所以这四个小朋友的年龄分别是3岁、4岁、5岁、6岁。6最大。
答：最大的小朋友6岁。
【点评】本题是一道分解质因数类型的题目，解决这类问题的关键是明确相邻自然数相差1；分解质因数就是把一个合数分解成几个质因数的乘积的形式。
22．【分析】每2人合用一只饭碗，那么每个人用到饭碗的数量是，三人合用一只菜碗，那么每人用到菜碗的数量是个，四人合用一只汤碗，每人用到汤碗的数量是个，那么每个人用到了（++）个碗，用碗的总数除以每个人用到碗的数量就是参加野餐的人数。
【解答】解：78÷（++）
＝78÷
＝72（人）
答：这次参加野餐的有72人。
【点评】分数除法意义是解答本题的依据，关键是求出每个人用碗个数。
23．【分析】（1）通过观察统计图可知，实线表示丁丁用的时间，虚线表示冬冬用的时间，跑完400米，丁丁用了90秒，冬冬用了80秒。
（2）第30秒时，丁丁跑了200米，冬冬跑了150米，根据减法的意义，用减法求出冬冬离终点还有多少米。
（3）通过观察统计图可知，前200米，丁丁跑得快一些，后100米，冬冬跑得快一些。
（4）如果班级挑选学生参加运动会，我会选冬冬参加，因为冬冬有爆发力。据此解答。
【解答】解：（1）跑完400米，丁丁用了90秒，冬冬用了80秒。
（2）400﹣150＝250（米）
答：第30秒时，丁丁跑了200米，冬冬离终点还有250米。
（3）前200米，丁丁跑得快一些，后100米，冬冬跑得快一些。
（4）如果班级挑选学生参加运动会，我会选冬冬参加，因为冬冬有爆发力。
故答案为：90，80；200，250；丁丁，冬冬。
【点评】此题考查的目的是理解掌握复式折线统计图的特点及作用，并且能够根据统计图提供的信息，解决有关的实际问题。
24．【分析】根据“亲和数”的意义，先找出220的所有因数，再将除了它本身以外的其他因数相加，即可解答。
【解答】解：220的因数有：1、2、4、5、10、11、20、22、44、55、110、220
1+2+4+5+10+11+20+22+44+55+110
＝12+41+66+165
＝284
答：最小的一对”亲和数“是220和284。
故答案为：284。
【点评】解答本题需准确理解”亲和数“的意义和计算方法。