期末专题01 三角函数5.4-5.7小题综合-【备战期末必刷真题】高一下学期期末考试真题必刷满分训练（新高考湖南专用）

这是一份期末专题01 三角函数5.4-5.7小题综合-【备战期末必刷真题】高一下学期期末考试真题必刷满分训练（新高考湖南专用），文件包含期末专题01三角函数54-57小题综合-备战期末必刷真题高一下学期期末考试真题必刷满分训练新高考湖南专用解析版docx、期末专题01三角函数54-57小题综合-备战期末必刷真题高一下学期期末考试真题必刷满分训练新高考湖南专用原卷版docx等2份试卷配套教学资源，其中试卷共54页， 欢迎下载使用。
期末专题01 三角函数5.4-5.7小题综合

一、单选题
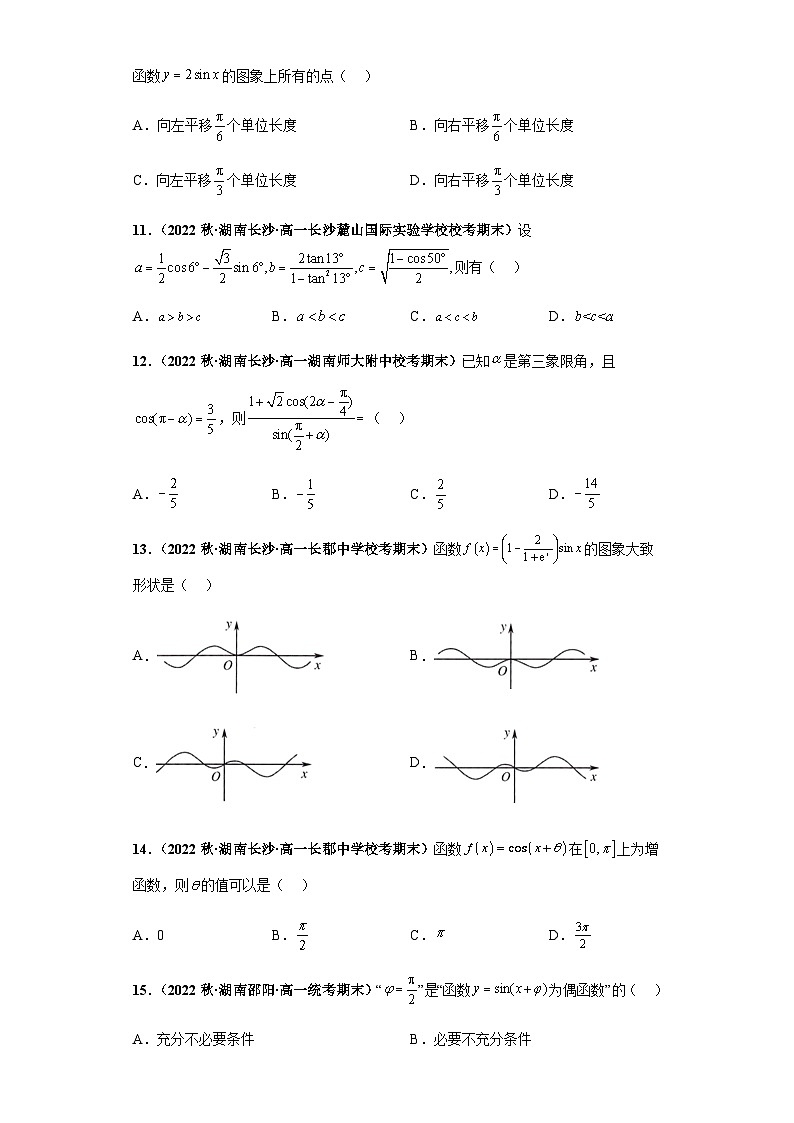
1．（2022秋·湖南长沙·高一湖南师大附中校考期末）（    ）．
A． B． C． D．
【答案】A
【分析】利用正弦的二倍角公式直接计算
【详解】，
故选：A
2．（2022秋·湖南益阳·高一统考期末）的值是（    ）
A． B． C． D．
【答案】B
【分析】利用两角差的正弦公式计算可得结果.
【详解】.
故选：B.
3．（2022秋·湖南娄底·高一统考期末）的值为（    ）
A． B． C． D．
【答案】C
【分析】利用两角差的正切公式化简可得结果.
【详解】.
故选：C.
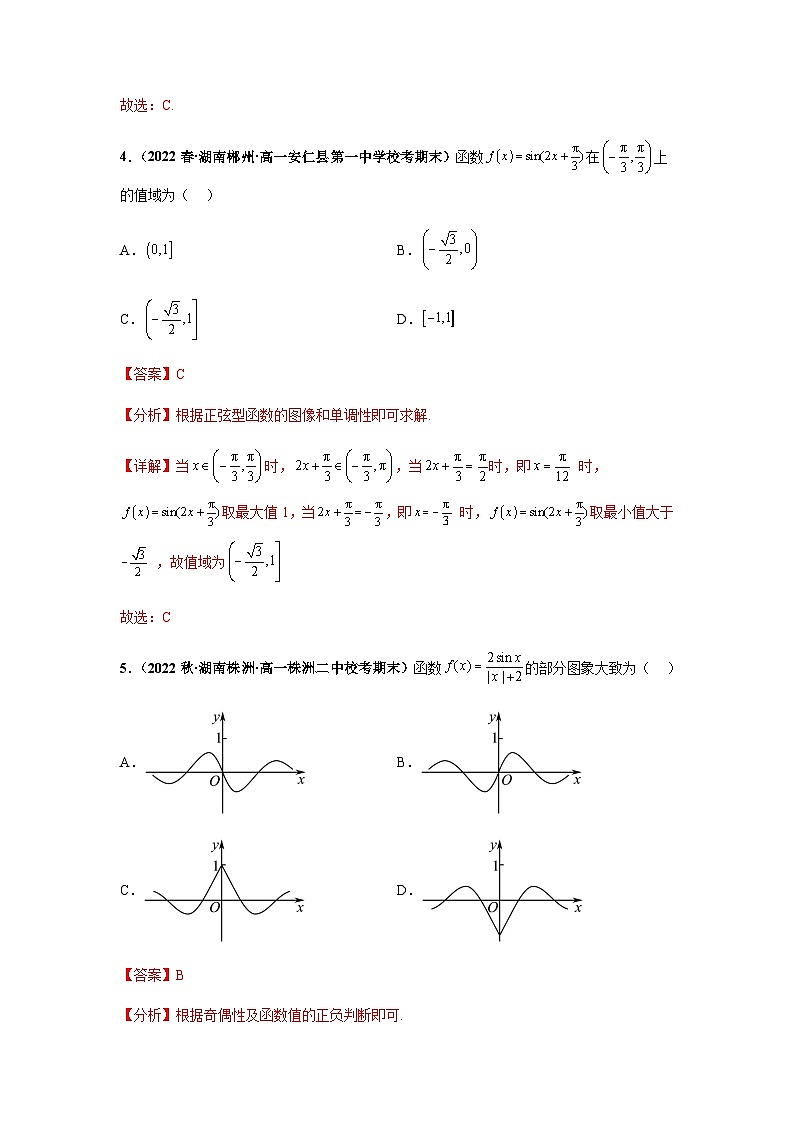
4．（2022春·湖南郴州·高一安仁县第一中学校考期末）函数在上的值域为（    ）
A． B．
C． D．
【答案】C
【分析】根据正弦型函数的图像和单调性即可求解.
【详解】当时，，当时，即 时，取最大值1，当，即 时，取最小值大于 ，故值域为
故选：C
5．（2022秋·湖南株洲·高一株洲二中校考期末）函数的部分图象大致为（    ）
A． B．
C． D．
【答案】B
【分析】根据奇偶性及函数值的正负判断即可.
【详解】因为，定义域为R
所以
所以为奇函数，且，排除CD
当时，，即，排除A
故选：B.
6．（2022秋·湖南岳阳·高一统考期末）将函数的图象上各点的横坐标伸长为原来的3倍，纵坐标保持不变，再将所得图象向右平移个单位，得到函数的图象，则的一个对称中心是（    ）
A． B． C． D．
【答案】B
【分析】先根据图象变换，求出变换后的函数解析式，然后根据解析式求解中心.
【详解】函数的图象上各点的横坐标伸长到原来的3倍得到图象的解析式为：，再向右平移个单位得到图象的解析式
当时，，所以是函数的一个对称中心.
故选：B.
7．（2022春·湖南郴州·高一安仁县第一中学校考期末）“”是“函数的最小正周期为”的（    ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
【答案】A
【分析】函数的最小正周期为，得，所以，结合充分必要条件理解判断．
【详解】由得，其最小正周期为，所以充分性成立；
但函数的最小正周期为，得，所以，必要性不成立.
所以“”是“函数的最小正周期为”的充分不必要条件.
故选：A．
8．（2022秋·湖南衡阳·高一统考期末）要得到函数的图象，只需将函数的图象上所有点的（    ）
A．横坐标伸长到原来的3倍，纵坐标不变，再向右平移个单位长度
B．横坐标伸长到原来的3倍，纵坐标不变，再向右平移个单位长度
C．横坐标缩短到原来的，纵坐标不变，耳向右平移个单位长度
D．横坐标缩短到原来的，纵坐标不变，再向右平移个单位长度
【答案】D
【分析】根据三角函数的图象变换，准确化简，即可求解.
【详解】先将的图象上所有点的横坐标缩短到原来的，纵坐标不变，可得，
再将向右平移个单位长度后，即可得到函数的图象．
故选：D.
9．（2022春·湖南·高一校联考期末）若，则（    ）
A． B． C． D．
【答案】A
【分析】利用二倍角公式计算可得；
【详解】解：因为，
所以.
故选：A.
10．（2022秋·湖南益阳·高一统考期末）为了得到函数的图象，只需把函数的图象上所有的点（    ）
A．向左平移个单位长度 B．向右平移个单位长度
C．向左平移个单位长度 D．向右平移个单位长度
【答案】C
【分析】利用三角函数图象变换可得结论.
【详解】为了得到函数的图象，只需把函数的图象上所有的点向左平移个单位长度.
故选：C.
11．（2022秋·湖南长沙·高一长沙麓山国际实验学校校考期末）设则有（    ）
A． B． C． D．
【答案】C
【分析】利用二倍角公式及两角差的正弦公式化简，再根据正弦函数的性质判断即可.
【详解】解：，
，
，
因为在上单调递增，
所以，
所以.
故选：C
12．（2022秋·湖南长沙·高一湖南师大附中校考期末）已知是第三象限角，且，则（    ）
A． B． C． D．
【答案】D
【分析】根据诱导公式及同角三角函数关系与二倍角公式即可得解.
【详解】由已知得，，则原式
.
故选：D
13．（2022秋·湖南长沙·高一长郡中学校考期末）函数的图象大致形状是（    ）
A． B．
C． D．
【答案】A
【分析】根据函数的奇偶性可得函数为偶函数，可排除CD，然后根据时的函数值可排除B.
【详解】因为，定义域为R，
又，
所以是偶函数，图象关于轴对称，故排除CD，
又当时，，，故排除B.
故选：A.
14．（2022秋·湖南长沙·高一长郡中学校考期末）函数在上为增函数，则的值可以是（    ）
A．0 B． C． D．
【答案】C
【分析】将选项代入分别验证单调性即可求解
【详解】对A, ,由余弦函数的性质可知在上为减函数，舍去；
对B，，在上先减后增，舍去
对C,，由余弦函数的性质可知在上为增函数.成立；
对D, ,在上先增后减，舍去
故选：C．
【点睛】本题通过三角函数的图象与性质，熟记单调性是关键，考查了学生的直观想象．
15．（2022秋·湖南邵阳·高一统考期末）“”是“函数为偶函数”的（    ）
A．充分不必要条件 B．必要不充分条件
C．充分必要条件 D．既不充分也不必要条件
【答案】A
【解析】根据充分必要条件的定义判断．
【详解】时，是偶函数，充分性满足，
但时，也是偶函数，必要性不满足．
应是充分不必要条件．
故选：A．
16．（2022秋·湖南株洲·高一株洲二中校考期末）下列函数中，以为最小正周期且在区间上单调递减的是（    ）
A． B． C． D．
【答案】B
【分析】根据三角函数的最小正周期、单调性对选项进行分析，从而确定正确选项.
【详解】A选项，对于函数，由得，
所以不满足“区间上单调递减”，A选项错误.
B选项，对于函数，根据函数的图象可知，函数的最小正周期为，
且函数在区间上单调递减，符合题意，B选项正确.

C选项，对于函数，其在区间上单调递增，不符合题意，C选项错误.
D选项，对于函数，最小正周期，不符合题意，D选项错误.
故选：B
17．（2022秋·湖南·高一校联考期末）若函数与函数都在区间上单调递增，则的最大值是（    ）
A． B． C． D．
【答案】A
【分析】首先求出函数的单调递增区间与函数的单调递增区间的交集，再与区间进行联系即可解决.
【详解】由，解得，
则的单调递增区间为．
由，解得，
则的单调递增区间为，
则，故．
故选：A
18．（2022秋·湖南湘潭·高一湘潭一中校联考期末）若函数（）在有最大值无最小值，则的取值范围是（    ）
A． B． C． D．
【答案】B
【分析】求出，根据题意结合正弦函数图象可得答案.
【详解】∵，∴，
根据题意结合正弦函数图象可得
，解得.
故选：B.
19．（2022秋·湖南长沙·高一长沙市明德中学校联考期末）已知函数（且），则的所有零点之和为（    ）
A． B． C． D．2
【答案】C
【分析】将的零点问题转化为函数和的图象的交点问题，因此可作出二者的图象，则问题可解.
【详解】因为，所以由，得，
因为函数与的图象都关于直线对称，
且与的图象在和时，各有2个交点，
如图示：

所以（且）的所有零点之和为,
故选：C．
20．（2022秋·湖南邵阳·高一统考期末）函数的图象大致是（    ）
A． B．
C． D．
【答案】A
【分析】根据奇偶性和的符号，使用排除法可得.
【详解】的定义域为R，
因为
，所以为偶函数，故CD错误；
又因为，，所以，故B错误.
故选：A
21．（2022秋·湖南衡阳·高一统考期末）若，则（    ）
A． B． C． D．
【答案】B
【分析】由同角三角函数的商数、平方关系，将条件化为，再根据二倍角余弦公式求目标式的值.
【详解】由题设，，
又.
故选：B.
22．（2022秋·湖南邵阳·高一统考期末）设直线与函数、、的图象在内交点的横坐标依次是、、，则（    ）
A． B． C． D．
【答案】A
【分析】根据直线与函数，，的图像在内交点的横坐标依次为，，，得到，再利用两角和的三角函数的公式求解.
【详解】因为直线与函数，，的图像在内交点的横坐标依次为，，，
所以，
所以，
所以，
所以.
故选：A.
23．（2022秋·湖南长沙·高一长郡中学校考期末）已知函数在内恰有3个最值点和4个零点，则实数的取值范围是（    ）
A． B． C． D．
【答案】B
【分析】数形结合，由第4个正零点小于等于1，第4个正最值点大于1可解.
【详解】，
因为，所以，
又因为函数在内恰有个最值点和4个零点，
由图像得：，解得：，
所以实数的取值范围是.

故选：B
24．（2022秋·湖南岳阳·高一统考期末）已知，则的值为（    ）
A． B． C．0 D．
【答案】B
【分析】利用诱导公式及同角三角函数的基本关系求出，再由二倍角公式及同角三角函数的基本关系将弦化切，最后代入计算可得.
【详解】解：因为，所以，所以，
所以

.
故选：B
25．（2022秋·湖南邵阳·高一统考期末）如图是函数在一个周期内的图象，则其解析式是（    ）

A． B．
C． D．
【答案】D
【解析】通过函数的图象可得到：A=3，，，则，然后再利用点在图象上求解.
【详解】由函数的图象可知：A=3，，，
所以，
又点在图象上，所以，
即，所以，
即，因为，，
所以，所以
故选：D.
【点睛】本题主要考查利用三角函数的图象求解析式，关键点是由图象观察出A=3，，再代入特殊点求，也就是找到振幅、周期、和初相，还考查了识图、运算求解的能力，属于中档题.
26．（2022秋·湖南邵阳·高一统考期末）已知函数，若互不相等，且，则的取值范围是（    ）
A． B． C． D．
【答案】D
【分析】结合对称性求得的取值范围.
【详解】依题意，
，关于对称.
不妨设，
则，
，
所以，
即.
故选：D

二、多选题
27．（2022秋·湖南长沙·高一长沙市明德中学校联考期末）已知函数，则（    ）
A．
B．
C．的图象可以看作是由的图象向左平移而得到
D．如果将看成某个简谐运动，则这个简谐运动的频率为
【答案】ACD
【分析】利用三角恒等变换可判断AB选项，利用三角函数图象变换可判断C选项，利用正弦型函数的周期公式可判断D选项.
【详解】因为
，
因为，所以，的图象可以看作是由的图象向左平移而得到，
将看成某个简谐运动，则这个简谐运动的频率为，
所以ACD正确，B不正确．
故选：ACD．
28．（2022秋·湖南株洲·高一株洲二中校考期末）下列各式中，值为的是（    ）
A． B．
C． D．
【答案】ABC
【分析】根据诱导公式，结合两角和的正弦公式、正切公式逐一判断即可.
【详解】对于A，，故A正确；
对于B，，故B正确：
对于C，，故C正确；
对于D，
，故D错误；
故选：ABC
29．（2022秋·湖南岳阳·高一统考期末）下列结论正确的是（    ）
A．函数是以为最小正周期，且在区间上单调递减的函数
B．若是斜三角形的一个内角，则不等式的解集为
C．函数的单调递减区间为
D．函数的值域为
【答案】AC
【分析】根据正弦函数的周期性和单调性可判断A正确；根据正切函数的单调性可判断B，C正确；根据正弦函数的性质可判断D错.
【详解】A选项，函数的图象是在的图象基础上，将轴下方的部分翻折到轴上方，因此周期减半，即的最小正周期为；当时，，显然单调减；故A正确；
B选项，因为是斜三角形的一个内角，所以或；由得，所以或；故B错；
C选项，由得，即函数的单调递减区间为，故C正确；
D选项，因为，所以，因此，所以，故D错.
故选：AC.
30．（2022秋·湖南株洲·高一株洲二中校考期末）设函数（），则下列叙述正确的是（    ）
A．的最小正周期为 B．的图象关于直线对称
C．在上的最小值为 D．的图象关于点对称
【答案】ABD
【分析】根据正弦型函数的周期公式、对称性、最值逐一判断即可.
【详解】∵，∴，又，∴，∴；
对于A，的最小正周期，A正确；
对于B，因为，所以的图象关于直线对称，B正确；
对于C，当时，，则当，即时，，C错误；
对于D，当时，，此时，∴的图象关于点对称，D正确.
故选：ABD
31．（2022秋·湖南益阳·高一统考期末）已知函数， 则（    ）
A．当时，函数取得最大值2 B．函数在上为增函数
C．函数的最小正周期为 D．函数的图象关于原点对称
【答案】ACD
【分析】代入，计算出，A正确；利用整体法得到，数形结合得到其不单调，B错误；利用求出最小正周期，C正确；先求出定义域，结合得到D正确.
【详解】对A，当时，函数为的最大值，A正确；
对B，当时，，因为在上不单调，故在上不单调，B错误；
对C，由，故函数的最小正周期为，C正确；
对D，的定义域为R，且，
故函数的图象关于原点对称，D正确.
故选：ACD
32．（2022秋·湖南邵阳·高一统考期末）若将函数的图象向左平移个单位长度，得到函数的图象，则下列说法正确的是（    ）
A．的最小正周期为 B．在区间上单调递减
C．不是函数图象的对称轴 D．的图象关于点对称
【答案】ACD
【分析】根据函数图象的平移变换得出的图象，再利用
的性质结合周期公式逆推即可求解.
【详解】将函数的图象向左平移个单位长度，
得到函数的图象.
对于A，的周期为，故A正确；
对于B，由，得，从而
即时，单调递减，故B不正确；
对于C，，
所以不是函数图象的对称轴，故C正确；
对于D，，
所以的图象关于点对称，故D正确.
故选：ACD.
33．（2022秋·湖南衡阳·高一衡阳市一中校考期末）已知函数，将的图象向右平移个单位长度后得到函数的图象，则（    ）
A．的图象关于轴对称 B．的最小正周期是
C．的图象关于点对称 D．在上单调递减
【答案】BCD
【分析】根据余弦函数图象的平移变换可得的解析式，结合余弦函数的奇偶性、周期、对称性以及单调性一一判断各选项，即可得答案.
【详解】将的图象向右平移个单位长度后得到的图象，则,
该函数不是偶函数，最小正周期为，则A错误，B正确.
令，，解得，，当时，，
即的图象关于点对称，则C正确.
令，，解得，，
当时，即得在上单调递减，则D正确.
故选：BCD.
34．（2022秋·湖南长沙·高一长郡中学校考期末）已知函数（其中）的部分图象如图所示，则下列结论正确的是（    ）

A．
B．要想得到的图象，只需将的图象向左平移个单位
C．函数在区间上单调递增
D．函数在区间上的取值范围是
【答案】AC
【分析】由图得、，点在图象上求得及的解析式可判断A；根据图象平移规律可判断B；利用正弦函数的单调性可判断C；根据的范围求得可判断D.
【详解】由图得，所以，，
所以，因为点在图象上，所以，
，因为，所以，可得，故A正确；
对于B，将的图象向左平移个单位，得到的图象，故B错误；
对于C，由得，
所以函数在区间上单调递增，故C正确；
对于D，时，，所以，
函数在区间上的取值范围是，故D错误.
故选：AC.
35．（2022秋·湖南·高一校联考期末）已知函数，则下列结论错误的是（    ）
A．的最小正周期是
B．的图象关于点对称
C．在上单调递增
D．是奇函数
【答案】BCD
【分析】将化为只含有一个三角函数的形式，从而可求得其周期，判断A；将代入解析式中，看的值是否为1，判断B;求出函数的单调增区间，可以判断C;写出的展开式，判断其是否为奇函数，判断D.
【详解】,
因为，所以结论正确；
因为，所以的图象不关于点对称，
所以B结论错误；
令，解得，
当时，，因为，，
所以在上不单调，故结论错误；
因为，所以不是奇函数，
则中结论错误，
故选：BCD.
36．（2022秋·湖南衡阳·高一统考期末）若函数的最小值为，则的值可为（    ）
A． B． C． D．
【答案】BC
【分析】应用二倍角余弦公式可得，结合余弦函数、二次函数的性质及已知最小值，讨论与区间的位置关系，求的值.
【详解】由题设，，
令，则，其开口向上且对称轴为，
当时，，则；
当时，，则或(舍)；
当时，，则不合前提；
综上，或.
故选：BC
37．（2022秋·湖南长沙·高一长沙麓山国际实验学校校考期末）已知函数，则下列有关说法正确的是（    ）
A．若函数在区间上单调递增，则的最小值为
B．若函数在区间上单调递增，则的最大值为
C．若函数的图象向右平移个单位长度得到偶函数，则的最小值为
D．若函数在区间上有且只有个零点，则的取值范围是
【答案】BC
【分析】利用三角恒等变换化简函数的解析式，利用正弦型函数的单调性求出的取值范围，可判断AB选项；求出平移后的函数解析式，利用正弦型函数的奇偶性可判断C选项；根据函数在区间上的零点个数求出的取值范围，可判断D选项.
【详解】.
对于AB选项，当时，，
因为函数在区间上单调递增，则，
所以，，解得，
因为，解得，，则，所以，，A错B对；
对于C选项，将函数的图象向右平移个单位长度得到函数，
函数为偶函数，则，解得，
当时，取最小值，C对；
对于D选项，当时，，
因为函数在区间上有且只有个零点，则，解得，D错.
故选：BC.
38．（2022秋·湖南湘潭·高一湘潭一中校联考期末）已知函数，则下列结论正确的是（    ）
A．是奇函数
B．的定义域是
C．在上单调递增
D．的图象的对称中心是，
【答案】ACD
【分析】利用奇函数的定义及诱导公式判断A；利用正切函数的性质判断BCD.
【详解】对于B，令，得，
可知的定义域为，故B错误；
对于A，定义域关于原点对称，且，故是奇函数，故A正确；
对于C，令，解得，
当时，在上单调递增，故C正确；
对于D，，得，即的图象的对称中心是，故D正确；
故选：ACD
39．（2022春·湖南常德·高一统考期末）已知函数（其中，，）的部分图象如图所示，则下列结论正确的是（    ）

A．函数f(x)的图象的周期为
B．函数f(x)的图象关于点（，0）对称
C．函数f(x)在区间[－，]上的最大值为2
D．直线与）图像所有交点的横坐标之和为
【答案】AC
【分析】先利用函数图象 ，从而求得函数解析式，然后利用零点，对称性及正弦三角形最值求解得结果.
【详解】依题意，，得，故A正确；
，，则，当时，取最小值，
则，得，即，
当时，，故B错误；
当[－，]，则，则，故C正确；
，则，设直线与）图像所有交点的横坐标为，则，解得，故D错误；
故选：AC.
40．（2022春·湖南衡阳·高一统考期末）已知函数，下列说法正确的是（    ）
A．的最大值为1 B．2π是的周期
C．关于，对称 D．在上单调递增
【答案】ABD
【分析】求得的最大值判断选项A；依据周期定义判断选项B；举反例否定选项C；依据复合函数单调性判定规则判断选项D.
【详解】定义域为，
选项A：的单调递增区间为，
单调递减区间为，
则在，时取得最大值.判断正确；
选项B：由
可得2π是的周期.判断正确；
选项C：由定义域为
可得点在图象上，
但关于的对称点不在图象上，
则不关于，对称.判断错误；
选项D：当时，单调递增，且，则单调递增，
则当时，单调递增.判断正确.
故选：ABD
41．（2022秋·湖南怀化·高一校联考期末）已知函数（其中，，），，恒成立，且在区间上单调，则下列说法正确的是（    ）
A．存在，使得是偶函数 B．
C．是奇数 D．的最大值为
【答案】BCD
【分析】根据题意得为对称中心，为对称轴，列出方程组进而可得为奇数，根据在区间上单调得，进而对逐一分析即可.
【详解】由已知得 是图像的一个对称中心，
直线是图像的一条对称轴，所以
，
则，于是，即为奇数，故C正确；
因为在区间上单调，
所以 得，
当时，由于 ，
所以，即，
在上单调，但不是偶函数，满足 ；
当时，由于，
所以，即 ，
在上单调，但不是偶函数，满足 ；
当时，由于，
所以，即 ，
此时在上不单调，故不合题意；
当时，由于，
所以 ，即 ，
此时在上不单调，故不合题意；
综上，选项A错误，选项B和D正确；
故选：BCD.
42．（2022春·湖南衡阳·高一校联考期末）设函数，已知在上有且仅有4个零点，则（    ）
A．的取值范围是
B．的图象与直线在上的交点恰有2个
C．的图象与直线在上的交点恰有2个
D．在上单调递减
【答案】AB
【分析】对于A,确定，根据零点个数确定，求得参数范围；对于B，C，采用整体代换思想，结合余弦函数的图象和性质即可判断；对于D，当时，确定，计算的范围，从而确定在上单调性.
【详解】当时，，因为在上有且仅有4个零点，
所以，解得，故A正确；
又由以上分析可知，函数在上有且仅有4个零点，
且，则在上，出现两次最大值，
此时函数的大致图象如图示：

即在上两次出现最大值1，即取时，取最大值，
故的图象与直线在上的交点恰有2个，故B正确；
由于当时，，，
当时，取最小值 ，由于是否取到不确定，
故的图象与直线在上的交点可能是1个或2个，故C错误；
当时， ，
因为，所以，，
故的值不一定小于，
所以在上不一定单调递减.
故选：AB.
【点睛】本题考查了复合型余弦函数的解析式中参数的确定以及零点以及最值和单调性问题，综合性强，计算量大，解答时要能综合应用三角函数的相关知识灵活解答，关键是整体代换思想的应用.

三、填空题
43．（2022春·湖南长沙·高一雅礼中学校联考期末）________．
【答案】##
【分析】先利用诱导公式化简，再利用差角公式求解.
【详解】.
故答案为：
44．（2022秋·湖南衡阳·高一衡阳市一中校考期末）函数的定义域为___________.
【答案】
【分析】先得到使函数有意义的关系式，求解即可.
【详解】若使函数有意义，需满足：，
解得；
故答案为：
45．（2022春·湖南株洲·高一株洲二中校考期末）将函数的图象向左平移个单位长度，再将图象上每个点的横坐标变为原来的倍纵坐标不变，得到函数的图象，若函数在区间上有且仅有一个零点，则的取值范围为_______．
【答案】
【分析】先根据图象的变换原则得到的解析式为，再由在区间上有且仅有一个零点，根据可判断，即可求解.
【详解】解：将函数的图象向左平移个单位长度，可得的图象；
再将图象上每个点的横坐标变为原来的倍（纵坐标不变），得到函数的图象，
若函数在区间上有且仅有一个零点，
因为，
所以，即，
故答案为：
46．（2022春·湖南衡阳·高一校联考期末）已知，则___________.
【答案】##-0.5
【分析】由两角和的正切公式，展开化简，可得，所求上下同除，计算即可得答案.
【详解】由，解得，
所以
故答案为：
47．（2022秋·湖南长沙·高一长沙麓山国际实验学校校考期末）已知，则___________.
【答案】##-0.5
【分析】根据给定条件，利用诱导公式及二倍角的余弦公式计算作答.
【详解】因，所以.
故答案为：
48．（2022秋·湖南长沙·高一长郡中学校考期末）已知，，且，，则的值是___________.
【答案】
【分析】由平方关系求得，，再求出即可得解.
【详解】解：因为，，且，，
所以，，且，
则，
所以.
故答案为：.
49．（2022秋·湖南长沙·高一湖南师大附中校考期末）设是第二象限角，为其终边上一点，且，则______.
【答案】##
【分析】根据三角函数定义，求得，以及，再结合正切的倍角公式，即可求得结果.
【详解】根据题意，，解得或或，又是第二象限角，故；
则，则.
故答案为：.
50．（2022秋·湖南岳阳·高一统考期末）如果函数同时满足下列两个条件：①函数图象关于直线对称；②函数图象关于点对称，那么我们称它为“点轴对称型函数”.请写出一个这样的“点轴对称函数”___________.
【答案】或
【分析】根据题意，设，由“点轴对称型函数”的定义可知的图象关于直线对称，且关于点对称，从而得出，当时，解方程求出，即可得出的解析式.
【详解】解：根据题意，设，
由于的图象关于直线对称，且关于点对称，
则，即，
当时，解得：，
所以或.
故答案为：或.
51．（2022秋·湖南衡阳·高一统考期末）已知函数的图象在上恰有两个最高点，则的取值范围为___________．
【答案】
【分析】根据区间上，求出的范围，由于在区间上恰有2个最高点，建立不等式关系，求解即可．
【详解】因为，所以，
依题意得，解得．
故答案为：.
52．（2022秋·湖南长沙·高一长郡中学校考期末）函数的最小正周期，则__________.
【答案】±2
【分析】根据正弦型函数的周期公式求解.
【详解】因为，
所以，解得，
故答案为：.
53．（2022秋·湖南岳阳·高一统考期末）请写出一个函数，使它同时满足下列条件：（1）的最小正周期是4；（2）的最大值为2．____________．
【答案】（答案不唯一）
【分析】由题意知函数振幅为2，，符合题意即可.
【详解】∵的最小正周期是4，∴；
∴的最大值为2，∴，
故可取,
故答案为：(答案不唯一)
54．（2022春·湖南长沙·高一长沙一中校考期末）已知函数的部分图象如图所示，将该函数的图象向左平移t（）个单位长度，得到函数的图象．若函数的图象关于原点对称，则t的最小值为________．

【答案】
【分析】由图象可得时，函数的函数值为0，可以解出的表达式，再利用平移的知识可以得出的最小值．
【详解】解：由图象可得时，函数的函数值为0，即，
，
，将此函数向左平移个单位得，，
又为奇函数，
，
，
的最小值是．
故答案为：.
55．（2022秋·湖南长沙·高一长沙麓山国际实验学校校考期末）已知函数的部分图象如图所示，将的图象向左平移个单位得到的图象，若不等式在，上恒成立，则的取值范围是 __．

【答案】
【分析】先根据图象的变换规律求出的解析式，进而求出在上的值域，再利用换元法，结合函数性质，求出最值解决问题．
【详解】解：依题意有，
，
所以，所以，
由图知，函数的最小正周期满足：，
所以，则，令得，
所以，
所以，
当时，，
故，所以，
令，
原不等式即化为在，上恒成立，
令，该二次函数开口向上，要使上式恒成立，只需：
，解得，
故的范围是．
故答案为：．