

2021北京门头沟五年级(上)期末数学(教师版)
展开这是一份2021北京门头沟五年级(上)期末数学(教师版),共8页。试卷主要包含了填空题,选择题,口算和估算,脱式计算,解方程或比例,作图题,图形计算,解答题等内容,欢迎下载使用。
2021北京门头沟五年级(上)期末
数 学
一、填空题
1.14.1÷11 的商用简便记法写作 , 得数保留三位小数的是 。
2.在横线上填上“>”、“<”或者“=”。
0.01×5.1 5.1×1.01 18.54÷9.27 9.27÷18.54
3.垚垚买了4支钢笔,每支a元;又买了5本练习本,每本b元,一共花的钱数可以用式子 来表示,当a=30,b=1.2时,一共应付 元。
4.如图所示,估一估门头沟占地面积大约是 平方千米。(每个小正方形的面积表示50平方千米)
5.从一个上底是8厘米,下底是10厘米,高是h厘米的梯形里剪去一个三角形,剪去部分的面积最大是 平方厘米。
二、选择题
6.下列式子中,( )是方程。
A. 4.5x B. 4.5+5=9.5 C. 4.5x>9 D. 4.5x=9
7.投掷49次硬币,有40次正面朝上,9次反面朝上。那么,投掷第50次硬币时( )。
A. 一定正面朝上 B. 一定反面朝上 C. 正反面都有可能 D. 不可能是反面朝上
8.结果与 0.345÷0.05 相等的算式是( )。
A. 3.45÷0.05 B. 0.345÷0.5 C. 3.45÷0.5 D. 345÷5
9.计算42.84÷7 ,可以看作是把4284个百分之一平均分成7份,每份是( )个百分之一。
A. 6.12 B. 61.2 C. 612 D. 6120
10.在400米的环形跑道周围每隔5米插一面红旗,两面黄旗,一共需要插( )面红旗。
A. 79 B. 80 C. 81 D. 160
11.一个水瓶最多能装1.25升纯净水,要装32升纯净水,至少需要( )这样的瓶子。
A. 24 B. 25 C. 26 D. 27
12.滨河公园有柏树210棵,比柳树棵数的2倍少38棵,柳树有多少棵?如果设柳树有x棵。都么下列方程错误的是( )。
A. 2x-38=210 B. 2x=210+38 C. 2x-210=38 D. 2x+38=210
13.一堆圆木,最上层5根,最下层10根,每往下一层都比上一层多1根,这堆圆木共( )根.
A. 50 B. 45 C. 40 D. 55
14.已知 a×0.4=b÷0.4=c+0.4=d-0.4 ,那么 a 、 b 、 c 、 d 四个数中,最大的数是( )。
A. a B. b C. c D. d
15.如图,平行线之间有三个图形,请比较它们面积的大小( )。
A. A>B>C B. A>C>B C. B
16.口算。
4.07+5.3= 2.7×2= 20×0.05= 0.32÷0.08=
4.44-4= 1.6×4= 0.05×2.4= 5.01÷0.1=
2.9+8.1= 0.9×10= 40×1.1= 10÷0.4=
四、脱式计算
17.计算下面各题,能简算的要简算。
① 3.6÷1.8+1.2
② 1.25×32×2.5
③ 1.39×6.1+3.9×1.39
④ 1.2×(14.4-11.6)
⑤ 2.7×0.99
⑥ [60-(9.5+28.9)]÷0.18
五、解方程或比例
18.解方程。
4(x+2)=16.4
六、作图题
19.画一画。
(1)在方格纸上描出下面各点,并把这三个点顺次连接成一个封闭的三角形。
A(3,1),B(9,1),C(5,5)
(2)在方格纸上画一个平行四边形,使这个平行四边形的面积与三角形ABC的面积相等。
七、图形计算
20.如图中,大正方形的边长是10分米,小正方形边长是5分米,阴影部分的面积是多少平方分米?
八、解答题
21.明明全家开车从北京去北戴河旅游,全程约323千米。
22.彤彤买了40米红色彩带准备进行手工制作。她先用28.8米的彩带编了6个蝴蝶。然后准备用剩下的彩带编一些同心结。如果每个同心结需要用0.7米的彩带。彤彤可以编几个同心结?(用方程解答)
23.为提倡节约用电,供电公司实施了“阶梯用电”收费标准。莉莉家上月缴电费192元。莉莉家上月用电多少千瓦时?
“阶梯用电”收费标准
月用电量(千瓦时)
200千瓦时及200千瓦时以下部分
超过200千瓦时以上部分
每千瓦时电费(元)
0.54
0.7
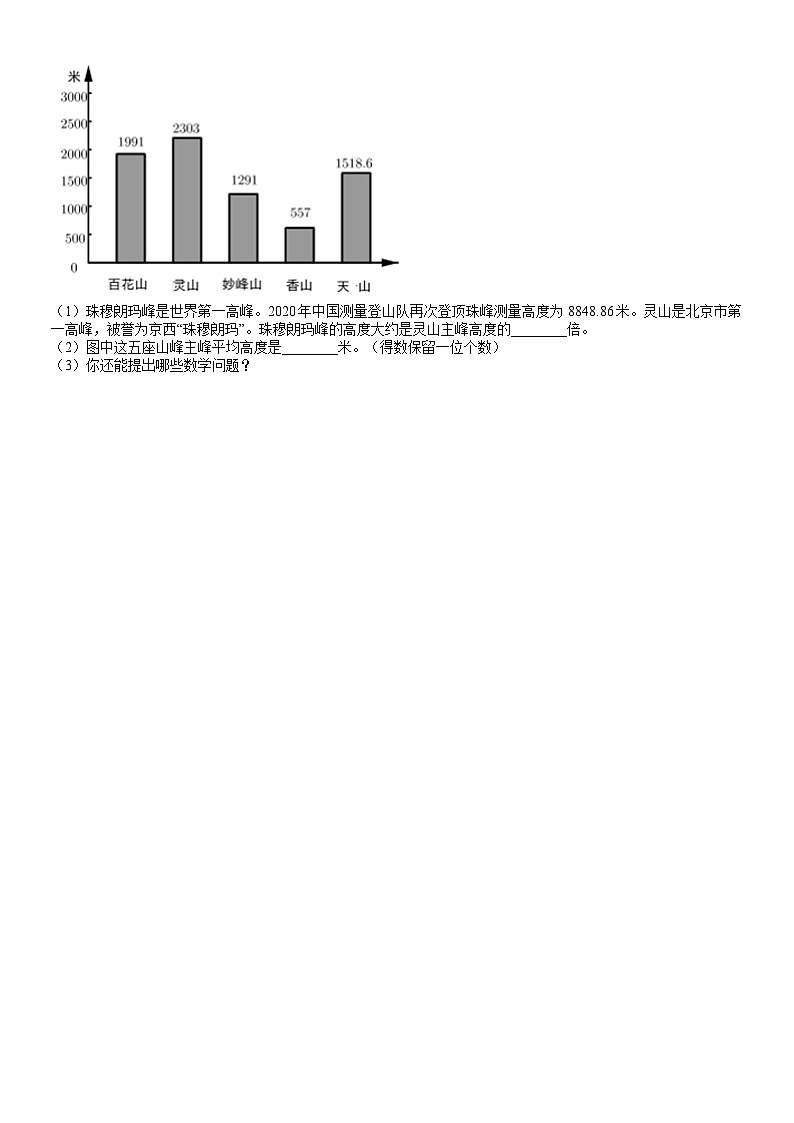
24.认真阅读下面统计图。回答问题。
北京地区部分山峰主峰高度统计图
(1)珠穆朗玛峰是世界第一高峰。2020年中国测量登山队再次登顶珠峰测量高度为8848.86米。灵山是北京市第一高峰,被誉为京西“珠穆朗玛”。珠穆朗玛峰的高度大约是灵山主峰高度的________倍。
(2)图中这五座山峰主峰平均高度是________米。(得数保留一位个数)
(3)你还能提出哪些数学问题?
2021北京门头沟五年级(上)期末数学
参考答案
一、填空题
1.【答案】 1.28•1•;1.282
【考点】循环小数的认识
【解析】【解答】14.1÷1=1.2818181......= 1.28•1• ,1.28•1•保留三位小数是1.282。
故答案为:1.28•1•;1.282。
【分析】一个循环小数的小数部分,依次不断循环出现的数字就是循环节,循环小数的简写形式是在循环节上面写点,保留三位小数,要看小数的第四位是几,根据四舍五入的方法去近似数。
2.【答案】 <;>
【考点】商的变化规律,积的变化规律
【解析】【解答】因为0.01<1.01,所以0.01×5.1<5.1×1.01;
因为18.54÷9.27>1,9.27÷18.54<1,所以18.54÷9.27>9.27÷18.54。
故答案为:<;>。
【分析】乘以相同的一个数(不为0),哪个数大,对应的积就大。
因为被除数大于除数,所以商大于1。被除数小于除数,所以商小于1,据此进行比较大小即可。
3.【答案】 4a+5b;126
【考点】用字母表示数,含字母式子的化简与求值
【解析】【解答】 垚垚买了4支钢笔,每支a元;又买了5本练习本,每本 b 元,一共花的钱数可以用式子4a+5b来表示, 当a=30,b=1.2时, 一共应付 4×30+5×1.2=120+6=126(元)。
故答案为:4a+5b;126。
【分析】根据单价×数量=总价,分别求出4支钢笔和5本练习本的钱数,再把两个钱数相加就是一共花的钱数。把a=30,b=1.2代入含有字母的式子,计算就是一共应付的钱数。
4.【答案】 1400
【考点】组合图形面积的巧算
【解析】【解答】18÷2+19=28(个),28×50=1400(平方千米)。
故答案为:1400。
【分析】可以通过数小正方形个数的方法计算,两个不完整的小正方形是1个正方形,把不完整的正方形和完整的正方形个数相加,再乘以50就是门头沟的占地面积。
5.【答案】 5h
【考点】三角形的面积
【解析】【解答】10×h÷2=5h。
故答案为:5h。
【分析】从一个梯形里剪去一个最大的三角形,三角形的底是梯形较长的底,高是梯形的高,根据三角形面积公式计算就是剪去的最大的三角形的面积。
二、选择题
6.【答案】 D
【考点】方程的认识及列简易方程
【解析】【解答】4.5x=9,符合方程的概念,是方程。
故答案为:D。
【分析】含有未知数的等式是方程,依据方程的概念解答即可。
7.【答案】 C
【考点】预测简单事件发生的可能性及理由阐述
【解析】【解答】根据随机事件发生的可能性与前面的发生没有关系, 硬币有两个面,投掷第50次硬币时正反面都有可能。
故答案为:C。
【分析】根据随机事件发生的独立性,可得投掷第50次硬币与前49次的结果无关;然后根据硬币只有正反两面,所以第50次硬币正面朝上的可能性是正反面都有可能。
8.【答案】 C
【考点】商的变化规律
【解析】【解答】A:3.45÷0.05≠0.345÷0.05;
B:0.345÷0.05≠0.345÷0.05;
C:3.45÷0.5=0.345÷0.05;
D:345÷5≠0.345÷0.05。
故答案为:C。
【分析】在除法算式中,被除数和除数同时扩大或缩小相同的倍数(0除外),商不变;据此解答即可。
9.【答案】 C
【考点】除数是整数的小数除法
【解析】【解答】计算42.84÷7时,可以把42.84看作4284个百分之一,4284÷7=612。
故答案为:C。
【分析】两位小数除以整数,先把小数看作整数,得到商后再把商缩小100倍即可。
10.【答案】 B
【考点】植树问题
【解析】【解答】解:400÷5=80面,所以一共需要插80面红旗。
故答案为:B。
【分析】在环形跑道上,一共插红旗的面熟=环形跑道的长度÷相邻两面红旗之间的距离,据此作答即可。
11.【答案】 C
【考点】商的近似数
【解析】【解答】32÷1.25=25(个).......0.75(升),25+1=26(个)。
故答案为:C。
【分析】 一个水瓶最多能装1.25升纯净水,要装32升纯净水, 就是求32里面有多少个1.25,根据除法的意义,用除法计算即可,要用“进一法”保留结果。
12.【答案】 D
【考点】列方程解含有一个未知数的应用题
【解析】【解答】解:D项中2x+38=210不正确。
故答案为:D。
【分析】题中存在的等量关系是:柳树的棵数×柏树的棵数是梨树的倍数-少的棵数=柏树的棵数,据此列出方程,然后进行变形即可。
13.【答案】 B
【考点】梯形的面积
【解析】【解答】解:10-5+1=6(层),(5+10)×6÷2=15×6÷2=45(根),所以这堆圆木一共有45根。
故答案为:B。
【分析】因为每往下一层都比上一层多1根, 那么可以把这堆圆木的形状看作是一个梯形,梯形的上底是5,下底是10,用最下层根数减去最上层根数加上1求出层数,也就是梯形的高,再根据梯形的面积公式:S=(a+b)h÷2, 把数据代入公式解答。
14.【答案】 A
【考点】小数乘整数的小数乘法,除数是小数的小数除法
【解析】【解答】解:假设a×0.4=b÷0.4=c+0.4=d-0.4=1,那么a=1÷0.4=2.5,b=1×0.4=0.4,c=1-0.4=0.6,d=1+0.4=1.4,a>d>c>b,所以最大的数是a。
故答案为:A。
【分析】本题可以假设它们最后的值是1,然后计算出a、b、c、d的值,最后比较它们的大小即可。
15.【答案】 B
【考点】平行四边形的面积,梯形的面积,平行的特征及性质,三角形的面积
【解析】【解答】解:设平行线间的距离是h,也就是三个图形的高都是h,
图A:S=ah;
图B:S=a×h÷2=ah2;
图C:设梯形的上底是b,梯形的上底小于a,S=(b+a)×h÷2=(a+b)h2。
所以A>C>B。
故答案为:B。
【分析】根据平行线间处处距离相等,可知图形的高是相等的,那么先假设出高,然后根据平行四边形的面积公式:S=ah,三角形的面积公式:S=a×h÷2,梯形的面积公式:S=(b+a)×h÷2,把数据分别代入公式求出它们的面积,最后进行比较即可。
三、口算和估算
16.【答案】 4.07+5.3=9.37 2.7×2=5.4 20×0.05=1 0.32÷0.08=4
4.44-4=0.44 1.6×4=6.4 0.05×2.4=0.12 5.01÷0.1=50.1
2.9+8.1=11 0.9×10=9 40×1.1=44 10÷0.4=25
【考点】除数是小数的小数除法
【解析】【分析】计算小数乘法,先按照整数乘法的计算方法计算出积,然后数出因数中一共有几位小数,就从积的末位数出几位,点上小数点即可;
计算除数是小数的小数除法,先移动除数的小数点,使它变成整数,除数的小数点向右移动几位,被除数的小数点也向右移动几位,然后按照除数是整数的小数除法计算即可。
四、脱式计算
17.【答案】 解:① 3.6÷1.8+1.2
=2+1.2
=3.2;
② 1.25×32×2.5
=(1.25×8)×(4×2.5)
=10×10
=100;
③ 1.39×6.1+3.9×1.39
=1.39×(6.1+3.9)
=1.39×10
=13.9;
④ 1.2×(14.4-11.6)
=1.2×2.8
=3.36;
⑤ 2.7×0.99
=2.7×(1-0.01)
=2.7×1-2.7×0.01
=2.7-0.027
=2.673;
⑥ [60-(9.5+28.9)]÷0.18
=[60-38.4]÷0.18
=21.6÷0.18
=120
【考点】小数的四则混合运算,小数乘法运算律
【解析】【分析】在没有小括号,既有加减法,又有乘除法的计算中,要先算乘除法,再算加减法;
在小数的连乘计算中,可以把乘起来是整数的数利用乘法交换律和结合律进行简便计算;
在有小括号的计算中,要先算小括号里面的,再算小括号外面的;
乘法分配律:a×b+a×c=a×(b+c);
在既有小括号,又有中括号的计算中,要先算小括号里面的,再算中括号里面的,最后算中括号外面的。
五、解方程或比例
18.【答案】 4(x+2)=16.4
解: 4(x+2)÷4=16.4÷4
x+2=4.1
x+2-2=4.1-2
x=2.1
【考点】综合应用等式的性质解方程
【解析】【分析】解方程时,可以先把相同的项放在一起计算,即把含有x的项放在等号的左边,把常数项放在等号的右边,然后等号两边同时除以x前面的数,就可以解得x的值。
六、作图题
19.【答案】 (1)
(2)解:6×4÷2=12
【考点】平行四边形的面积,数对与位置,三角形的面积
【解析】【分析】(1)用数对表示点的位置时,数对中第一个数字是几,就表示这个点在第几列,第二个数字是几,就表示这个点在第几行;
(2)三角形的面积=底×高÷2,平行四边形的面积=底×高,据此画出相应的平行四边形即可。
七、图形计算
20.【答案】 解:5×10÷2
=50÷2
=25(平方分米)
【考点】三角形的面积
【解析】【分析】从图中可以看出,阴影部分是三角形的面积,其中三角形的底=小正方形的边长,三角形的高=大正方形的边长,三角形的面积=底×高÷2,据此代入数据作答即可。
八、解答题
21.【答案】 解:30.5×9.8=298.9(千米)
298.9千米<323千米
答:中途需要加油。
【考点】小数乘小数的小数乘法
【解析】【分析】本题可以先计算出汽车油箱里的油一共可以行驶的里程,即用每升汽油的行驶里程×汽油升数,然后与全程进行比较即可。
22.【答案】 解:设彤彤可以编x个同心结。
28.8+0.7x=40
0.7x=11.2
x=16
答:彤彤可以编16个同心结。
【考点】列方程解含有一个未知数的应用题
【解析】【分析】本题可以设彤彤可以编x个同心结,题中存在的等量关系是:编蝴蝶用的彩带长度+编同心结的个数×每个同心结需要用到的彩带的长度=彩带的总长度,据此代入数据和字母作答即可。
23.【答案】 解:(192-200×0.54)÷0.7
=(192-108)÷0.7
=84÷0.7
=120(千瓦时)
200+120=320(千瓦时)
答:莉莉家上月用电320千瓦时。
【考点】小数的四则混合运算
【解析】【分析】超过200千瓦时花的钱数=莉莉家上月缴的电费-200×200千瓦时及200千瓦时以下部分每千瓦时的价钱,所以超过200千瓦时的用电量=超过200千瓦时花的钱数÷超过200千瓦时以上部分每千瓦时的价钱,所以莉莉家上月的用电量=200+超过200千瓦时的用电量,据此代入数据作答即可。
24.【答案】 (1)4
(2)1532.1
(3)解:这五座山峰主峰最高峰和最低峰的主峰分别是多少米?
最高峰主峰是2303米,最低峰主峰是557米。
【考点】平均数的初步认识及计算,从单式条形统计图获取信息
【解析】【解答】解:(1)8848.86÷2303≈4, 珠穆朗玛峰的高度大约是灵山主峰高度的4倍。
(2)(1991+2303+1291+557+1518.6)÷5≈1532.1(米),
图中这五座山峰主峰平均高度是 1552.1米。
故答案为:(1)4;(2)1532.1。
【分析】(1)珠穆朗玛峰的高度大约是灵山主峰高度的倍数=珠穆朗玛峰的高度÷灵山主峰的高度,据此代入数据作答即可;
(2)这五座山峰主峰平均高度就是把这五座山峰的高度加起来,然后再除以5即可;
(3)题中给出了五座山峰主峰的高度,可以提的问题是这五座山峰主峰最高峰和最低峰的主峰分别是多少米?然后根据题中所给的图作答即可。
相关试卷
这是一份2021北京西城五年级(上)期末数学(教师版),共18页。试卷主要包含了填空,按要求计算,按要求做,解决问题等内容,欢迎下载使用。
这是一份2021北京通州五年级(上)期末数学(教师版),共13页。试卷主要包含了填空,选择,计算,解决问题等内容,欢迎下载使用。
这是一份2021北京丰台五年级(上)期末数学(教师版),共16页。试卷主要包含了 直接写出得数, 0, 的循环节是, 把8个0, 盒子里有六个完全一样白球, 一列火车5分钟行驶12等内容,欢迎下载使用。













