2022-2023学年四川省成都市锦江区九年级（上）期末数学试卷（一诊）（含解析）

这是一份2022-2023学年四川省成都市锦江区九年级（上）期末数学试卷（一诊）（含解析），共29页。试卷主要包含了C，等内容，欢迎下载使用。
2022-2023学年四川省成都市锦江区九年级（上）期末数学试卷（一诊）
学校:___________姓名：___________班级：___________考号：___________
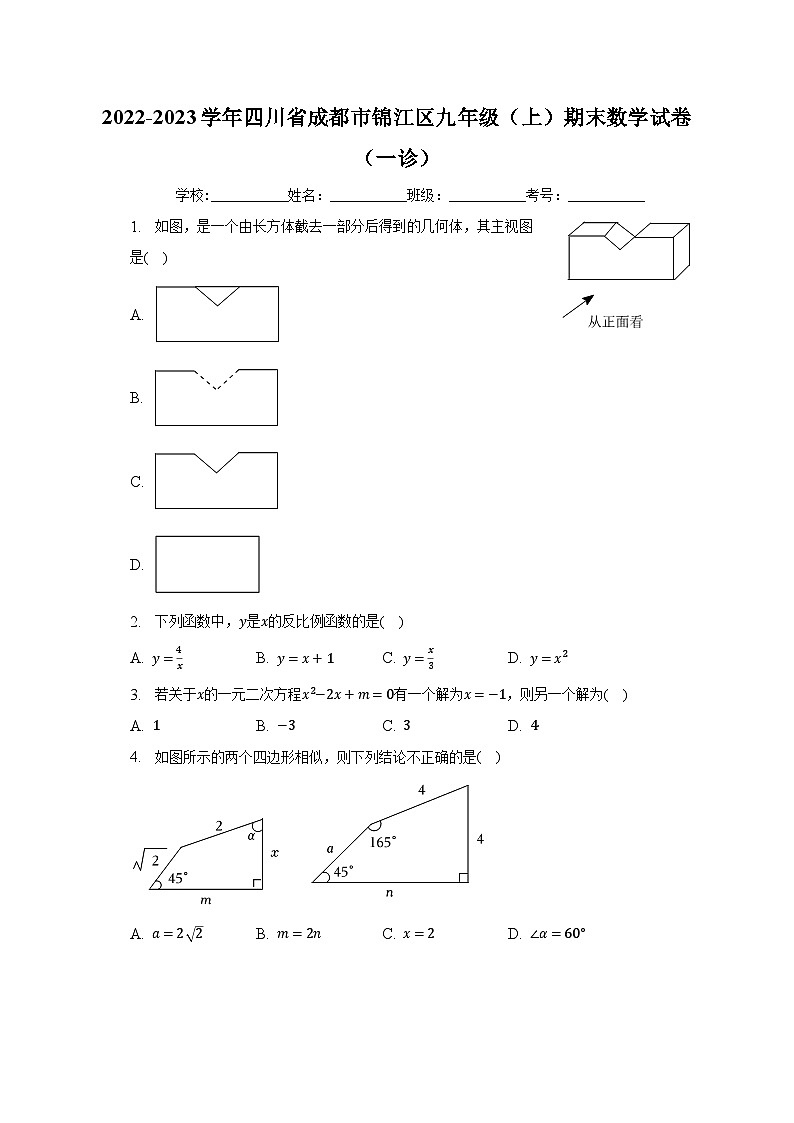
1. 如图，是一个由长方体截去一部分后得到的几何体，其主视图是(    )
A.
B.
C.
D.
2. 下列函数中，y是x的反比例函数的是(    )
A. y=4x B. y=x+1 C. y=x3 D. y=x2
3. 若关于x的一元二次方程x2−2x+m=0有一个解为x=−1，则另一个解为(    )
A. 1 B. −3 C. 3 D. 4
4. 如图所示的两个四边形相似，则下列结论不正确的是(    )

A. a=2 2 B. m=2n C. x=2 D. ∠α=60°
5. 如图，已知在平面直角坐标系中，四边形ABCD是菱形，其中点B的坐标是(6,2)，点D的坐标是(0,2)，点A在x轴上，则点C的坐标是(    )
A. (3,2)
B. (3,3)
C. (3,4)
D. (2,4)
6. 一个不透明的箱子里装有m个球，其中红球3个，这些球除颜色不同其余都相同，每次搅拌均匀后，任意摸出一个球记下颜色后再放回，大量重复试验发现，摸到红球的频率稳定在0.2附近，则可以估算出m的值为(    )
A. 10 B. 15 C. 20 D. 25
7. 如图，在方格纸上，以点O为位似中心，把线段AB缩小到原来的12，则点A的对应点为(    )

A. 点D或点G B. 点E或点F C. 点D或点F D. 点E或点G
8. 如图，在矩形ABCD中，AB=6，BC=8.对角线AC，BD相交于点O.点E，F分别是AO，AD的中点，连接EF，则△AEF的周长为(    )
A. 6
B. 7
C. 8
D. 9
9. 若ba=2，则ba+b= ______ ．
10. 关于x的一元二次方程(x−1)2=a+1有两个不相等的实数根，则a的取值范围是______ ．
11. 已知点A(x1,y1)，B(x2,y2)都在反比例函数y=3x的图象上，且x10)的图象上，顶点B在x轴正半轴上，边AO，AB分别交函数y=1x(x>0)，y=4x(x>0)的图象于点M，N.连接MN，若MN//x轴，则△AOB的面积为______ ．

22. 如图，在矩形ABCD中.AB=6，BC=12，点P是DC上一点，且DP=5，点E，F分别是AD，BC上的动点，连接EF，AP，始终满足EF⊥AP.连接AF，PF，PE，记四边形AEPF的面积为S1，记△ABF的面积为S2，记△FCP的面积为S3，记△EDP的面积为S4．S1S2+S3+S4= ______ ．

23. 如图，在平面直角坐标系xOy中，正方形ABCD的顶点A，C的坐标分别为A(−1,1).C(1,−1)，已知线段MN的端点M，N的坐标分别为M(3,3)，N(72,32)，平移线段MN，使得平移后的线段的两个端点均落在正方形ABCD的边上，此时正方形ABCD被该线段分为两部分，其中三角形部分的面积为______ ；已知线段PQ的端点坐标分别为P(x1,y1)，Q(x2,y2)，且x1≠x2，y1≠y2，PQ=2.平移线段PQ，使得平移后的线段P′Q′的两个端点均落在正方形ABCD的边上，且线段P′Q′将正方形的ABCD面积分为6：19部分，取P′Q′的中点H，连接OH，则OH的长为______ ．

24. 电影《长津湖》是一部讲述抗美援朝题材影片，该片以朝鲜长津湖战役为背景，讲述一个志愿军连队在极寒严酷环境下坚守阵地奋勇杀敌、为战役胜利作出重要贡献的故事，2022年清明节来临之际，某电影院开展“清明祭英烈，共铸中华魂”系列活动，对团体购买该电影票实行优惠，决定在原定零售票价基础上每张降价16元，这样按原定零售票价需花费2000元购买的门票，现在只花费了1200元．
(1)求每张电影票的原定零售票价；
(2)为了弘扬爱国主义精神，该影院决定对网上购票的个人也采取优惠，原定零售票价经过连续两次降价后票价为每张32.4元，求平均每次降价的百分率．
25. 已知在平面直角坐标系xOy中，点(1,a)，(2,a−12)在反比例函数y=kx的图象上．
(1)求k的值；
(2)将反比例函数y=kx的图象中x轴下方部分沿x轴翻折，其余部分保持不变，得到新的函数图象如图1所示，新函数记为函数F．
①如图2，直线y=x+b与函数F的图象交于A，B两点，点A横坐标为x1，点B横坐标为x2，且x1≤x21)，连接DQ.若n2BP2+DQ2=(n2+1)AB2，求BPBD的值(用含n的代数式表示)．

答案和解析

1.【答案】C 
【解析】解：从正面看，可得选项C的图形，
故选：C．
根据从正面看得到的图形是主视图，可得答案．
本题考查了简单组合体的三视图，掌握从正面看得到的图形是主视图是关键．

2.【答案】A 
【解析】解：A、y=4x是反比例函数，k=4，
故A选项符合题意；
B、y=x+1是一次函数，不是反比例函数，
故B选项不符合题意；
C、y=x3是正比例函数，
故C选项不符合题意；
D、y=x2是二次函数，不是反比例函数，
故D选项不符合题意，
故选：A．
根据形如y=kx(k为常数，k≠0)的函数称为反比例函数，即可判断．
本题考查了反比例函数的定义，熟练掌握反比例函数的定义是解题的关键．

3.【答案】C 
【解析】解：设方程的另一个解为x1，
根据题意得：−1+x1=2，
解得：x1=3．
故选：C．
设方程的另一个解为x1，根据两根之和等于−ba，即可得出关于x1的一元一次方程，解之即可得出结论．
本题考查了根与系数的关系以及一元二次方程的解，牢记两根之和等于−ba、两根之积等于ca是解题的关键．

4.【答案】B 
【解析】解：∵两个四边形相似，
∴相似比为：2：4=1：2，
∴ 2：a=x：4=m：n=1：2，
解得：a=2 2，x=2，2m=n，
则∠α=360°−45°−90°−165°=60°，
综上所述：只有选项B符合题意．
故选：B．
根据相似图形的对应角相等，对应边的比相等得到答案．
本题考查了相似多边形的性质，牢记相似多边形的对应角相等，对应边的比也相等．

5.【答案】C 
【解析】解：连接AC，BD相交于点E，
∵四边形ABCD是菱形，
∴AE=CE，BE=DE，AC⊥BD，
∵点A在x轴上，点B的坐标为(6,2)，点D的坐标为(0,2)，
∴BD=6，AE=2，
∴DE=12BD=3，AC=2AE=4，
∴点C的坐标为：(3,4)．
故选：C．
首先连接AC，BD相交于点E，由在菱形ABCD中，点A在x轴上，点B的坐标为(6,2)，点D的坐标为(0,2)，可求得点E的坐标，继而求得答案．
此题考查了菱形的性质以及坐标与图形的性质．注意菱形的对角线互相平分且垂直．

6.【答案】B 
【解析】解：由题意知，m的值约为3÷0.2=15，
故选：B．
用红球的个数除以红球频率的稳定值即可．
本题主要考查利用频率估计概率，大量重复实验时，事件发生的频率在某个固定位置左右摆动，并且摆动的幅度越来越小，根据这个频率稳定性定理，可以用频率的集中趋势来估计概率，这个固定的近似值就是这个事件的概率．

7.【答案】A 
【解析】解：作射线AO，
，
射线AO经过点D和点G，且OD=12OA，OG=12OA，
∴点A的对应点为点D或点G，
故选：A．
作射线AO，根据位似中心的概念、线段的位似比解答即可．
本题考查位似变换，正确记忆位似图形的特征是解题关键．

8.【答案】D 
【解析】解：∵四边形ABCD是矩形，
∴AD=BC=8，∠BAD=90°，OB=OD=OA=OC，
在Rt△BAD中，∵BD= AB2+AD2= 62+82=10，
∴OD=OA=OB=5，
∵E.F分别是AO，AD中点，
∴EF=12OD=52，AE=52，AF=4，
∴△AEF的周长为9，
故选：D．
因为四边形ABCD是矩形，所以AD=BC=8，∠BAD=90°，OB=OD=OA=OC，在Rt△BAD中，可得BD=10，推出OD=OA=OB=5，因为E.F分别是AO.AD中点，根据三角形中位线定理即可得到结论．
本题考查三角形中位线定理、矩形的性质等知识，解题的关键是灵活运用所学知识解决问题，属于基础题，中考常考题型．

9.【答案】23 
【解析】解：∵ba=2，
∴b=2a，
∴ba+b=2aa+2a=23．
故答案为：23．
根据已知条件得出b=2a，再代入要求的式子进行计算，即可得出答案．
此题考查了比例的性质，解题的关键是用a表示出b．

10.【答案】a>−1 
【解析】解：整理方程得x2−2x−a=0，
∵关于x的一元二次方程(x−1)2=a+1有两个不相等的实数根，
∴Δ=4+4a>0，
解得a>−1．
故答案为：a>−1．
先将一元二次方程整理成一般形式，然后根据一元二次方程的定义和判别式的意义得到Δ>0，然后求出两个不等式的公共部分即可．
本题考查了根的判别式：一元二次方程ax2+bx+c=0(a≠0)的根与Δ=b2−4ac有如下关系：当Δ>0时，方程有两个不相等的实数根；当Δ=0时，方程有两个相等的实数根；当Δ