2023年河北省保定市雄安市容和红杰中学中考数学一模试卷（含解析）

这是一份2023年河北省保定市雄安市容和红杰中学中考数学一模试卷（含解析），共28页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2023年河北省保定市雄安市容和红杰中学中考数学一模试卷
第I卷（选择题）
一、选择题（本大题共16小题，共42.0分。在每小题列出的选项中，选出符合题目的一项）
1. 嘉嘉在测量∠PMQ的度数时，错误地将量角器摆放成如图所示的位置，则∠PMQ的度数(    )

A. 小于40° B. 大于40° C. 等于40° D. 无法确定
2. 已知a−b=a+3−14，则下列表示b的式子是(    )
A. 14−3 B. 3−14 C. 3+14 D. −14−3
3. 如图，点P在△ABC的AB边上从点A向点B移动，当S△APC=S△BPC时，则CP是△ABC的(    )


A. 中线 B. 角平分线 C. 高 D. 中位线
4. 某通信技术公司在测试5G网速时，发现其下载一个1KB的文件用时0.0000038s，若下载一个mKB的文件所用的时间可以用科学记数法表示为n×10−5s，则m的值可以是(    )
A. 2 B. 20 C. 200 D. 2000
5. 如图，△ABC与△DEC都是等边三角形，固定△ABC，将△DEC从图示位置绕点C逆时针旋转一周，在△DEC旋转的过程中，下列说法正确的是(    )
A. △DEC总与△ABC位似
B. △DEC与△ABC不会位似
C. 当点D落在CB上时，△DEC与△ABC位似
D. 存在△DEC的两个位置使得△DEC与△ABC位似

6. 若(2x−m)(x+1)的运算结果是关于x的二次二项式，则m的值等于(    )
A. −2或0 B. 2或0 C. −2或2 D. 2或−2或0
7. 如图是由大小相同的小正方体搭成的几何体，小明分别以A和B为正方向观察该几何体，则他从两个方向观察到的三视图(    )
A. 主视图相同，左视图不同，俯视图不同
B. 主视图不同，左视图相同，俯视图不同
C. 主视图不同，左视图不同，俯视图相同
D. 主视图相同，左视图相同，俯视图不同
8. 如左图的天平架是平衡的，其中同一种物体的质量都相等，如右图，现将不同质量的一“〇”和一个“”从通道的顶端同时放下，两个物体等可能的向左或向右落在下面的托盘中，此时两个托盘上物体的质量分别为y甲(g)和y乙(g)，则下列关系可能出现的是(    )


A. y甲=y乙 B. y甲=2y乙 C. 5y甲=6y乙 D. 3y甲=5y乙
9. 如图所示的运算程序中，甲输入的x为3a+2b，乙输入的x为−3a−2b，丙输入的x为2b−3a.若a>b>0，则输出结果相同的是(    )

A. 甲和乙 B. 甲和丙 C. 乙和丙 D. 三人均不相同
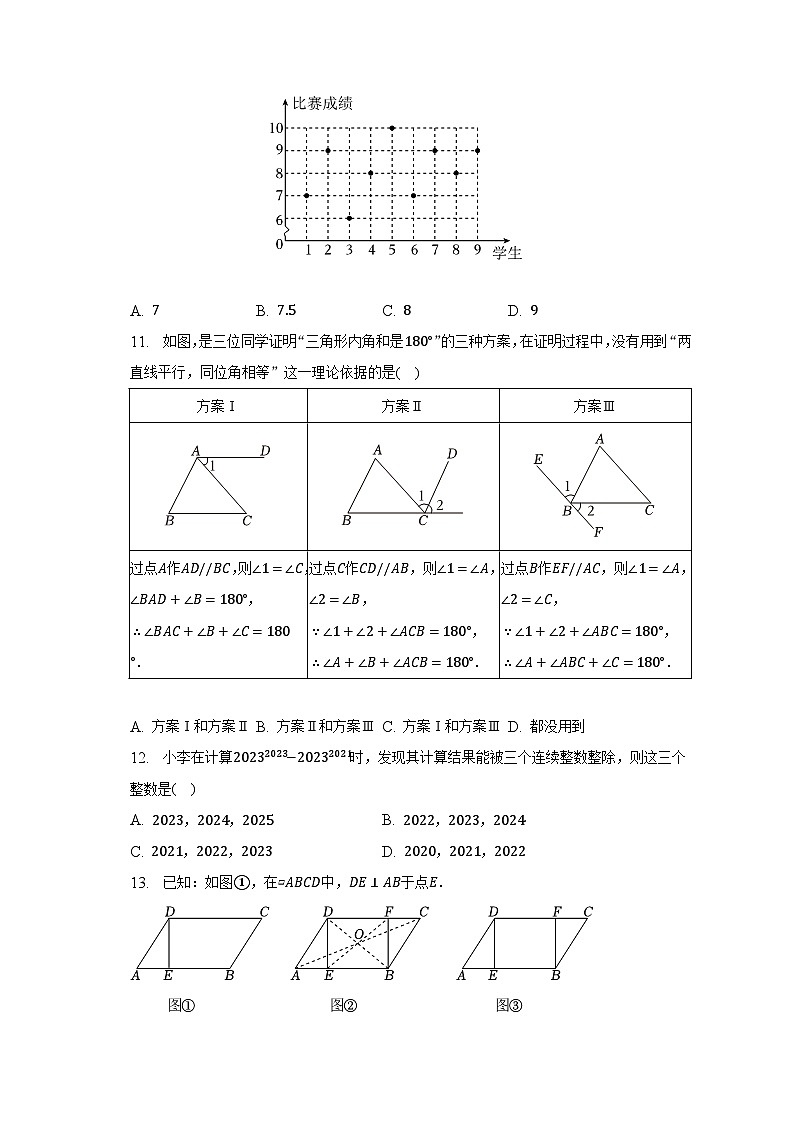
10. 某中学举办了以“放歌新时代奋进新征程”为主题的知识竞答比赛(共10道题，每题1分).已知选取了10名学生的成绩，且10名学生成绩的中位数和众数相同，但在记录时遗漏了一名学生的成绩.如图是参赛9名学生的成绩，则这10名学生成绩的中位数是(    )

A. 7 B. 7.5 C. 8 D. 9
11. 如图，是三位同学证明“三角形内角和是180°”的三种方案，在证明过程中，没有用到“两直线平行，同位角相等”这一理论依据的是(    )
方案Ⅰ
方案Ⅱ
方案Ⅲ



过点A作AD//BC，则∠1=∠C，∠BAD+∠B=180°，
∴∠BAC+∠B+∠C=180°．
过点C作CD//AB，则∠1=∠A，∠2=∠B，
∵∠1+∠2+∠ACB=180°，
∴∠A+∠B+∠ACB=180°．
过点B作EF//AC，则∠1=∠A，∠2=∠C，
∵∠1+∠2+∠ABC=180°，
∴∠A+∠ABC+∠C=180°．

A. 方案Ⅰ和方案Ⅱ B. 方案Ⅱ和方案Ⅲ C. 方案Ⅰ和方案Ⅲ D. 都没用到
12. 小李在计算20232023−20232021时，发现其计算结果能被三个连续整数整除，则这三个整数是(    )
A. 2023，2024，2025 B. 2022，2023，2024
C. 2021，2022，2023 D. 2020，2021，2022
13. 已知：如图①，在▱ABCD中，DE⊥AB于点E．

作图.用尺规在DC上作出点F.使得BF⊥DC于点F．
作法一：如图②，作两条对角线，交于点O，连接EO并延长，交DC于点F，连接BF．
作法二：如图③，在DC上截取CF=AE，连接BF．
下列说法正确的是(    )
A. 作法一，二都正确 B. 作法一，二都不正确
C. 只有作法一正确 D. 只有作法二正确
14. 如图1是嘉淇化简分式x2−4x2−4x+4⋅2x−x2x2+4x+4的部分计算过程，则在化简过程中的横线上依次填入的卡片(图2)序号为(    )


A. ④①② B. ③①② C. ③②① D. ④②①
15. 如图，在正六边形ABCDEF中，对角线CE和DF交于点G，以GE，GD为边，作正六边形GDHIJE，已知正六边形GDHIJE的周长为6 3，则正六边形ABCDEF的面积是(    )
A. 92
B. 9 32
C. 272
D. 27 32
16. 已知实数a，b，c满足a+2b=3c，则下列结论不正确的是(    )
A. a−b=3(c−b) B. a−c2=c−b
C. 若a>b，则a>c>b D. 若a>c，则b−a>c−a2
第II卷（非选择题）
二、填空题（本大题共3小题，共13.0分）
17. 已知：( 2+ 3)2=5+2 a，则a= ______ ．
18. 如图，A，B，C，D，E五个顶点均在小正方形组成的网格的格点上.若EF⊥BD于点F，且EF=1，则DE的长为______ ．


19. 某同学编写了一个程序：如图，在平面直角坐标系中，线段AB的端点A(0,6)，B(5,0).原点O处有一光点发射器向第一象限发射光点，光点均沿直线y=x方向飞行，飞行的距离由输入的数据p(p>0)决定(当p=1.5时，光点会沿运动方向飞行1.5个单位，当p=2时，光点会沿运动方向飞行2个单位，以此类推)，光点飞行结束后会向两边扩散，形成反比例函数y=kx(x>0)的图象．
(1)写出p与k的关系式：______ ；当p= 10时，光点飞行结束后形成的反比例函数的解析式为______ ；
(2)记线段AB与反比例函数y=kx(x>0)的图象所围成的区域(不含边界)为M.当M中有n个整点(横、纵坐标都是整数)时，区域M就会连续闪烁n次，某光点发射后与线段AB所形成的区域连续闪烁了5次，则p的取值范围是______ ．
三、解答题（本大题共7小题，共65.0分。解答应写出文字说明，证明过程或演算步骤）
20. (本小题8.0分)
如图，点A，B，C，D是单位长度为1的数轴上的四个连续整数点，其中一个点表示的数是0．
(1)若点B与点D表示的数的和为4，求表示的数为0的点；
(2)若这四个点所表示的数的和大于−12，求点B表示的数的最小值．

21. (本小题8.0分)
我们学过的一些代数公式，很多都可以通过表示几何图形面积的方法进行直观推导和解释.例如：平方差公式和完全平方公式．
【提出问题】如何用表示几何图形面积的方法推证：11+23+33+…+n3？
【规律探索】观察如图表示几何图形面积的方法，并填空；

【方法延伸】第四个可验证的等式为______ ；
【解决问题】请用上面表示几何图形面积的方法化简13+23+33+…+n3．
22. (本小题8.0分)
为了落实“作业、睡眠、手机、读物、体质”五项管理要求，了解学生的“读物”情况，某校调查了一个班学生每周的课外阅读时间，绘制成了不完整的条形图．
(1)若本班学生每周课外阅读时间的平均数为2.5h，请补全条形图；
(2)嘉嘉参与了本次调查，在(1)的条件下，求嘉嘉的课外阅读时间不少于3h的概率．
(3)将每周课外阅读时间为4h的学生视为“阅读达人”，本班的“阅读达人”中一人为女生，其余为男生，老师计划从中随机抽取两人参加市级的中学生诗歌大赛，小强认为选中的两名学生都是男生的概率大，请用列表或画树状图的方法验证他的结论是否正确．

23. (本小题10.0分)
花卉市场中，某花店出售太阳花和绣球花两种盆栽花卉.若一次购买的绣球花不超过20盆时，按原价销售，超过20盆时，超出的部分可享受一定的折扣，由于太阳花利润很低，所以无对应折扣，均按原价出售.设购买太阳花的总费用为y甲元，购买绣球花的总费用为y乙元，购买花卉的盆数为x盆，其函数图象如图所示．
(1)说明交点A的实际意义；
(2)当一次购买的绣球花超过20盆时，超出的部分打几折？
(3)某花园小区购买了相同盆数的太阳花和绣球花，已知两种花各自的花费相差10元，求该小区购买了多少盆太阳花．

24. (本小题10.0分)
如图，在△ABC中，AB=AC，∠BAC=120°，点D为边BC上一动点，连接AD，作△ADE，使∠ADE=∠BAC，且DE=DA，AE与BC交于点F．
(1)当AE⊥BC时，求证：BD=ED；
(2)当AD取最小值时，若AB=2，求AE的长；
(3)当∠BAD=∠CAF时，设点D到AB的距离为x，直接写出S△ABC的值(用含x的式子表示)．

25. (本小题10.0分)
如图，在平面直角坐标系中，线段AB的端点为A(−1,0)，B(2,3)，抛物线L：y=ax2+bx+3与y轴交于点C．
(1)当抛物线L经过A，B两点时，
①求抛物线L的解析式和顶点坐标；
②已知抛物线L′与抛物线L关于直线y=m成轴对称，且抛物线L′与x轴的两个交点之间的距离为6，求m的值；
(2)我们将与线段有两个交点且开口向上的抛物线称为线段的“伴随抛物线”，已知抛物线L是线段AB的“伴随抛物线”且经过点B，求a的取值范围．

26. (本小题11.0分)
如图①，已知线段AC=6，B，O是线段AC的三等分点，以O为圆心，OB长为半径在线段BC的上方作半圆O，以AB为边在AB的上方作正方形ABFE，将正方形ABFE沿AC所在直线水平向右移动．

(1)如图②，连接AF，当AF与半圆O相切时，设切点为D，求CD的长(结果保留π)；
(2)如图②，在平移的过程中，设BF与半圆O交于点M，连接OM，CM，当∠BOM=60°时，求CM的长；
(3)如图③，点G是半圆O上的一点，且到OC的距离为1，当点B到达点C后，正方形ABFE立即绕着点C顺时针旋转，当边AB旋转90°时停止，若正方形ABFE向右平移的速度为每秒2个单位长度，绕点C旋转的速度为每秒15°，求点G在正方形ABFE内(含边界)的时长．
答案和解析

1.【答案】B 
【解析】解：连接OQ，则∠POQ=40°，

又∵∠QMP是△OQM的外角，
∴∠QMP>∠POQ=40°，
故选：B．
连接OQ，运用三角形的外角大于任何一个与它不相邻的外角解题即可．
本题考查三角形的外角，掌握三角形外角的性质是解题的关键．

2.【答案】A 
【解析】解：∵a−b=a+3−14
∴两边同时减去a得：−b=+3−14
∴两边同时乘以−1得：b=−3+14
故选：A．
运用等式的基本性质解题即可．
本题考查等式的基本性质，掌握等式的基本性质是解题的关键．

3.【答案】A 
【解析】解：∵S△APC=S△BPC，
∴S△APC=12S△ABC，
∴AP=12AB(等高的两个三角形面积比等于底的比)，
∴CP是△ABC的中线．
故选：A．
利用三角形的中线把它分成面积相等的两个三角形解题即可．
本题考查三角形的中位线，三角形的面积，掌握三角形的中线分得的两个三角形面积相等是解题的关键．

4.【答案】B 
【解析】解：∵0.0000038=0.38×10−5，
∴m×0.0000038=0.38m×10−5=n×10−5，
∴0.38m=n，
∵1≤n−3c，
∴bb，
∴2a>2b，
∵3c=a+2b，
∴2a−3c>2b−(a+2b)，
整理得a>c，
∴a>c>b，故选项C正确，不符合题意；
由B知a−c2=c−b，
∵a>c，
∴a−c2>0，c−a0，
∴b0，即b−a