专题训练四　平面直角坐标系中图形面积的求法

这是一份专题训练四　平面直角坐标系中图形面积的求法，共9页。
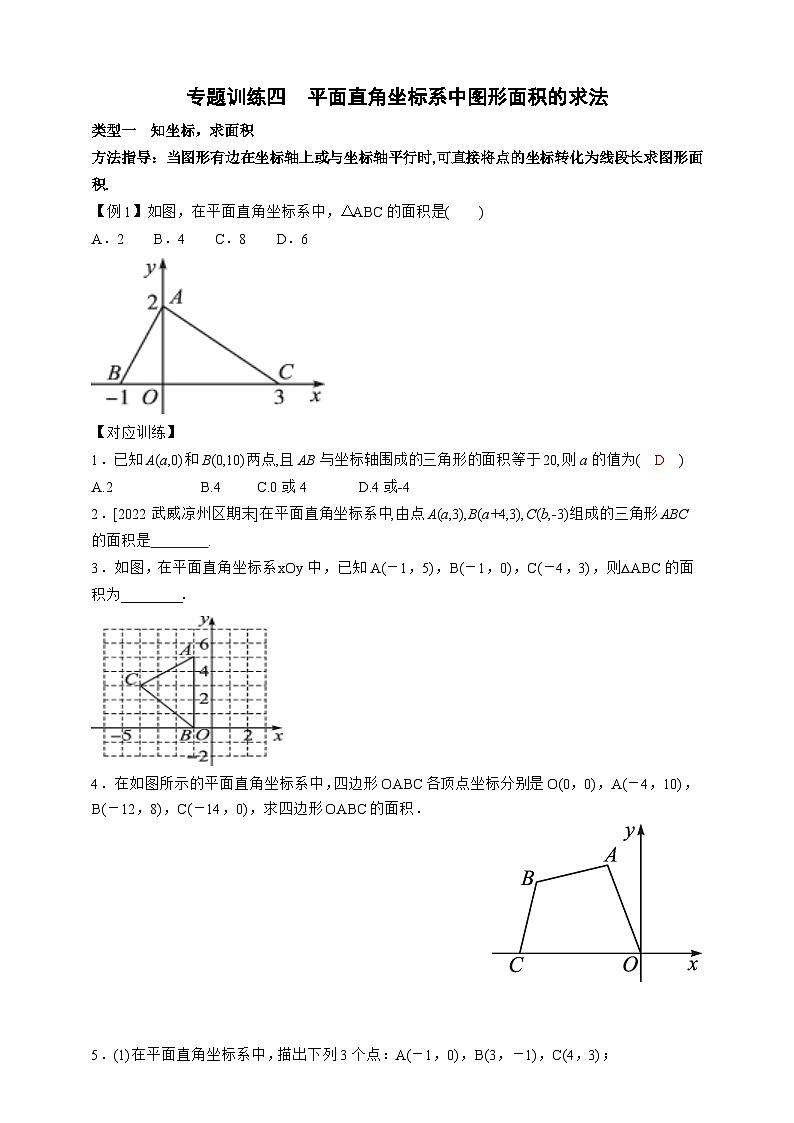
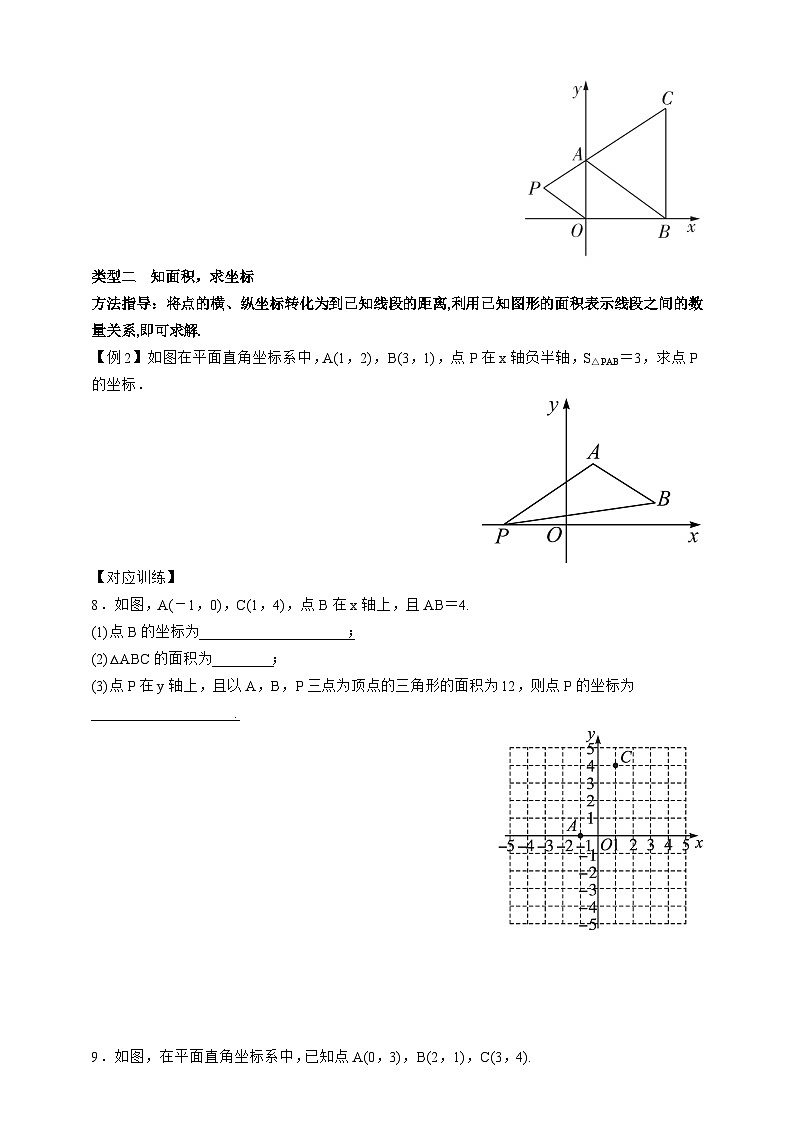
专题训练四　平面直角坐标系中图形面积的求法类型一　知坐标，求面积方法指导：当图形有边在坐标轴上或与坐标轴平行时,可直接将点的坐标转化为线段长求图形面积.【例1】如图，在平面直角坐标系中，△ABC的面积是(    )A．2    B．4    C．8    D．6【对应训练】1．已知A(a,0)和B(0,10)两点,且AB与坐标轴围成的三角形的面积等于20,则a的值为(　D　)A.2 B.4     C.0或4 D.4或-42．[2022武威凉州区期末]在平面直角坐标系中,由点A(a,3),B(a+4,3),C(b,-3)组成的三角形ABC的面积是　　　　. 3．如图，在平面直角坐标系xOy中，已知A(－1，5)，B(－1，0)，C(－4，3)，则△ABC的面积为________．4．在如图所示的平面直角坐标系中，四边形OABC各顶点坐标分别是O(0，0)，A(－4，10)，B(－12，8)，C(－14，0)，求四边形OABC的面积．  5．(1)在平面直角坐标系中，描出下列3个点：A(－1，0)，B(3，－1)，C(4，3)；(2)顺次连接A，B，C，组成△ABC，求△ABC的面积．6．[2022赣州期中]如图,已知三角形ABC的顶点坐标分别为A(-3,2),B(-1,-2),C(1,-1).将三角形ABC先向右平移3个单位长度,再向上平移1个单位长度,可以得到三角形A1B1C1.(1)在图中画出三角形A1B1C1;(2)三角形A1B1C1的顶点A1的坐标为　　　　,顶点C1的坐标为　　　　; (3)求三角形A1B1C1的面积;(4)已知点P在x轴上,以点A1,C1,P为顶点的三角形的面积为,求点P的坐标.7．[2022扬州江都区八校联考]如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a,b,c满足关系式+(b-3)2=0,(c-4)2≤0.(1)求a,b,c的值;(2)如果在第二象限内有一点P(-m,),请用含m的式子表示四边形ABOP的面积;(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与三角形ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.类型二　知面积，求坐标方法指导：将点的横、纵坐标转化为到已知线段的距离,利用已知图形的面积表示线段之间的数量关系,即可求解.【例2】如图在平面直角坐标系中，A(1，2)，B(3，1)，点P在x轴负半轴，S△PAB＝3，求点P的坐标．【对应训练】8．如图，A(－1，0)，C(1，4)，点B在x轴上，且AB＝4.(1)点B的坐标为____________________；(2)△ABC的面积为________；(3)点P在y轴上，且以A，B，P三点为顶点的三角形的面积为12，则点P的坐标为___________________ .    9．如图，在平面直角坐标系中，已知点A(0，3)，B(2，1)，C(3，4).(1)请在图中画出△ABC；(2)△ABC的面积为________；(3)若点P在x轴上，且△OCP的面积为△ABC面积的1.5倍，求点P的坐标．   10．如图，在平面直角坐标系中，A(a，0)，C(b，2)，且满足(a＋2)2＋＝0，过C作CB⊥x轴于B.(1)求△ABC的面积；(2)在y轴上是否存在点P，使得△ABC和△ACP的面积相等？若存在，求出P点坐标；若不存在，请说明理由． 
参考答案类型一　知坐标，求面积方法指导：当图形有边在坐标轴上或与坐标轴平行时,可直接将点的坐标转化为线段长求图形面积.【例1】如图，在平面直角坐标系中，△ABC的面积是(  B  )A．2    B．4    C．8    D．6分析：由图可知：△ABC点A的坐标为(0，2)，B的坐标为(－1，0)，点C的坐标为(3，0)，△ABC的底是BC＝4，高是OA＝2，由三角形的面积公式求得答案即可．【对应训练】1．已知A(a,0)和B(0,10)两点,且AB与坐标轴围成的三角形的面积等于20,则a的值为(　D　)A.2 B.4     C.0或4 D.4或-4【解析】∵A(a,0),B(0,10),∴OA=|a|,OB=10,∴S三角形AOB=OA×OB=×10|a|=20,解得a=±4.2．[2022武威凉州区期末]在平面直角坐标系中,由点A(a,3),B(a+4,3),C(b,-3)组成的三角形ABC的面积是　　　　. 【解析】∵点A(a,3),B(a+4,3),∴AB=4,∵C(b,-3),∴点C在直线y=-3上,∵直线AB:y=3与直线y=-3平行,且平行线间的距离为6,∴S三角形ABC=×4×6=12.【答案】123．如图，在平面直角坐标系xOy中，已知A(－1，5)，B(－1，0)，C(－4，3)，则△ABC的面积为________．【答案】7.54．在如图所示的平面直角坐标系中，四边形OABC各顶点坐标分别是O(0，0)，A(－4，10)，B(－12，8)，C(－14，0)，求四边形OABC的面积．解：过点A作AD⊥x轴，垂足为D，过点B作BE⊥x轴，垂足为E，则D(－4，0)，E(－12，0).∴BE＝8，AD＝10，OD＝4，DE＝8，CE＝2.∴S四边形OABC＝S△AOD＋S△BCE＋S梯形ABED＝OD·AD＋CE·BE＋(BE＋AD)·DE＝×4×10＋×2×8＋×(8＋10)×8＝1005．(1)在平面直角坐标系中，描出下列3个点：A(－1，0)，B(3，－1)，C(4，3)；(2)顺次连接A，B，C，组成△ABC，求△ABC的面积．解：(1)描点如图所示　(2)如图所示，S△ABC＝S梯形ADEC－S△ADB－S△BCE＝×(1＋4)×5－×1×4－×1×4＝12.5－2－2＝8.56．[2022赣州期中]如图,已知三角形ABC的顶点坐标分别为A(-3,2),B(-1,-2),C(1,-1).将三角形ABC先向右平移3个单位长度,再向上平移1个单位长度,可以得到三角形A1B1C1.(1)在图中画出三角形A1B1C1;(2)三角形A1B1C1的顶点A1的坐标为　　　　,顶点C1的坐标为　　　　; (3)求三角形A1B1C1的面积;(4)已知点P在x轴上,以点A1,C1,P为顶点的三角形的面积为,求点P的坐标.解:(1)三角形A1B1C1如图所示.(2)(0,3)　(4,0)(3)如图,过点A1,B1作平行于x轴的直线,过点C1作平行于y轴的直线,得正方形A1DEF,则=---=4×4-×2×4-×2×1-×4×3=5.(4)由题意设点P的坐标为(t,0),∵以A1,C1,P为顶点的三角形的面积为,∴×3×|t-4|=,∴t=3或t=5,∴点P的坐标为(3,0)或(5,0).7．[2022扬州江都区八校联考]如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a,b,c满足关系式+(b-3)2=0,(c-4)2≤0.(1)求a,b,c的值;(2)如果在第二象限内有一点P(-m,),请用含m的式子表示四边形ABOP的面积;(3)在(2)的条件下,是否存在点P,使四边形ABOP的面积与三角形ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.解:(1)由+(b-3)2=0,(c-4)2≤0,可得a-2=0,b-3=0,c-4=0,∴a=2,b=3,c=4.(2)由(1)知,a=2,b=3,∴A(0,2),B(3,0),∴OA=2,OB=3.∴S三角形ABO=×2×3=3,S三角形APO=×2×m=m,∴S四边形ABOP=S三角形ABO+S三角形APO=3+m.(3)由(1)知,a=2,b=3,c=4,∴A(0,2),B(3,0),C(3,4),∴BC=4,∴S三角形ABC=×4×3=6,∵四边形ABOP的面积与三角形ABC的面积相等,∴m+3=6,∴m=3,∴P(-3,).类型二　知面积，求坐标方法指导：将点的横、纵坐标转化为到已知线段的距离,利用已知图形的面积表示线段之间的数量关系,即可求解.【例2】如图在平面直角坐标系中，A(1，2)，B(3，1)，点P在x轴负半轴，S△PAB＝3，求点P的坐标．分析：过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D，设点P(x，0)，利用S△PAB＝S△PAC＋S梯形ABDC－S△PBD，列出方程即可求出x的值．解：过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D，设点P(x，0)，∵A(1，2)，B(3，1)，∴PC＝1－x，PD＝3－x，AC＝2，BD＝1，CD＝2，∴S△PAB＝S△PAC＋S梯形ABDC－S△PBD∴3＝(1－x)×2＋－×(3－x)×1，解得x＝－1，则点P的坐标为(－1，0)【对应训练】8．如图，A(－1，0)，C(1，4)，点B在x轴上，且AB＝4.(1)点B的坐标为____________________；(2)△ABC的面积为________；(3)点P在y轴上，且以A，B，P三点为顶点的三角形的面积为12，则点P的坐标为___________________ .【答案】(3，0)或(－5，0)    8    (0，6)或(0，－6)9．如图，在平面直角坐标系中，已知点A(0，3)，B(2，1)，C(3，4).(1)请在图中画出△ABC；(2)△ABC的面积为________；(3)若点P在x轴上，且△OCP的面积为△ABC面积的1.5倍，求点P的坐标．解：(1)如图所示，△ABC即为所求　(2)4(3)由(2)得S△OCP＝4×1.5＝6.则有×4×OP＝6，∴OP＝3；当点P在x轴的负半轴上时，P(－3，0)；点P在x轴正半轴上时，P(3，0).∴点P的坐标为(－3，0)或(3，0)10．如图，在平面直角坐标系中，A(a，0)，C(b，2)，且满足(a＋2)2＋＝0，过C作CB⊥x轴于B.(1)求△ABC的面积；(2)在y轴上是否存在点P，使得△ABC和△ACP的面积相等？若存在，求出P点坐标；若不存在，请说明理由． 解：(1)∵(a＋2)2＋＝0，∴a＋2＝0，b－2＝0，∴a＝－2，b＝2，∵CB⊥AB，∴A(－2，0)，B(2，0)，C(2，2)，∴S△ABC＝×2×4＝4　(2)①当P在y轴正半轴上时，如图，设P(0，t)，过P作MN∥x轴，AN∥y轴，BM∥y轴，∵S△APC＝S梯形MNAC－S△ANP－S△CMP＝4，∴－t－(t－2)＝4，解得t＝3；②当P在y轴负半轴上时，如图，∵S△APC＝S梯形MNAC－S△ANP－S△CMP＝4，∴＋t－(2－t)＝4，解得t＝－1，∴P点坐标为(0，－1)或(0，3)