人教版数学七年级下册阶段测试2(5.3~5.4)
展开阶段测试2(5.3~5.4)
(时间:40分钟 满分:100分)
一、选择题(每小题6分,共36分)
1.下列现象属于平移的是 ( )
A.翻开书中的每一页纸张 B.飞碟的快速转动
C.电梯的上下移动 D.将一张纸沿它的中线折叠
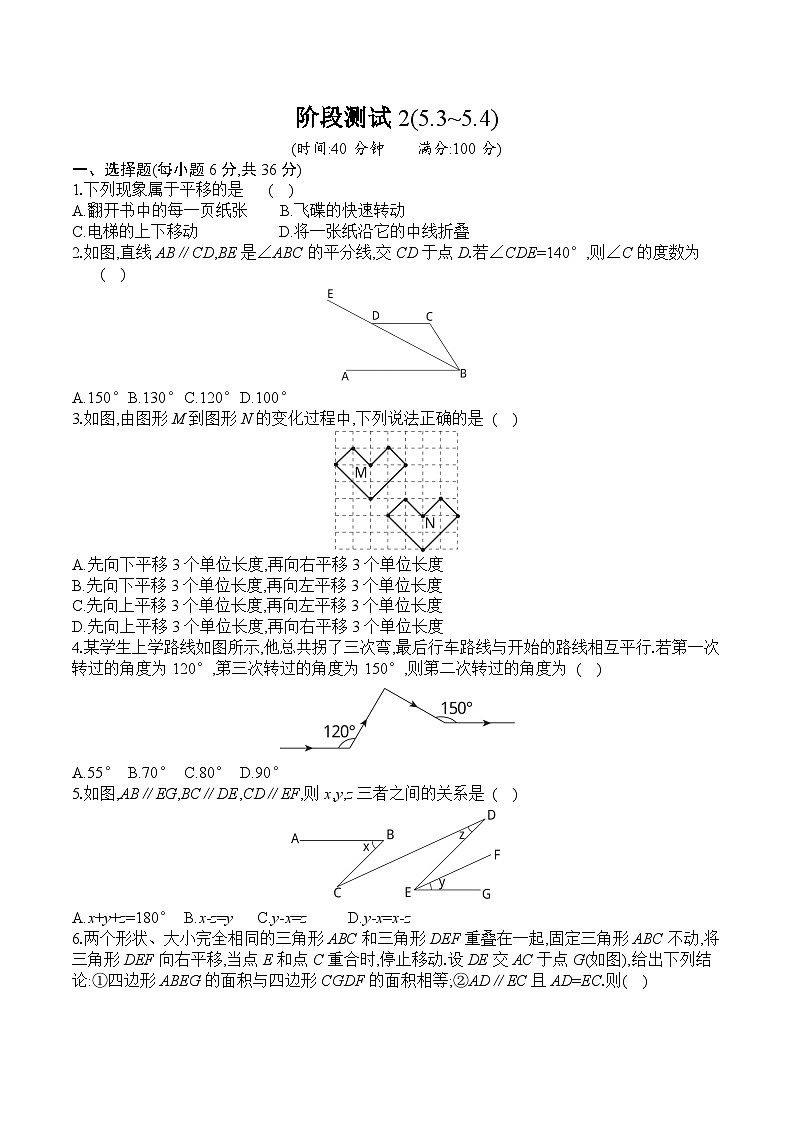
2.如图,直线AB∥CD,BE是∠ABC的平分线,交CD于点D.若∠CDE=140°,则∠C的度数为 ( )
A.150° B.130° C.120° D.100°
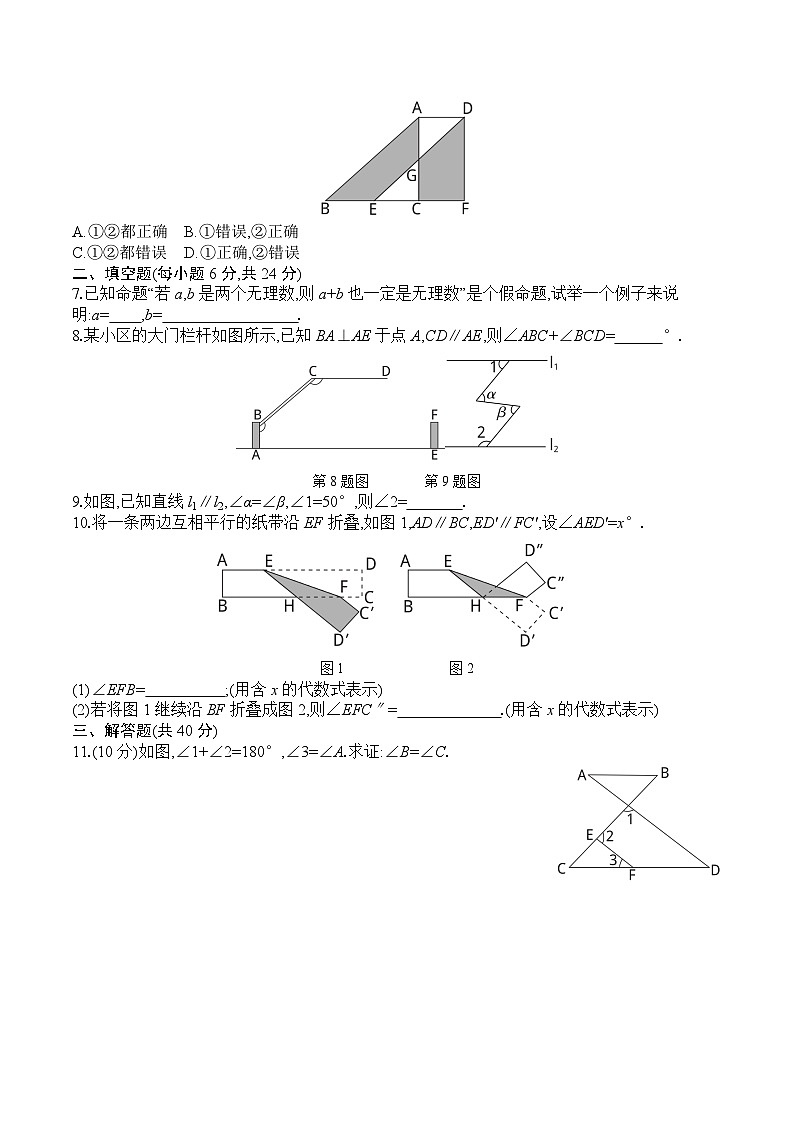
3.如图,由图形M到图形N的变化过程中,下列说法正确的是 ( )
A.先向下平移3个单位长度,再向右平移3个单位长度
B.先向下平移3个单位长度,再向左平移3个单位长度
C.先向上平移3个单位长度,再向左平移3个单位长度
D.先向上平移3个单位长度,再向右平移3个单位长度
4.某学生上学路线如图所示,他总共拐了三次弯,最后行车路线与开始的路线相互平行.若第一次转过的角度为120°,第三次转过的角度为150°,则第二次转过的角度为 ( )
A.55° B.70° C.80° D.90°
5.如图,AB∥EG,BC∥DE,CD∥EF,则x,y,z三者之间的关系是 ( )
A.x+y+z=180° B.x-z=y C.y-x=z D.y-x=x-z
6.两个形状、大小完全相同的三角形ABC和三角形DEF重叠在一起,固定三角形ABC不动,将三角形DEF向右平移,当点E和点C重合时,停止移动.设DE交AC于点G(如图),给出下列结论:①四边形ABEG的面积与四边形CGDF的面积相等;②AD∥EC且AD=EC.则( )
A.①②都正确 B.①错误,②正确
C.①②都错误 D.①正确,②错误
二、填空题(每小题6分,共24分)
7.已知命题“若a,b是两个无理数,则a+b也一定是无理数”是个假命题,试举一个例子来说明:a= ,b= .
8.某小区的大门栏杆如图所示,已知BA⊥AE于点A,CD∥AE,则∠ABC+∠BCD= °.
第8题图 第9题图
9.如图,已知直线l1∥l2,∠α=∠β,∠1=50°,则∠2= .
10.将一条两边互相平行的纸带沿EF折叠,如图1,AD∥BC,ED'∥FC',设∠AED'=x°.
图1 图2
(1)∠EFB= ;(用含x的代数式表示)
(2)若将图1继续沿BF折叠成图2,则∠EFC″= .(用含x的代数式表示)
三、解答题(共40分)
11.(10分)如图,∠1+∠2=180°,∠3=∠A.求证:∠B=∠C.
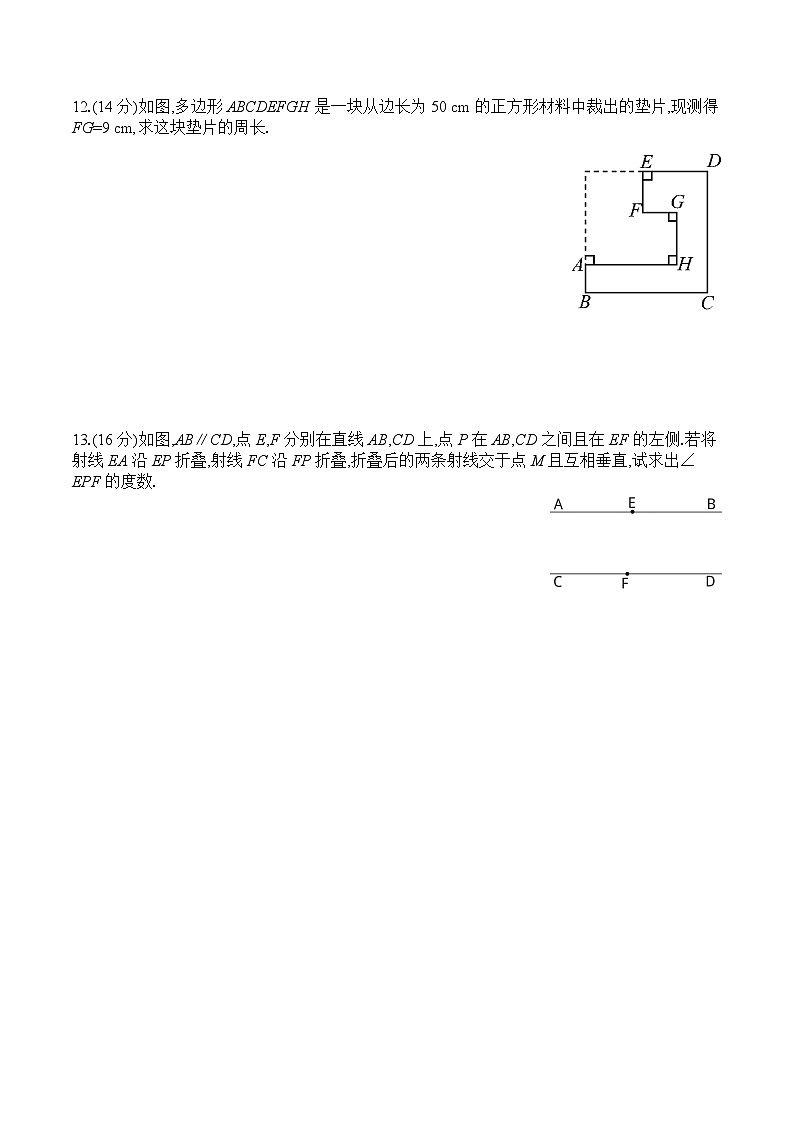
12.(14分)如图,多边形ABCDEFGH是一块从边长为50 cm的正方形材料中裁出的垫片,现测得FG=9 cm,求这块垫片的周长.
13.(16分)如图,AB∥CD,点E,F分别在直线AB,CD上,点P在AB,CD之间且在EF的左侧.若将射线EA沿EP折叠,射线FC沿FP折叠,折叠后的两条射线交于点M且互相垂直,试求出∠EPF的度数.
参考答案
一、选择题(每小题6分,共36分)
1.下列现象属于平移的是 (C)
A.翻开书中的每一页纸张
B.飞碟的快速转动
C.电梯的上下移动
D.将一张纸沿它的中线折叠
2.如图,直线AB∥CD,BE是∠ABC的平分线,交CD于点D.若∠CDE=140°,则∠C的度数为 (D)
A.150° B.130° C.120° D.100°
3.如图,由图形M到图形N的变化过程中,下列说法正确的是 (A)
A.先向下平移3个单位长度,再向右平移3个单位长度
B.先向下平移3个单位长度,再向左平移3个单位长度
C.先向上平移3个单位长度,再向左平移3个单位长度
D.先向上平移3个单位长度,再向右平移3个单位长度
4.某学生上学路线如图所示,他总共拐了三次弯,最后行车路线与开始的路线相互平行.若第一次转过的角度为120°,第三次转过的角度为150°,则第二次转过的角度为 (D)
A.55° B.70° C.80° D.90°
5.如图,AB∥EG,BC∥DE,CD∥EF,则x,y,z三者之间的关系是 (B)
A.x+y+z=180°
B.x-z=y
C.y-x=z
D.y-x=x-z
6.两个形状、大小完全相同的三角形ABC和三角形DEF重叠在一起,固定三角形ABC不动,将三角形DEF向右平移,当点E和点C重合时,停止移动.设DE交AC于点G(如图),给出下列结论:①四边形ABEG的面积与四边形CGDF的面积相等;②AD∥EC且AD=EC.则(D)
A.①②都正确 B.①错误,②正确
C.①②都错误 D.①正确,②错误
二、填空题(每小题6分,共24分)
7.已知命题“若a,b是两个无理数,则a+b也一定是无理数”是个假命题,试举一个例子来说明:a= ,b= -(本题答案不唯一) .
8.某小区的大门栏杆如图所示,已知BA⊥AE于点A,CD∥AE,则∠ABC+∠BCD= 270 °.
第8题图 第9题图
9.如图,已知直线l1∥l2,∠α=∠β,∠1=50°,则∠2= 130° .
10.将一条两边互相平行的纸带沿EF折叠,如图1,AD∥BC,ED'∥FC',设∠AED'=x°.
图1 图2
(1)∠EFB= 90°-x° ;(用含x的代数式表示)
(2)若将图1继续沿BF折叠成图2,则∠EFC″= x°-90° .(用含x的代数式表示)
三、解答题(共40分)
11.(10分)如图,∠1+∠2=180°,∠3=∠A.求证:∠B=∠C.
证明:∵∠1+∠2=180°,∴AD∥EF,
∴∠3=∠D.又∵∠3=∠A,∴∠A=∠D,
∴AB∥CD,∴∠B=∠C.
12.(14分)如图,多边形ABCDEFGH是一块从边长为50 cm的正方形材料中裁出的垫片,现测得FG=9 cm,求这块垫片的周长.
解:这块垫片的周长是218 cm.
13.(16分)如图,AB∥CD,点E,F分别在直线AB,CD上,点P在AB,CD之间且在EF的左侧.若将射线EA沿EP折叠,射线FC沿FP折叠,折叠后的两条射线交于点M且互相垂直,试求出∠EPF的度数.
解:①如图1,过点M作MN∥AB.
∵AB∥CD,∴AB∥CD∥MN,
∴∠AEM=∠EMN,∠NMF=∠CFM.
∵∠EMF=90°,∴∠AEM+∠CFM=90°.
同理可得∠EPF=∠AEP+∠CFP.
由折叠可得∠AEP=∠PEM=∠AEM,∠PFC=∠PFM=∠CFM,
∴∠EPF=(∠AEM+∠CFM)=45°.
②如图2,过点M作MN∥AB.
∵AB∥CD,∴AB∥CD∥MN,
∴∠AEM+∠EMN=180°,∠NMF+∠CFM=180°,
∴∠AEM+∠EMF+∠CFM=360°.
∵∠EMF=90°,∴∠AEM+∠CFM=270°.
由折叠可得∠AEP=∠PEM=∠AEM,∠PFC=∠PFM=∠CFM,
∴∠EPF=(∠AEM+∠CFM)=×270°=135°.
综上所述,∠EPF的度数为45°或135°.
图1 图2









