2023年江苏省镇江市丹阳市中考数学模拟试卷(含答案)

这是一份2023年江苏省镇江市丹阳市中考数学模拟试卷(含答案)，共29页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2023年江苏省镇江市丹阳市中考数学模拟试卷
一、选择题（本大题共6小题，共18.0分。在每小题列出的选项中，选出符合题目的一项）
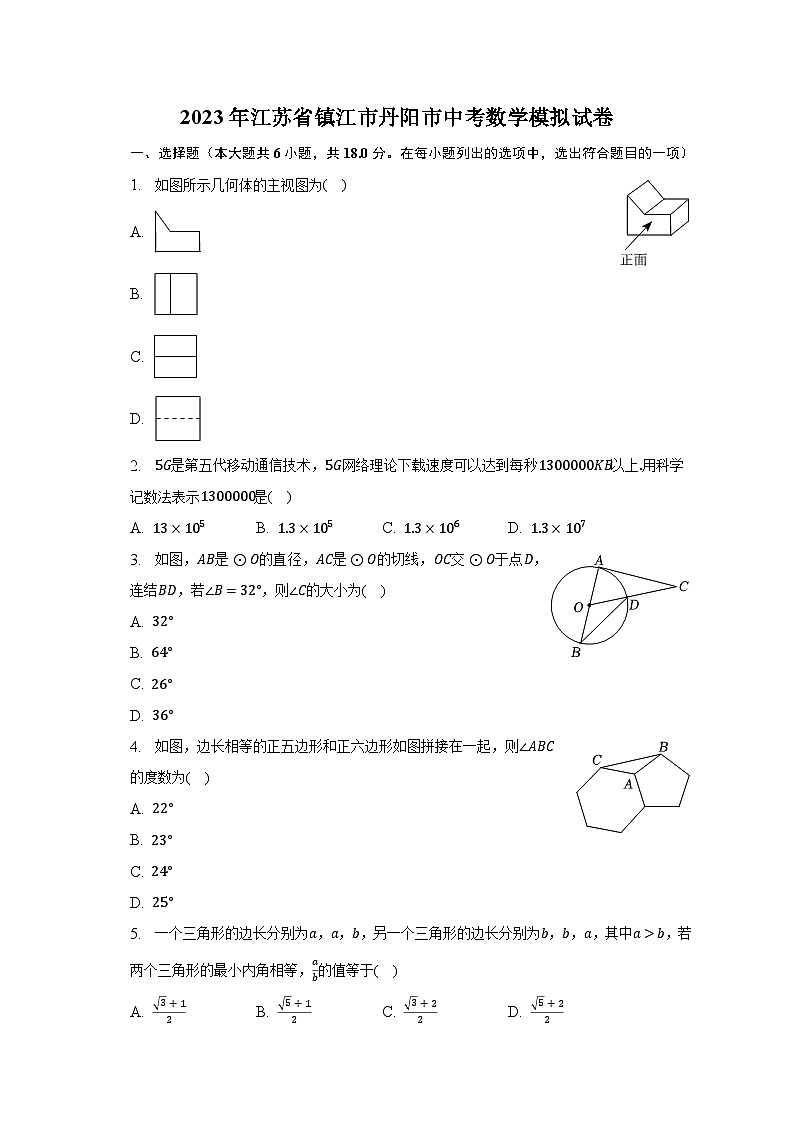
1. 如图所示几何体的主视图为(    )
A.
B.
C.
D.
2. 5G是第五代移动通信技术，5G网络理论下载速度可以达到每秒1300000KB以上.用科学记数法表示1300000是(    )
A. 13×105 B. 1.3×105 C. 1.3×106 D. 1.3×107
3. 如图，AB是⊙O的直径，AC是⊙O的切线，OC交⊙O于点D，连结BD，若∠B=32°，则∠C的大小为(    )
A. 32°
B. 64°
C. 26°
D. 36°
4. 如图，边长相等的正五边形和正六边形如图拼接在一起，则∠ABC的度数为(    )
A. 22°
B. 23°
C. 24°
D. 25°
5. 一个三角形的边长分别为a，a，b，另一个三角形的边长分别为b，b，a，其中a>b，若两个三角形的最小内角相等，ab的值等于(    )
A. 3+12 B. 5+12 C. 3+22 D. 5+22
6. 若二次函数y=ax2+4ax+1(a≠0)的图象经过(-3- 2,y1)、(-1+ 2,y2)、(1,y3)、(2,y4)，若y1、y2、y3、y4四个数中有且只有一个小于零，则a的值可以是(    )
A. 110 B. 14 C. -110 D. -14
二、填空题（本大题共12小题，共24.0分）
7. -2023的绝对值是            ．
8. 二次根式 x-1有意义的条件是          ．
9. 如图，五边形ABCDE中，∠A=125°，则∠1+∠2+∠3+∠4的度数是______．


10. 为了践行“首都市民卫生健康公约”，某班级举办“七步洗手法”比赛活动，小明的单项成绩如表所示(各项成绩均按百分制计)：
项目
书面测试
实际操作
宣传展示
成绩(分)
96
98
96
若按书面测试占30%、实际操作占50%、宣传展示占20%，计算参赛个人的综合成绩(百分制)，则小明的最后得分是______．
11. 实数-64的立方根是______ ．
12. 一元二次方程x(x-5)=0的根为______．
13. 如图，已知△ABC∽△AMN，点M是AC的中点，AB=6，AC=8，则AN=______．


14. 请写出一个图象经过点(1,3)的一次函数表达式______ ．
15. 为了落实“双减”政策，武汉市某学校对初中学生的课外作业时长进行了问卷调查，15名同学的作业时长统计如下表，则这组数据的众数是        分钟．
作业时长(单位：分钟)
50
60
70
80
90
人数(单位：人)
2
4
6
2

1

16. 把三张形状、大小相同但画面不同的风景图片，都按同样的方式剪成相同三段，然后将上、中、下三段分别混合洗匀，从三堆图片中随机地各抽出一张，这三张图片恰好组成一张完整风景图片的概率为______ ．
17. 如图是由边长为1的小正方形构成的6×7的网格，已知点A，B，C，D均在格点上，且点C，D不重合，∠ABC=∠ABD=45°，AB=4，AC=AD= 10，则CD长为        ．


18. 如图，在平面直角坐标系中，矩形ABCD的边AB=4，BC=6.若不改变矩形ABCD的形状和大小，当矩形顶点A在x轴的正半轴上左右移动时，矩形的另一个顶点D始终在y轴的正半轴上随之上下移动.当点A移动到某一位置时，点C到点O的距离有最大值，则此时点A的横坐标为______ ．
三、解答题（本大题共10小题，共78.0分。解答应写出文字说明，证明过程或演算步骤）
19. (本小题8.0分)
(1)计算：(4-π)0+(13)-1-2cos45°；
(2)化简：(1+1x-1)+xx2-1．
20. (本小题10.0分)
(1)解方程：2x-1+11-x=13．
(2)解不等式组13(x+1)≤1x+22≥x+33．
21. (本小题6.0分)
如图，四边形ABCD为平行四边形，E为AD上的一点，连接EB并延长，使BF=BE，连接EC并延长，使CG=CE，连接FG.H为FG的中点，连接DH．
(1)求证：四边形AFHD为平行四边形；
(2)若CB=CE，∠BAE=80°，∠DCE=30°，求∠CBE的度数．

22. (本小题6.0分)
某校为创建书香校园，倡导读书风尚，开展了师生“大阅读”活动，并制定“大阅读”星级评选方案，每月评选一次，为了解活动开展情况，学校组织对全校八年级“大阅读”星级评选工作进行抽样调查，随机抽取20名学生阅读的积分(分值为整数)情况进行分析．
【收集数据】20名学生的“大阅读”积分(单位：分)：32，43，34，35，15，46，48，24，54，10，25，40，60，42，55，30，47，28，37，42
【整理数据】
积分/分
10≤x≤19
20k2x的取值范围；
(3)求△ABO的面积；
(4)点P在x轴上，当△PAO为等腰三角形，请直接写出点P的坐标．

26. (本小题8.0分)
阅读与思考下面是小颖的数学日记，请仔细阅读，并完成相应的任务．
×年×月×日星期六
在圆中只用无刻度的直尺作出满足某条件的圆周角
今天在数学课上，我学会了在圆中只用无刻度的直尺就可以作出满足某条件的圆周角．
问题一：如图1，∠BAC是⊙O的圆周角，我们可以在⊙O中只用无刻度的直尺作一个圆周角等于∠BAC.作法：在⊙O上取一点D，连接BD和CD，则∠D=∠A(依据*)．

问题二：在图1的基础上，要在⊙O中只用无刻度的直尺以B为顶点作与∠A相等的圆周角，应该如何完成呢？
作法：如图2所示，连接CO并延长，交⊙O于点D，连接BD，连接BO并延长，交⊙O于点E，则∠DBE即为所要求作的角．

问题三：如图3，要在⊙O中只用无刻度的直尺作一个圆周角与∠A互余，应该如何完成呢？

……
任务：
(1)“问题一”中小颖的“依据*”是指        ；
(2)请说明“问题二”中小颖的作法是否正确并说明理由；
(3)完成“问题三”：请在图3中只用无刻度的直尺作出满足条件的圆周角，并仿照“问题二”写出具体作法．
27. (本小题11.0分)
在学习了“中心对称图形…平行四边形”这一章后，同学小明对特殊四边形的探究产生了浓厚的兴趣，他发现除了已经学过的特殊四边形外，还有很多比较特殊的四边形，勇于创新的他大胆地作出这样的定义：有一个内角是直角，且对角线互相垂直的四边形称为“双直四边形”.请你根据以上定义，回答下列问题：

(1)下列关于“双直四边形”的说法，正确的有______ (把所有正确的序号都填上)；
①双直四边形”的对角线不可能相等：
②“双直四边形”的面积等于对角线乘积的一半；
③若一个“双直四边形”是中心对称图形，则其一定是正方形．
(2)如图①，正方形ABCD中，点E、F分别在边AB、AD上，连接CE，BF，EF，CF，若AE=DF，证明：四边形BCFE为“双直四边形”；
(3)如图②，在平面直角坐标系中，已知点A(0,6)，C(8,0)，点B在线段OC上且AB=BC，是否存在点D在第一象限，使得四边形ABCD为“双直四边形”，若存在；求出所有点D的坐标，若不存在，请说明理由．
28. (本小题11.0分)
如图，某跳水运动员进行10米跳台跳水训练，水面边缘点E的坐标为(-32,-10)，运动员(将运动员石成一点)在空中运动的路线是经过原点O的抛物线，在跳某个规定动作时，运动员在空中最高处A点的坐标为(1,54)，正常情况下，运动员在距水面高度5米以前．
必须完成规定的翻腾，打开动作，并调整好入水姿势，否别就会失误，运动员入水后，运动路线为另一条抛物线．
(1)求运动员在空中运动时对应抛物线的解析式并求出入水处B点的坐标；
(2)若运动员在空中调整好入水姿势时，恰好距点E的水平距离为5米，问该运动员此次跳水会不会失误？通过计算说明理由；
(3)在该运动员入水点的正前方有M，N两点，且EM=212，EN=272，该运动员入水后运动路线对应的抛物线解析式为y=a(x-h)2+k，且顶点C距水面4米，若该运动员出水点D在MN之间(包括M，N两点)，求h的取值范围．


答案和解析

1.【答案】A 
【解析】解：观察图形可知，该几何体的主视图如下：

故选：A．
找到从正面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中．
本题考查了简单组合体的三视图，主视图是从物体的正面看得到的视图．

2.【答案】C 
【解析】解：1300000=1.3×106，
故选：C．
科学记数法的表示形式为a×10n的形式，其中1≤|a|