2023年中考数学压轴题专项训练 专题27以相似为载体的几何综合问题（试题+答案）

这是一份2023年中考数学压轴题专项训练 专题27以相似为载体的几何综合问题（试题+答案），文件包含2023年中考数学压轴题专项训练专题27以相似为载体的几何综合问题答案docx、2023年中考数学压轴题专项训练专题27以相似为载体的几何综合问题试题docx等2份试卷配套教学资源，其中试卷共82页， 欢迎下载使用。
挑战2023年中考数学压轴题之学霸秘笈大揭秘（全国通用）
专题27以相似为载体的几何综合问题

21．（2022·四川内江·中考真题）如图，在矩形ABCD中，AB＝6，BC＝4，点M、N分别在AB、AD上，且MN⊥MC，点E为CD的中点，连接BE交MC于点F．

(1)当F为BE的中点时，求证：AM＝CE；
(2)若EFBF＝2，求ANND的值；
(3)若MN∥BE，求ANND的值．
【答案】(1)见解析
(2)2737
(3)27

【分析】(1)根据矩形的性质，证明△BMF≌ △ECF，得BM＝CE，再利用点E为CD的 中点，即可证明结论；
(2)利用△BMF∽△ECF，得BFEF=BMCE=12，从而求出BM的长，再利用△ANM∽△BMC ，得ANBM=AMBC ，求出AN的长，可得答案；
(3)首先利用同角的余角相等得 ∠CBF＝ ∠CMB，则tan∠CBF＝tan∠CMB，得CEBC=BCBM ，可得BM的长，由（2）同理可得答案．
（1）
证明：∵F为BE的中点，
∴BF＝EF，
∵四边形ABCD是矩形，
∴AB∥CD，AB＝CD
∴∠BMF＝∠ECF，
∵∠BFM＝∠EFC，
∴△BMF≌△ECF（AAS），
∴BM＝CE，
∵点E为CD的中点，
∴CE＝12CD，
∵AB＝CD，
∴BM=CE=12AB，
∴AM=BM，
∴AM＝CE；
（2）
∵∠BMF＝∠ECF，∠BFM＝∠EFC，
∴△BMF∽△ECF，
∴BFEF=BMCE=12，
∵CE＝3，
∴BM＝32，
∴AM＝92，
∵CM⊥MN，
∴∠CMN＝90°，
∴∠AMN+∠BMC＝90°，
∵∠AMN+∠ANM＝90°，
∴∠ANM＝∠BMC，
∵∠A＝∠MBC，
∴△ANM∽△BMC，
∴ANBM=AMBC，
∴AN32=924，
∴AN=2716，
∴DN＝AD﹣AN＝4﹣2716＝3716，
∴ANDN=27163716=2737；
（3）
∵MN∥BE，
∴∠BFC＝∠CMN，
∴∠FBC+∠BCM＝90°，
∵∠BCM+∠BMC＝90°，
∴∠CBF＝∠CMB，
∴tan∠CBF＝tan∠CMB，
∴CEBC=BCBM，
∴34=4BM，
∴BM=163，
∴AM=AB−BM=6−163=23，
由（2）同理得，ANBM=AMBC，
∴AN163=234，
解得：AN＝89，
∴DN＝AD﹣AN＝4﹣89＝289，
∴ANND=89289=27．
【点睛】本题是相似形综合题，主要考查了矩形的性质，全等三角形的判定与性质，相似三角形的判定与性质，三角函数等知识，求出BM的长是解决（2）和（3）的关键．
22．（2022·贵州铜仁·中考真题）如图，在四边形ABCD中，对角线AC与BD相交于点O，记△COD的面积为S1，△AOB的面积为S2．
（1）问题解决：如图①，若AB//CD，求证：S1S2=OC⋅ODOA⋅OB
（2）探索推广：如图②，若AB与CD不平行，（1）中的结论是否成立？若成立，请证明；若不成立，请说明理由．
（3）拓展应用：如图③，在OA上取一点E，使OE=OC，过点E作EF∥CD交OD于点F，点H为AB的中点，OH交EF于点G，且OG=2GH，若OEOA=56，求S1S2值．

【答案】（1）见解析；（2）（1）中的结论成立，理由见解析：（3）2554
【分析】（1）如图所示，过点D作AE⊥AC于E，过点B作BF⊥AC于F，求出DE=OD⋅sin∠DOE，BF=OB⋅sin∠BOF，然后根据三角形面积公式求解即可；
（2）同（1）求解即可；
（3）如图所示，过点A作AM∥EF交OB于M，取BM中点N，连接HN，先证明△OEF≌△OCD，得到OD=OF，证明△OEF∽△OAM，得到OFOM=OEOA=56，设OE=OC=5m，OF=OD=5n，则OA=6m，OM=6n，证明△OGF∽△OHN，推出ON=32OF=15n2，BN=MN=ON−OM=3n2，则OB=ON+BN=9n，由（2）结论求解即可．
【详解】解：（1）如图所示，过点D作AE⊥AC于E，过点B作BF⊥AC于F，
∴DE=OD⋅sin∠DOE，BF=OB⋅sin∠BOF，
∴S△OCD=S1=12OC⋅DE=12OC⋅OD⋅sin∠DOE，
S△AOB=S2=12OA⋅BF=12OA⋅OB⋅sin∠BOF，
∵∠DOE=∠BOF，
∴sin∠DOE=sin∠BOF；
∴S1S2=12OC⋅OD⋅sin∠DOE12OA⋅OB⋅sin∠BOF=OC⋅ODOA⋅OB；

（2）（1）中的结论成立，理由如下：
如图所示，过点D作AE⊥AC于E，过点B作BF⊥AC于F，
∴DE=OD⋅sin∠DOE，BF=OB⋅sin∠BOF，
∴S△OCD=S1=12OC⋅DE=12OC⋅OD⋅sin∠DOE，
S△AOB=S2=12OA⋅BF=12OA⋅OB⋅sin∠BOF，
∵∠DOE=∠BOF，
∴sin∠DOE=sin∠BOF；
∴S1S2=12OC⋅OD⋅sin∠DOE12OA⋅OB⋅sin∠BOF=OC⋅ODOA⋅OB；

（3）如图所示，过点A作AM∥EF交OB于M，取BM中点N，连接HN，
∵EF∥CD，
∴∠ODC=∠OFE，∠OCD=∠OEF，
又∵OE=OC，
∴△OEF≌△OCD（AAS），
∴OD=OF，
∵EF∥AM，
∴△OEF∽△OAM，
∴OFOM=OEOA=56，
设OE=OC=5m，OF=OD=5n，则OA=6m，OM=6n，
∵H是AB的中点，N是BM的中点，
∴HN是△ABM的中位线，
∴HN∥AM∥EF，
∴△OGF∽△OHN，
∴OGOH=OFON，
∵OG=2GH，
∴OG=23OH，
∴OGOH=OFON=23，
∴ON=32OF=15n2，BN=MN=ON−OM=3n2，
∴OB=ON+BN=9n，
由（2）可知S1S2=OC⋅ODOA⋅OB=5m⋅5n6m⋅9n=2554．

【点睛】本题主要考查了解直角三角形，相似三角形的性质与判定，全等三角形的性质与判定，三角形中位线定理，正确作出辅助线是解题的关键．
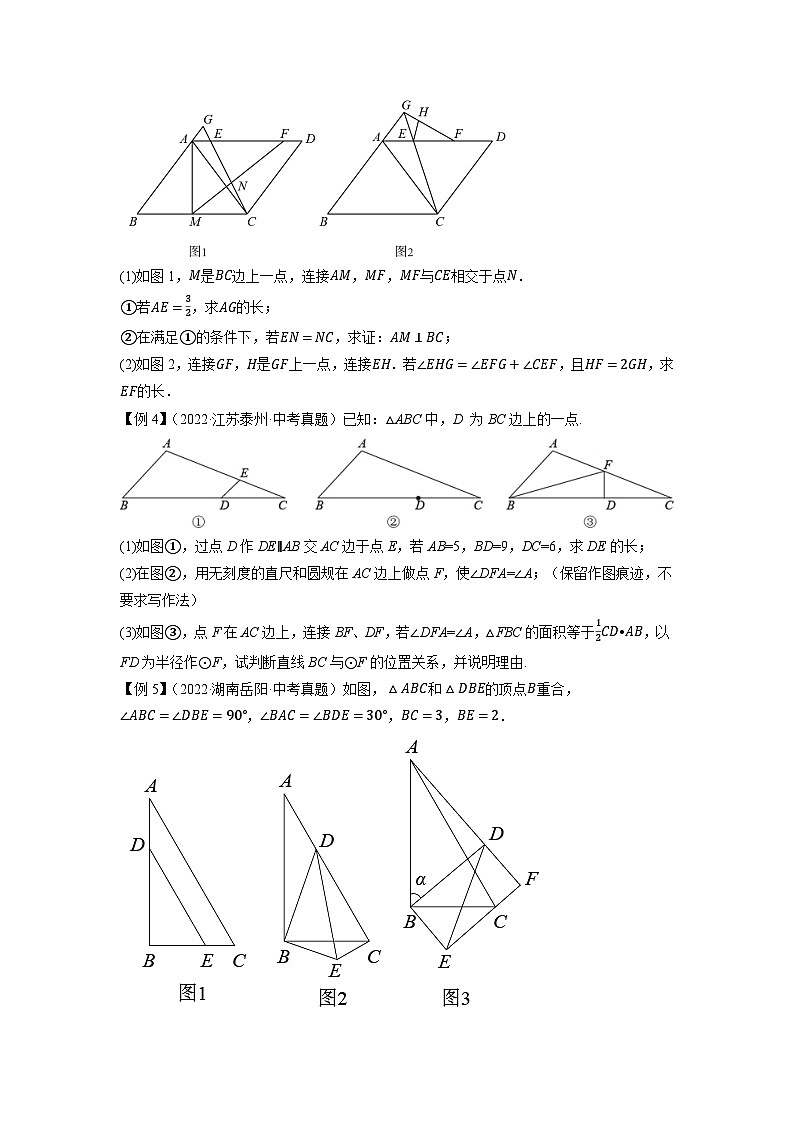
23．（2022·内蒙古包头·中考真题）如图，在平行四边形ABCD中，AC是一条对角线，且AB=AC=5，BC=6，E，F是AD边上两点，点F在点E的右侧，AE=DF，连接CE，CE的延长线与BA的延长线相交于点G．

(1)如图1，M是BC边上一点，连接AM，MF，MF与CE相交于点N．
①若AE=32，求AG的长；
②在满足①的条件下，若EN=NC，求证：AM⊥BC；
(2)如图2，连接GF，H是GF上一点，连接EH．若∠EHG=∠EFG+∠CEF，且HF=2GH，求EF的长．
【答案】(1)①53；②证明见解析
(2)2

【分析】（1）①解：根据平行四边形ABCD的性质可证△AGE∽△DCE，得到AGDC=AEDE，再根据AB=AC=5，BC=6，AE=32，结合平行四边形的性质求出DE的长，代入比例式即可求出AG的长；
②先根据ASA证明△ENF≌△CNM可得EF=CM，再根据AE=32，AE=DF求出EF=3，进一步证明BM=MC，最后利用等腰三角形的三线合一可证明结论．
（2）如图，连接CF，先根据SAS证明△AEC≌△DFC，再结合∠EHG=∠EFG+∠CEF，说明EH∥CF，利用平行线分线段成比例定理可得GEEC=12，接着证明△AGE∽△DCE，可得到AEDE=12，设AE=x，则DE=2x，根据AD=AE+DE=6构建方程求出x，最后利用EF=AD−AE−DF可得结论．
（1）
①解：如图，
∵四边形ABCD是平行四边形，AB=AC=5，BC=6，
∴AB∥CD，AD∥BC，DC=AB=5，AD=BC=6，
∴∠GAE=∠CDE，∠AGE=∠DCE，
∴△AGE∽△DCE，
∴AGDC=AEDE，
∴AG·DE=DC·AE，
∵AE=32，
∴DE=AD−AE=6−32=92，
∴92AG=5×32，
∴AG=53，
∴AG的长为53．

②证明：∵AD∥BC，
∴∠EFN=∠CMN，
∵EN=NC，
在△ENF和△CNM中，
∠EFN=∠CMNEN=CN∠ENF=∠CNM
∴△ENF≌△CNMASA，
∴EF=CM，
∵AE=32，AE=DF，
∴DF=32，
∴EF=AD−AE−DF=3，
∴CM=3，
∵BC=6，
∴BM=BC−CM=3，
∴BM=MC，
∵AB=AC，
∴AM⊥BC．
（2）
如图，连接CF，
∵AB=AC，AB=DC，
∴AC=DC，
∴∠CAD=∠CDA，
∵AE=DF，
在△AEC和△DFC中，
AC=DC∠CAD=∠CDAAE=DF
∴△AEC≌△DFCSAS，
∴CE=CF，
∴∠CFE=∠CEF
∵∠EHG=∠EFG+∠CEF，
∴∠EHG=∠EFG+∠CEF=∠EFG+∠CFE=∠CFG，
∴EH∥CF，
∴GHHF=GEEC，
∵HF=2GH，
∴GEEC=12，
∵AB∥CD，
∴∠GAE=∠CDE，∠AGE=∠DCE，
∴△AGE∽△DCE，
∴AEDE=GECE，
∴AEDE=12，
∴DE=2AE，
设AE=x，则DE=2x，
∵AD=6，
∴AD=AE+DE=x+2x=6，
∴x=2，
即AE=2，
∴DF=2，
∴EF=AD−AE−DF=2．
∴EF的长为2．

【点睛】本题考查了平行四边形的性质，相似三角形的判定及性质，全等三角形的判定及性质，等腰三角形的三线合一，平行线的判定及性质，平行线分线段成比例定理等知识．灵活运用相似三角形和全等三角形的判定及性质是解答本题的关键．
24．（2022·江苏泰州·中考真题）已知：△ABC中，D 为BC边上的一点.

(1)如图①，过点D作DE∥AB交AC边于点E，若AB=5，BD=9，DC=6，求DE的长；
(2)在图②，用无刻度的直尺和圆规在AC边上做点F，使∠DFA=∠A；（保留作图痕迹，不要求写作法）
(3)如图③，点F在AC边上，连接BF、DF，若∠DFA=∠A，△FBC的面积等于12CD•AB，以FD为半径作⊙F，试判断直线BC与⊙F的位置关系，并说明理由.
【答案】(1)2
(2)图见详解
(3)直线BC与⊙F相切，理由见详解

【分析】（1）由题意易得CDBD=23，则有CDCB=25，然后根据相似三角形的性质与判定可进行求解；
（2）作DT∥AC交AB于点T，作∠TDF=∠ATD，射线DF交AC于点F，则点F即为所求；
（3）作BR∥CF交FD的延长线于点R，连接CR，证明四边形ABRF是等腰梯形，推出AB=FR，由CF∥BR，推出S△CFB=S△CFR=12AB⋅CD=12FR⋅CD，推出CD⊥DF，然后问题可求解．
（1）
解：∵DE∥AB，
∴△CDE∽△CBA，
∴DEAB=CDCB，
∵AB=5，BD=9，DC=6，
∴DE5=66+9，
∴DE=2；
（2）
解：作DT∥AC交AB于点T，作∠TDF=∠ATD，射线DF交AC于点F，则点F即为所求；
如图所示：点F即为所求，

（3）
解：直线BC与⊙F相切，理由如下：
作BR∥CF交FD的延长线于点R，连接CR，如图，

∵∠DFA=∠A，
∴四边形ABRF是等腰梯形，
∴AB=FR，
∵△FBC的面积等于12CD•AB，
∴S△CFB=S△CFR=12AB⋅CD=12FR⋅CD，
∴CD⊥DF，
∵FD是⊙F的半径，
∴直线BC与⊙F相切．
【点睛】本题主要考查相似三角形的性质与判定、平行线的性质与判定及切线的判定，熟练掌握相似三角形的性质与判定、平行线的性质与判定及切线的判定是解题的关键．
25．（2022·湖南岳阳·中考真题）如图，△ABC和△DBE的顶点B重合，∠ABC=∠DBE=90°，∠BAC=∠BDE=30°，BC=3，BE=2．

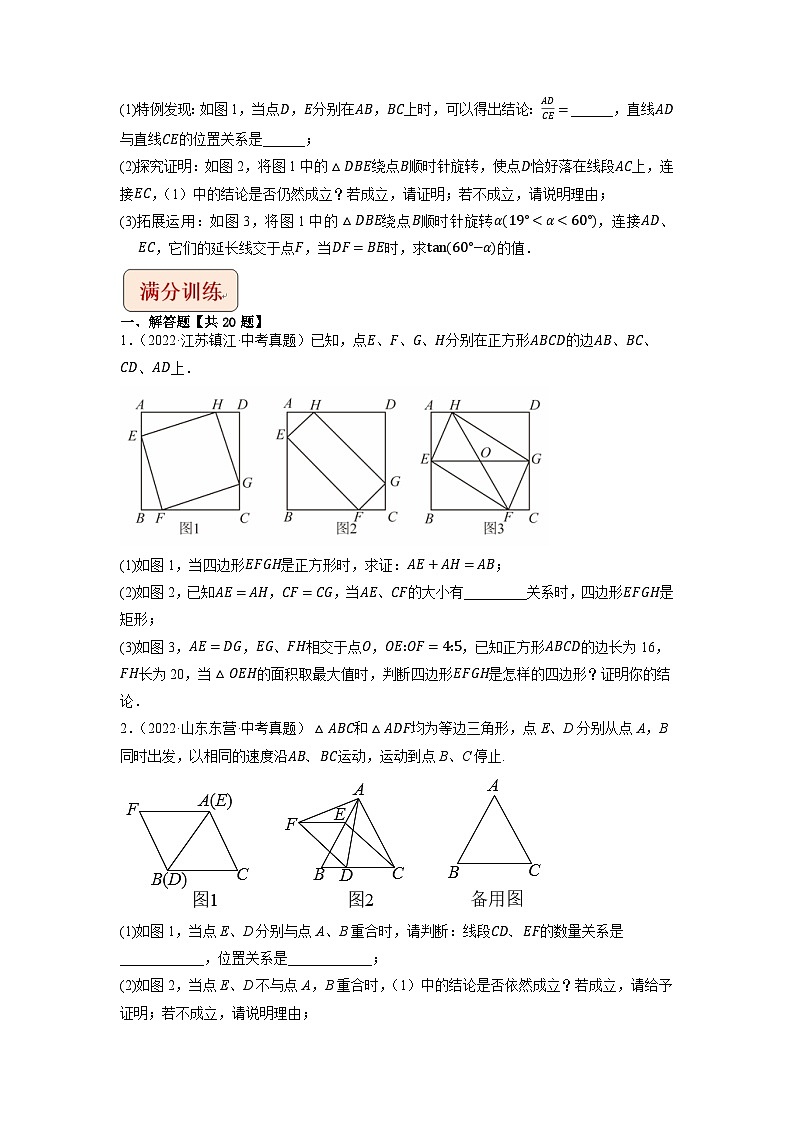
(1)特例发现：如图1，当点D，E分别在AB，BC上时，可以得出结论：ADCE=______，直线AD与直线CE的位置关系是______；
(2)探究证明：如图2，将图1中的△DBE绕点B顺时针旋转，使点D恰好落在线段AC上，连接EC，（1）中的结论是否仍然成立？若成立，请证明；若不成立，请说明理由；
(3)拓展运用：如图3，将图1中的△DBE绕点B顺时针旋转α(19°